Facharbeit Lernpfad Terme/Aufstellen und Interpretieren von Termen: Unterschied zwischen den Versionen
K (→Übungsaufgaben) |
K (→Übungsaufgaben) |
||
| Zeile 135: | Zeile 135: | ||
* A(15cm;13cm)= 4cm(15cm+13cm)= 4cm•28cm= 112cm<sup>2</sup> | * A(15cm;13cm)= 4cm(15cm+13cm)= 4cm•28cm= 112cm<sup>2</sup> | ||
</popup> </div> | </popup> </div> | ||
| + | |||
| + | |||
| + | |||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 4:</span>'''Laura hat zu schnell von der Tafel abgeschrieben. Dabei hat sie die Werte der Variablen vergessen, nur die Ergebnisse hat sie noch. Hilf ihr die passenden Werte für die Variablen zu finden, wenn der Term T(n)=n<sup>2</sup>+2 lautete. | ||
| + | Warum gibt es meist zwei Möglichkeiten? | ||
| + | |||
| + | a) T(?)= 18 | ||
| + | |||
| + | b) T(?)= 38 | ||
| + | |||
| + | c) T(?)= 3 | ||
| + | |||
| + | d) T(?)= 6 | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | Es gibt zwei Möglichkeiten, da ein Glied des Term n<sup>2</sup> lautet. Eine quadrierte Zahl ist immer positiv. (Bsp.: 3<sup>2</sup>=9=(-3)<sup>2</sup> ) | ||
| + | |||
| + | a) T(4)= T(-4)= 4<sup>2</sup>+2= 16+2= 18 | ||
| + | |||
| + | b) T(6)= T(-6)= 6<sup>2</sup>+2= 36+2= 38 | ||
| + | |||
| + | c) T(1)= T(-1)= 1<sup>2</sup>+2= 1+2= 3 | ||
| + | |||
| + | d) T(2)= T(-2)= 2<sup>2</sup>+2= 4+2= 6 | ||
Version vom 11. August 2010, 11:23 Uhr
Inhaltsverzeichnis |
Aufstellen und Interpretieren von Termen
Aufstellen von Termen
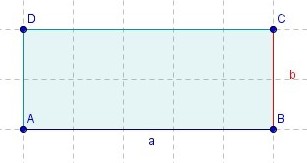
Übertrage die Zeichnung in dein Heft und überlege dir einen Term, mit dem du den Flächeninhalt ausrechnen kannst.
Setze nun für a=2cm und b=3cm ein
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Rezept
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
Interpretieren von Termen
|
|
Übungsaufgaben
a) Addiere 2 zum Quadrat von x
b) Addiere 6 zum vierfachen der Zahl n
c) Multipliziere die Summe aus b und der Zahl 7 mit 4
d) Multipliziere x mit seiner Gegenzahl
e) Multipliziere den Vorgänger der natürlichen Zahl n mit seinem Nachfolger
|
Warum gibt es meist zwei Möglichkeiten?
a) T(?)= 18
b) T(?)= 38
c) T(?)= 3
d) T(?)= 6
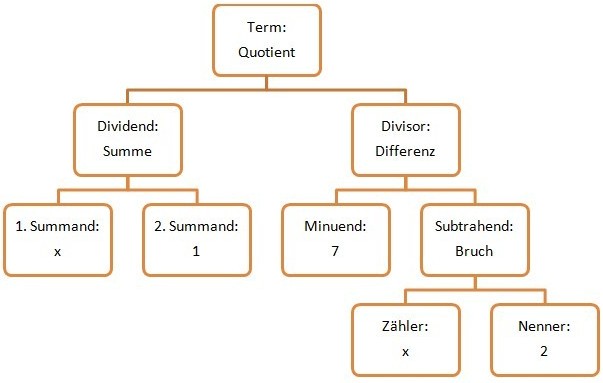
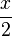 )
)
 ) = 5:(7-2) = 5:5 = 1
) = 5:(7-2) = 5:5 = 1
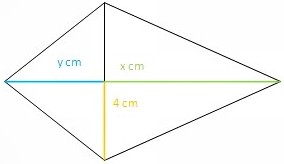

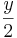 cm)+(8cm•
cm)+(8cm•
