Facharbeit Lernpfad Terme/Aufstellen und Interpretieren von Termen: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 40: | Zeile 40: | ||
''' <span style="color: blue"></span>''' <br /> | ''' <span style="color: blue"></span>''' <br /> | ||
{| | {| | ||
| − | ! width=" | + | ! width="600" | |
! width="10" | | ! width="10" | | ||
|- | |- | ||
| Zeile 91: | Zeile 91: | ||
| − | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 3:</span>''' Gib einen Term an, der den Flächeninhalt der abgebildeten Figur berechnet. Berechne anschließend den Flächeninhalt der Figur, indem du für die Variablen die angegebenen Zahlen einsetzt. | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 3:</span>''' |
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| | ||
| + | ! width="800" | | ||
| + | ! width="10" | | ||
| + | |- | ||
| + | | valign="top" | | ||
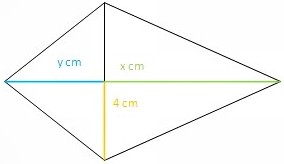
| + | <br /> <br /> Gib einen Term an, der den Flächeninhalt der abgebildeten Figur berechnet. | ||
| + | |||
| + | Berechne anschließend den Flächeninhalt der Figur, indem du für die Variablen die angegebenen Zahlen einsetzt. | ||
* A(8cm;2cm) | * A(8cm;2cm) | ||
| Zeile 97: | Zeile 109: | ||
* A(12cm;9cm) | * A(12cm;9cm) | ||
* A(15cm;13cm) | * A(15cm;13cm) | ||
| − | [[Bild:drachenviereck.jpg]] | + | |
| + | <u>Hinweis: Die Figur ist Achsensymmetrisch</u> | ||
| + | |} <br /> <br /> | ||
| + | | | ||
| + | | valign="top" | | ||
| + | [[Bild:drachenviereck.jpg]] <br /> <br /> | ||
| + | |} | ||
| + | <popup name="Lösung"> | ||
| + | Das Drachenviereck besteht aus 2 großen (wegen der Achsensymmetrie: gleichgroßen) Dreiecken. Deshalb kann man sich den Flächeninhalt eines dieser Dreiecke überlegen und ihn dann verdoppeln. Der Flächeninhalt eines Dreiecks ist allgemein: A<sub>D</sub> <math>\frac{1}{2}</math> <span style="color: darkblue">a</span>•<span style="color: darkorange">h<sub>a</sub> | ||
| + | </span> | ||
| + | |||
| + | In diesem Fall also: A<sub>D</sub> = <math>\frac{1}{2}</math> <span style="color: darkblue">(xcm+ycm)</span>•<span style="color: darkorange">4cm</span> = (xcm+ycm)•4cm•<math>\frac{1}{2}</math> = (xcm+ycm)•2cm | ||
| + | |||
| + | Um den Flächeninhalt des Drachenvierecks A<sub>DV</sub> zu erhalten, muss man den Flächeninhalt des Teildreiecks verdoppeln: '''A<sub>DV</sub>''' = 2•A<sub>D</sub> = 2•(xcm+ycm)•2cm ='''4cm•(xcm+ycm)''' | ||
| + | |||
| + | |||
| + | * A(8cm;2cm)= 4cm(8cm+2cm)= 4cm•10cm= 40cm<sup>2</sup> | ||
| + | * A(10cm;5cm)= 4cm(10cm+5cm)= 4cm•15cm= 60cm<sup>2</sup> | ||
| + | * A(12cm;9cm)= 4cm(12cm+9cm)= 4cm•21cm= 84cm<sup>2</sup> | ||
| + | * A(15cm;13cm)= 4cm(15cm+13cm)= 4cm•28cm= 112cm<sup>2</sup> | ||
| + | </popup> </div> | ||
Version vom 11. August 2010, 10:59 Uhr
Inhaltsverzeichnis |
Aufstellen und Interpretieren von Termen
Aufstellen von Termen
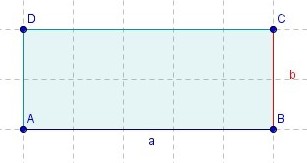
Übertrage die Zeichnung in dein Heft und überlege dir einen Term, mit dem du den Flächeninhalt ausrechnen kannst.
Setze nun für a=2cm und b=3cm ein
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Rezept
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
Interpretieren von Termen
|
|
Übungsaufgaben
a) Addiere 2 zum Quadrat von x
b) Addiere 6 zum vierfachen der Zahl n
c) Multipliziere die Summe aus b und der Zahl 7 mit 4
d) Multipliziere x mit seiner Gegenzahl
e) Multipliziere den Vorgänger der natürlichen Zahl n mit seinem Nachfolger
|
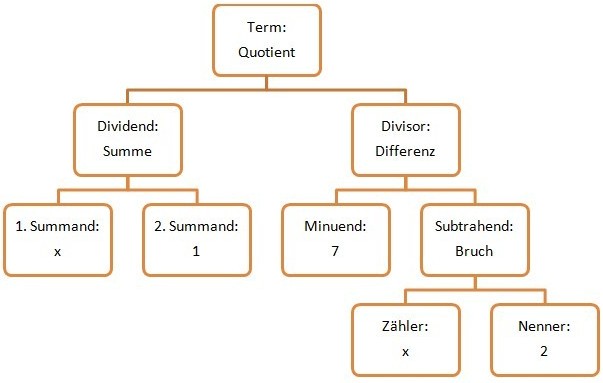
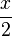 )
)
 ) = 5:(7-2) = 5:5 = 1
) = 5:(7-2) = 5:5 = 1