2003 I: Unterschied zwischen den Versionen

Version vom 5. April 2010, 20:37 Uhr

Leistungskurs Mathematik (Bayern): Abiturprüfung 2003 Infinitesimalrechnung I

Erarbeitet von Lukas Baumüller, Florian Wilk

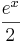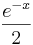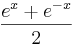g: x → ${e^x \over 2}$ , g^*:x → ${e^{-x} \over 2}$ und f₁: x → ${e^x+e^{-x} \over 2}$ .

Zeichnen Sie mit Hilfe der Funktionswerte g(-1) , g(1) und g(2) den Graphen von g im Bereich -2 $\le$ x $\le$ 2 in ein Koordinatensystem mit der Längeneinheit 2 cm.
Erläutern Sie, wie der Graph von g^* aus dem Graphen von g und schließlich der Graph von f₁ aus den Graphen von g und g^* entsteht. Zeichnen Sie die Graphen von g^* und f₁ in das vorhandene Koordinatensystem. 6 BE

folgt demnächst...

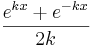Die Funktion f₁ gehört der Funktionenschar f_k: x → ${e^{kx}+e^{-kx} \over 2k}$ mit D = $\mathbb{R}$ und k $\in$ $\mathbb{R}$ ⁺ an.
Der Graph von f_k wird mit G_k bezeichnet.

b) Welches Symmetrieverhalten weist G_k auf?
Bestimmen Sie das Monotonieverhalten von f_k und geben Sie die Koordinaten des Extrempunktes an. 5 BE

folgt demnächst...

c) Nun wird die Integralfunktion F_k: x → $\int\limits_{0}^{x} f_k(t)dt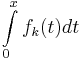$ mit dem Definitionsbereich $\mathbb{R}$ betrachtet.
Bestimmen Sie ohne Berechnung der integralfreien Darstellung von F_k das Symmetrie-, Monotonie- und Krümmungsverhalten des Graphen von F_k (kurze Begründung). 6 BE

folgt demnächst...

d) Ermitteln Sie eine integralfreie Darstellung von F₁(x) und zeigen Sie die Gültigkeit der Beziehung [f₁(x)]²=1+[F₁(x)]² für alle x $\in$ $\mathbb{R}$ .
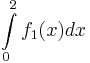Konstruieren Sie mittels dieser Beziehung den Wert J des Integrals $\int\limits_{0}^{2} f_1(x)dx$ als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig. 8 BE

folgt demnächst...

a) Ermitteln Sie die beiden Stellen x₁ und x₂ , an denen die Funktion f₁ den Wert m (m > 1) annimmt. 4 BE

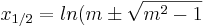[Ergebnis: $x_{1/2}=ln(m\pm\sqrt{m^2-1}$ ]

folgt demnächst...

b) Lässt man das im 1. Quadranten liegende, von G₁, der positiven y-Achse und der Geraden mit der Gleichung y = 10 begrenzte Flächenstück um die y-Achse rotieren, entsteht ein kelchförmiger Körper. Berechnen Sie dessen Durchmesser d am oberen Rand.
Geben Sie einen Ansatz für das Volumen V des Kelches an (Berechnung ist nicht verlangt). 5 BE

folgt demnächst...

Die Spannweite am Boden (Außenmaße)und die Höhe des 1965 in St. Louis, Missouri, errichteten Gateway Arch betragen jeweils 631 feet. Das Foto zeigt eine Schrägansicht des Bogens. In einem Koordinatensystem mit der Längeneinheit 1 foot kann die äußere Begrenzung des Bogens durch einen umgedrehten Graphen G_k angenähert werden. Erstellen Sie einen Ansatz zur Berechnung von k und zeigen Sie, dass der Wert k=2^-7 eine gute Näherungslösung ist. 6 BE

folgt demnächst...

Version vom 5. April 2010, 20:33 Uhr (Quelltext anzeigen) Wilk Florian (Diskussion \| Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 5. April 2010, 20:37 Uhr (Quelltext anzeigen) Wilk Florian (Diskussion \| Beiträge) Zum nächsten Versionsunterschied →
Zeile 38:		Zeile 38:


−	; Die Funktion f<sub>1</sub> gehört der Funktionenschar f<sub>k</sub>: x → <math>{e^{kx}+e^{-kx} \over 2k}</math> mit D = <math>\mathbb{R}</math> und k<math>\in</math><math>\mathbb{R}</math><sup>+</sup> an.	+	; ''Die Funktion f<sub>1</sub> gehört der Funktionenschar f<sub>k</sub>: x → <math>{e^{kx}+e^{-kx} \over 2k}</math> mit D = <math>\mathbb{R}</math> und k<math>\in</math><math>\mathbb{R}</math><sup>+</sup> an.''
−	; Der Graph von f<sub>k</sub> wird mit G<sub>k</sub> bezeichnet.	+	; ''Der Graph von f<sub>k</sub> wird mit G<sub>k</sub> bezeichnet.''