2004 II: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Isabell, Ann Christin, Johanna) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | |
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2006'''</big></center> | ||
| + | <center><big>'''Infinitesimalrechnung II'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=ff574c530ac05ed359667c29b75a15ff '''Download der Originalaufgaben: Abitur 2004 LK Mathematik Bayern'''] - [[]]</center> | ||
| + | |||
| + | |||
| + | <center>Erarbeitet von Johanna Buchner, Isabell Geist und Ann Christin Werner</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
| + | |||
| + | Gegeben ist die Funktion <math>f:\vec{x}\mapsto \ln\left(\frac{4}{x} -1\right)</math> mit dem maximalen Definitionsbereich D<sub>f</sub> = ]0;4[. Der Graph von f wird mit G<sub>f</sub> bezeichnet. | ||
| + | |||
| + | |||
| + | |||
| + | a) Berechnen Sie die Nullstelle von f und untersuchen Sie das Verhalten von f an den Rändern von D<sub>f</sub>. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | b) Untersuchen Sie das Monotonieverhalten von f. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | c) Zeigen Sie, dass G<sub>f</sub> punktsymmetrisch zu Z(2|0) ist. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | d) Berechnen Sie <math>f (0,5)</math>. Zeichnen Sie G<sub>f</sub> unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte). | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | f besitzt eine Umkehrfunktion, die mit g bezeichnet wird. | ||
| + | |||
| + | |||
| + | e) Zeigen Sie, dass gilt: <math>g(x) = 4 - \frac{4e^{x} }{1+e^{x} }</math>. Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:]] | ||
| + | |||
| + | |||
| + | <ggb_applet width="612" height="450" version="3.2" ggbBase64="UEsDBBQACAAIAEiseTwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVbNbuM2ED53n4LQKWkRW9SPLQNWFu0WBQKk3YPbPfTQgpZGNmuKNEgqkfdl+jB9sQ5JyXa8SbYtFj0YImeGw5lvvhl6+bZvBXkAbbiSZUQncURAVqrmclNGnW1uiujt7ZvlBtQG1pqRRumW2TJKJ0nk5B2/ffPV0mzVI2HCm3zg8FhGDRMGImL2GlhttgD2iZx1PRec6cP79R9QWXNSBCd3ct/hLVZ3KKva+p6bcTv1F+4Ft9/zB16DJkJVZTTLMXRcfQBtecVEGWVxkCSonD3RoSR1yq3S/KOS1lmffDcoIcTwj4CAFE62nPo8l9BVgtecSZeLDwONCHnktd3iJTRBl8A3Www1y4rgrVJK16uDsdCS/lfQCnV5MomzOE+KdJZl8wUeOwRNms8nyWy+yOhslidphmEbjBcDKRaTBK3zOKGLIs3iDM+8qPIXw8MKrMU6GsJ6MCOYG83r8/Wd+U6J+oj/XnFp37G97bSnQDqIVvbg7kLQtEvwW7kRMMgw/GoL1W6t+lUALQ2ufz7s/REfznrzTgmlicYDeY4Gw3cdvt7GxXm0ir1N7C0GH87pUU8dbpvhuw5fbyW4DKENedMx6Xi8hRsS9sQRd0RDsDUgESLSSW7vxw0SZjckSoP9T127xoY5p8zRJf1CLpfTC64td6AliMAoiWXtVGfIg2NuqJyPo4aKt7gNigEP5mr1CwYQpDVsNIxxh24LaHltfM7aC/FyOgbhYjAYa2VxbGA+1uXiutpiS5XRymr215/YCi125w9YL0wjIjWzzsr1kYAWsMmsJ4js0IxXR7R2kYsAr+2Gy5PJwA8/ZpSfGBcIn0qB6hcohLNlv2W4mtCBKOyA8Z2n7b39qOrh4sHOCD9mWi7dYXTUsr6Mcrdia6NEZ2FVIabyXlXM+kEaghsGA439KTxDk5lbHcponrlFw3s49d7z4+hEZ7tF4kgwxvecPe8uJrHuvhg4aPYhRxy+AIGToy3ZY86+r4+kQaaFany2LvBpXea0SAr3y/JFnD1XpSG1/6NMHswgOevM8aF5qniSdY+PlHEP4Bhmg49gjyg2V/01KcmOTMkVPo3kGwK/Xd1c7a7J16S/vo7I9BPQmk76pohOvl4sYn5RxC9F7/hV3N43jQHr2Vh4Kt6k6bOwpq/w7zL0Cl8MB2AYSL/vELhLmCvVtkzWRLIWz91Ji3OICY8Od689YbFHnlEMifqOYclZOqqzoxULvgePnyUuuyRuPJktUpohe+OsSBNKs/9WAJqnvgQ5/ZfcPdWgCOPghr7G7H80Ap6UQMjkEv/p+cz2/2mG/3S3fwNQSwcIY0lV/doDAAAFCgAAUEsBAhQAFAAIAAgASKx5PGNJVf3aAwAABQoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAAUBAAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | |||
| + | Zwei Gänge von 2,0 m und 4,0 m Breite treffen rechtwinklig aufeinander. | ||
| + | |||
| + | Es soll die größtmögliche Länge L eines Balkens ermittelt werden, den man in horizontaler Lage aus einem Gang in den anderen tragen kann. Die Dicke des Balkens wird als vernachlässigbar klein angesehen. | ||
| + | |||
| + | |||
| + | Dazu betrachte man die gezeichnete Figur. <math>l(\alpha )</math> ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° < <math>\alpha</math> < 90° die Funktion <math>l</math>. | ||
| + | |||
| + | |||
| + | a) Geben Sie an, welche Bedeutung die Maßzahl der gesuchten Länge für die Funktion <math>l</math> hat. Zeigen Sie: <math>l(\alpha ) = \frac{2}{\sin(\alpha ) } + \frac{4}{\cos(\alpha )} </math>. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | b) Berechnen Sie L auf dm genau. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Version vom 28. März 2010, 15:20 Uhr
|
|
Gegeben ist die Funktion
a) Berechnen Sie die Nullstelle von f und untersuchen Sie das Verhalten von f an den Rändern von Df.
[[Bild:]]
[[Bild:]]
[[Bild:]]
|
Zwei Gänge von 2,0 m und 4,0 m Breite treffen rechtwinklig aufeinander. Es soll die größtmögliche Länge L eines Balkens ermittelt werden, den man in horizontaler Lage aus einem Gang in den anderen tragen kann. Die Dicke des Balkens wird als vernachlässigbar klein angesehen.
[[Bild:]]
[[Bild:]]
|
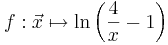 mit dem maximalen Definitionsbereich Df = ]0;4[. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = ]0;4[. Der Graph von f wird mit Gf bezeichnet.
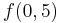 . Zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte).
. Zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte).
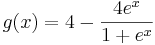 . Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein.
. Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein.
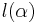 ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° <
ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° <  < 90° die Funktion
< 90° die Funktion 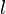 .
.
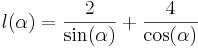 .
.

