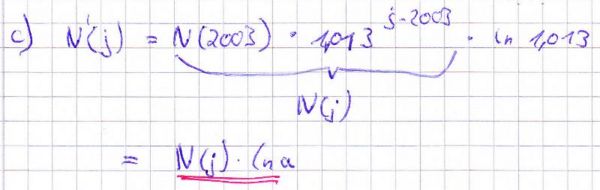2005 I: Unterschied zwischen den Versionen
(Lösung zum Ausdrucken hochgeladen) |
|||
| Zeile 32: | Zeile 32: | ||
'''Aufgabe 1''' | '''Aufgabe 1''' | ||
| − | Gegeben ist die Schar der in | + | Gegeben ist die Schar der in IR definierten Funktionen <math>f_k:x\rightarrow (x^2+1-k)e^{-x}</math> mit <math> k \in \mathbb{R} </math> |
Der Graph von f<sub>k</sub> wird mit G<sub>k</sub>bezeichnet. | Der Graph von f<sub>k</sub> wird mit G<sub>k</sub>bezeichnet. | ||
| Zeile 50: | Zeile 50: | ||
<div align="right"><i>'''4 BE'''</i></div> | <div align="right"><i>'''4 BE'''</i></div> | ||
| − | <b>c)</b> Für welche Werte von k besitzt G<sub>k</sub> mindestens eine waagrechte Tangente? Zeigen Sie, dass | + | <b>c)</b> Für welche Werte von k besitzt G<sub>k</sub> mindestens eine waagrechte Tangente? Zeigen Sie, dass die Punkte von G<sub>k</sub> mit waagrechter Tangente auf dem Graphen W der Funktion <Math> w: x \rightarrow 2xe^{-x}</math> mit <math> x \in \mathbb{R} </math> liegen. |
<popup name ="Lösung"> | <popup name ="Lösung"> | ||
| Zeile 58: | Zeile 58: | ||
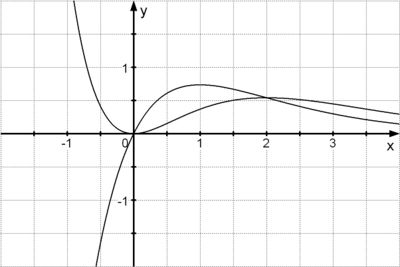
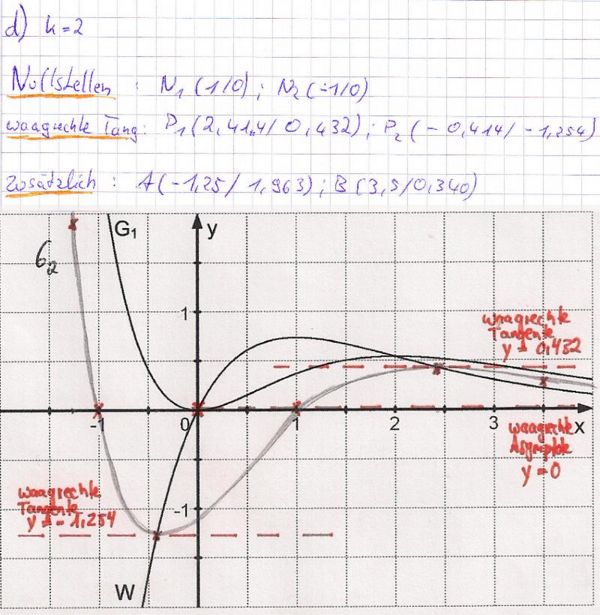
| − | <b>d)</b> Die unten stehende Abbildung zeigt die Graphen G<sub>1</sub> und W. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den | + | <b>d)</b> Die unten stehende Abbildung zeigt die Graphen G<sub>1</sub> und W. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen G<sub>2</sub> in die Abbildung ein. |
[[Bild: 2005_1_1d_Zusatzbild zu d.jpg | 400px | center]] | [[Bild: 2005_1_1d_Zusatzbild zu d.jpg | 400px | center]] | ||
| Zeile 67: | Zeile 67: | ||
<div align="Right"><i>'''5 BE'''</i></div> | <div align="Right"><i>'''5 BE'''</i></div> | ||
| − | <b>e)</b> Bestätigen Sie, dass für <math>k \in \mathbb{R} </math> gilt: <math>f_k(x) = w(x) -f_{k}^{'}(x)</math> | + | <b>e)</b> Bestätigen Sie, dass für <math>k \in \mathbb{R} </math> gilt: <math>f_k(x) = w(x) -f_{k}^{'}(x)</math>. |
| − | Der | + | Der Graph G<sub>1</sub> begrenzt im ersten Quadranten mit der x-Achse ein sich ins Unendliche erstreckendes Flächenstück mit endlichem Inhalt. Berechnen Sie diesen Flächeninhalt mit Hilfe der obigen Beziehung. |
<popup name= "Lösung"> | <popup name= "Lösung"> | ||
Version vom 16. März 2010, 16:29 Uhr
|
|
|
Aufgabe 1 Gegeben ist die Schar der in IR definierten Funktionen Der Graph von fk wird mit Gkbezeichnet. a) Untersuchen Sie fk auf Nullstellen in Abhängigkeit von k. Bestimmen Sie das Verhalten von fk für 4 BE
b) Zeigen Sie, dass sich je zwei verschiedene Graphen Gk nicht schneiden, einander aber beliebig nahe kommen. 4 BE
c) Für welche Werte von k besitzt Gk mindestens eine waagrechte Tangente? Zeigen Sie, dass die Punkte von Gk mit waagrechter Tangente auf dem Graphen W der Funktion 7 BE
5 BE
e) Bestätigen Sie, dass für 7 BE
Aufgabe 2 In einer Fachzeitschrift war zu lesen: "Am oder um den 12. Oktober 1999 hat die Weltbevölkerung die Grenze von sechs Milliarden Menschen überschritten. Zu Beginnn des Jahres 2003 lebten bereits 6,274 Milliarden Erdenbürger. Im Jahr 2003 wurden im weltweiten Durchschnitt auf tausend Menschen, die zu Jahresbeginnn lebten, 22 Geburten und 9 Todesfälle gezählt." a) Wieviele Kinder wurden 2003 im Durchschnitt näherungsweise pro Minute geboren? Wieviele Milliarden Menschen lebten zu Beginn des Jahres 2004? 4 BE
b) Sollte sich die Bevölkerungsentwicklung von 2003 in Zukunft nicht ändern, so ließe sich die Anzahl 6 BE
c) Bilden Sie die ABleitung der Funktion 3 BE
(40 BE)
|
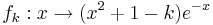 mit
mit 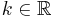
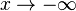 und
und 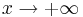 .
.


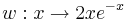 mit
mit  liegen.
liegen.

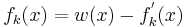 .
Der Graph G1 begrenzt im ersten Quadranten mit der x-Achse ein sich ins Unendliche erstreckendes Flächenstück mit endlichem Inhalt. Berechnen Sie diesen Flächeninhalt mit Hilfe der obigen Beziehung.
.
Der Graph G1 begrenzt im ersten Quadranten mit der x-Achse ein sich ins Unendliche erstreckendes Flächenstück mit endlichem Inhalt. Berechnen Sie diesen Flächeninhalt mit Hilfe der obigen Beziehung.


 der Erdenbürger zu Beginn des Jahres j nach der Formel
der Erdenbürger zu Beginn des Jahres j nach der Formel 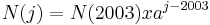 berechnen.
Bestimmen Sie a und das Kalenderjahr, in dem die Zahl von neun Milliarden Menschen überschritten würde.
berechnen.
Bestimmen Sie a und das Kalenderjahr, in dem die Zahl von neun Milliarden Menschen überschritten würde.

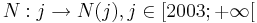 .
Welcher Zusammenhang besteht zwischen
.
Welcher Zusammenhang besteht zwischen 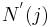 ?
?