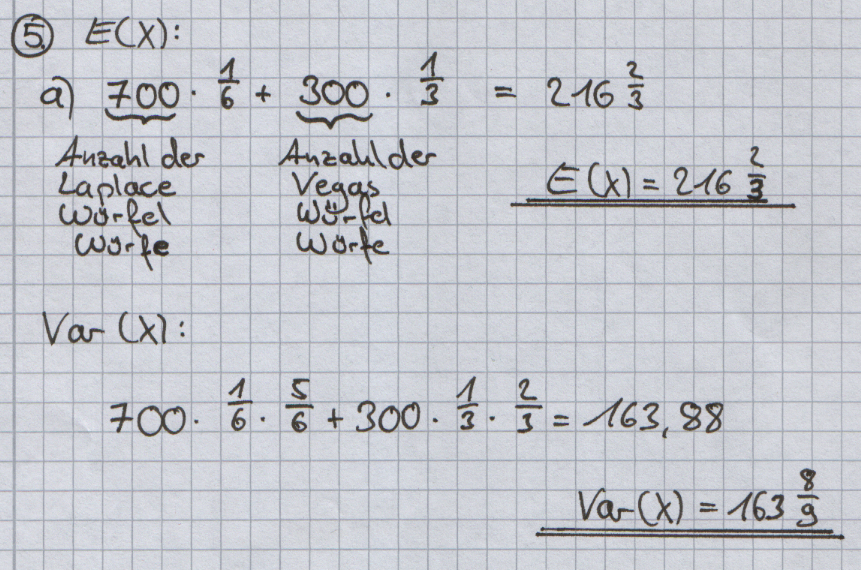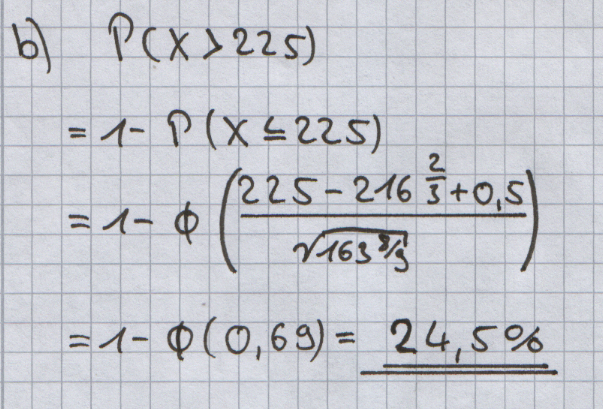2003 IV: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung | + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2003'''</big></center> |
<center><big>'''Stochastik IV'''</big></center> | <center><big>'''Stochastik IV'''</big></center> | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID= | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:LKM Abi 2003 IV lös.doc|Lösung gesamt]]</center> |
| Zeile 25: | Zeile 25: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | Zeigen Sie, dass der Erwartungswert der Zufallsgröße „Augenzahl beim einmaligen Werfen eines Vegas-Würfels“ 4 ist. | + | Im Januar 2002 war in einer Zeitung zu lesen, dass die neuen Euro- |
| + | Münzen keine Laplace-Münzen seien. Bei einem Experiment mit einer | ||
| + | 2-Euro-Münze, die man 1000-mal auf dem Tisch kreiseln ließ, sei | ||
| + | 600-mal Zahl oben liegen geblieben. | ||
| + | |||
| + | '''a)''' Zeigen Sie, dass der Erwartungswert der Zufallsgröße „Augenzahl beim einmaligen Werfen eines Vegas-Würfels“ 4 ist. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:1.jpg]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | '''b)''' bla | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:1.jpg]] | ||
| + | }} | ||
| + | |||
| + | '''c)''' bla | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:1.jpg]] | ||
| + | }} | ||
| + | |||
| + | '''d)''' bla | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
Version vom 11. April 2010, 14:44 Uhr
|
|
|
Im Januar 2002 war in einer Zeitung zu lesen, dass die neuen Euro- Münzen keine Laplace-Münzen seien. Bei einem Experiment mit einer 2-Euro-Münze, die man 1000-mal auf dem Tisch kreiseln ließ, sei 600-mal Zahl oben liegen geblieben. a) Zeigen Sie, dass der Erwartungswert der Zufallsgröße „Augenzahl beim einmaligen Werfen eines Vegas-Würfels“ 4 ist.
c) bla d) bla |
Auf dem Tisch liegen ungeordnet drei Laplace-Würfel und ein Vegas-Würfel. Ein Spieler nimmt davon zufällig drei Würfel und wirft sie gleich¬zeitig. Mit welcher Wahrscheinlichkeit erzielt er drei gleiche Augenzahlen, wenn er drei Laplace-Würfel genommen hat? Mit welcher Wahrschein-lichkeit erzielt er drei gleiche Augenzahlen, wenn er zwei Laplace-Würfel und den Vegas-Würfel genommen hat? Welche Folgerung können Sie aus Ihren Ergebnissen bezüglich der stochastischen Abhängigkeit der Ereignisse „Er erzielt drei gleiche Augenzahlen“ und „Er nimmt drei Laplace-Würfel“ ziehen? |
Um bei einem Würfel festzustellen, ob es sich um einen Laplace- oder Vegas-Würfel handelt, wird er 100 mal geworfen. Ein Vegas-Würfel soll mit einer Wahrscheinlichkeit von mindestens 99 % als solcher eingestuft werden.
Bestimmen Sie hierzu die Entscheidungsregel anhand der Anzahl der geworfenen Sechser so, dass möglichst auch ein Laplace-Würfel richtig eingestuft wird. [Ergebnis: Entscheidung für Vegas-Würfel ab 23 geworfenen Sechsern]
Mit welcher Wahrscheinlichkeit wird bei dieser Entscheidungsregel ein Laplace-Würfel falsch eingestuft? |
|
Eine Packung des Spiels enthält – ungeordnet und äußerlich nicht unter-scheidbar – 7 Laplace- und 3 Vegas-Würfel.
Aus dieser Packung wird ein Würfel entnommen und 100-mal geworfen. Mit welcher Wahrschein¬lichkeit handelt es sich um einen Vegas-Würfel, wenn dabei 25-mal eine „6“ geworfen wird? |
Die 10 Würfel werden nun einzeln nacheinander aus der Packung ent-nommen und je 100-mal geworfen.
Die Zufallsgröße X bezeichne die Anzahl der geworfenen Sechser unter den insgesamt 1000 durchzuführenden Würfen. Berechnen Sie Erwartungs¬wert und Varianz von X.
[Ergebnis:
Die Zufallsgröße X ist näherungsweise normalverteilt. Berechnen Sie mit Hilfe der Normalverteilung, mit welcher Wahrscheinlichkeit bei den 1000 Würfen mehr als 225-mal eine „6“ geworfen wird. |
Bei einem Spiel werden jeweils 5 Würfel geworfen. Aus den Augen-zahlen – aufgefasst als Ziffern – werden möglichst große fünfstellige natürliche Zahlen gebildet, z. B. 43321, nicht jedoch 34312.
Mit welcher Wahrscheinlichkeit erhält man eine Zahl größer als 50000, wenn es sich um 5 Laplace-Würfel handelt?
Wie viele verschiedene natürliche Zahlen können nach dieser Spiel-regel gebildet werden? Wählen Sie aus den folgenden kombina-torischen „Modellen“ zunächst das für dieses Problem passende aus und bestimmen Sie dann mit dessen Hilfe die gesuchte Anzahl. A) Anzahl der fünfstelligen Zahlen aus den Ziffern 1 bis 6 dividiert durch die Zahl der Permutationen von 5 Elementen B) Zahl der möglichen Verteilungen von 5 Kugeln auf 6 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt C) Zahl der möglichen Verteilungen von 6 Kugeln auf 5 Urnen, wobei es nur auf die jeweilige Anzahl der Kugeln in den Urnen ankommt |



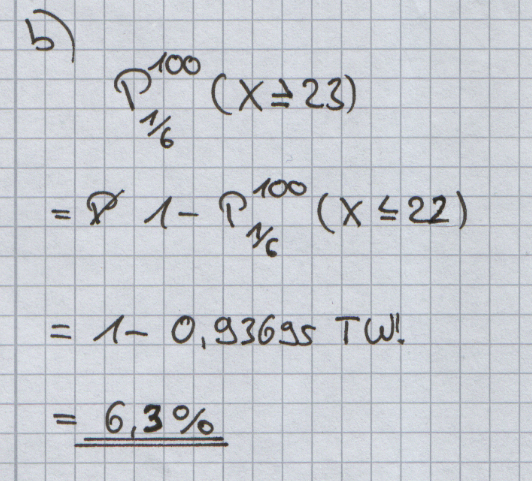

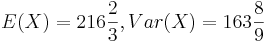 ]
]