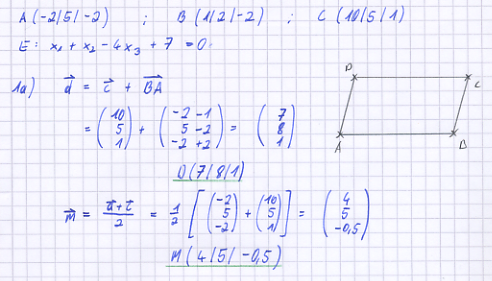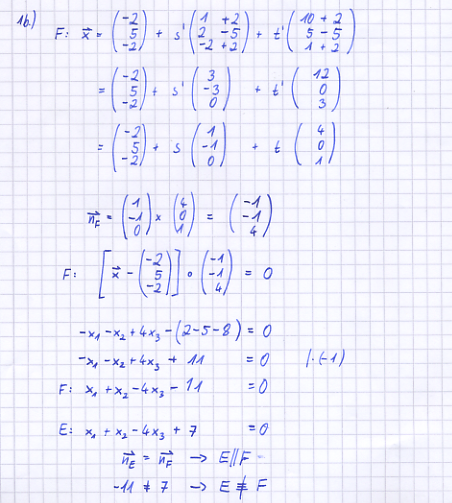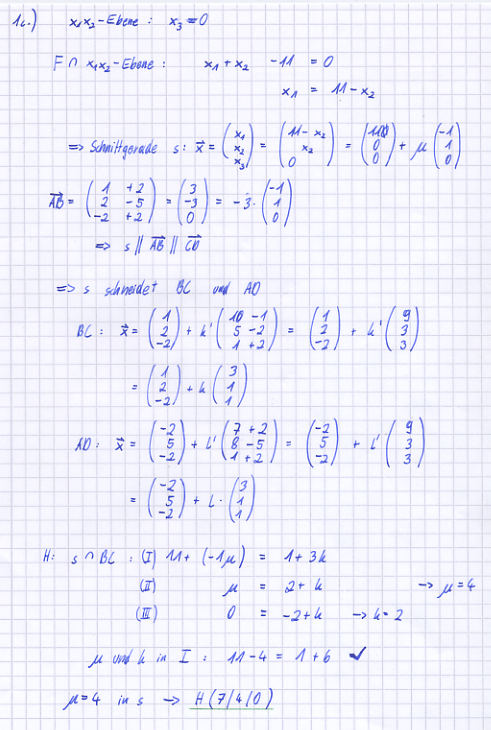2004 V: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 25: | Zeile 25: | ||
| − | In einem kartesischen Koordinatensystem des | + | In einem kartesischen Koordinatensystem des R<sup>3</sup> sind die Punkte A(-2|5|-2), B(1|2|-2), C(10|5|1) sowie die Ebene E: x<sub>1</sub> + x<sub>2</sub> - 4 x<sub>3</sub> + 7 = 0 gegeben. |
| Zeile 57: | Zeile 57: | ||
| − | c) Die Parallelogrammfläche schneidet die | + | c) Die Parallelogrammfläche schneidet die x<sub>1</sub>x<sub>2</sub>-Ebene in der Strecke [GH]. Berechnen Sie die Koordinaten der Punkte der Punkte G und H und tragen Sie die Strecke [GH] in die angelegte Zeichnung ein. |
[Zur Kontrolle: (4|7|0) und (7|4|0)] | [Zur Kontrolle: (4|7|0) und (7|4|0)] | ||
| Zeile 66: | Zeile 66: | ||
| − | d) In welchem Verhältnis wird die Fläche des Parallelogramms durch die | + | d) In welchem Verhältnis wird die Fläche des Parallelogramms durch die x<sub>1</sub>x<sub>2</sub>-Ebene geteilt? Begründen Sie Ihre Antwort. |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
Version vom 10. März 2010, 14:05 Uhr
|
|
|
|
a) Bestimmen Sie die Koordinaten des Punktes D so, dass das Viereck ABCD ein Parallelogramm ist, und berechnen Sie die Koordinaten des Diagonalenschnittpunkts M. Legen Sie ein Koordinatensystem an (Querformat, Ursprung in Seitenmitte) und tragen Sie das Parallelogramm ABCD sowie den Punkt M ein. [Zur Kontrolle: M(4|5|-0,5)]
[Zur Kontrolle: (4|7|0) und (7|4|0)]
|
|