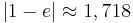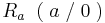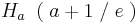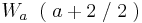Lösungsübersicht: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Teilaufgabe c)) |
(→Teilaufgabe d)) |
||
| Zeile 38: | Zeile 38: | ||
=== Teilaufgabe d) === | === Teilaufgabe d) === | ||
| − | 1. | + | 1. <math>R_a \;\;(\; a\; /\; 0\; )\;</math><br /> |
| − | + | <math>H_a \;\;(\; a + 1 \;/\; e\; )\;</math><br /> | |
| − | + | <math>W_a \;\;(\; a + 2 \;/\; 2 \;)\;</math><br /> | |
Da sich die y-Werte dieser Punkte nicht verändern, haben diese immer denselben Abstand <br /> zueinander. Deshalb sind alle Dreiecke, die durch diese Punkte festgelegt sind, kongruent. | Da sich die y-Werte dieser Punkte nicht verändern, haben diese immer denselben Abstand <br /> zueinander. Deshalb sind alle Dreiecke, die durch diese Punkte festgelegt sind, kongruent. | ||
Version vom 20. Januar 2010, 19:22 Uhr
Inhaltsverzeichnis |
Funktion
Stammfunktion: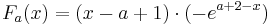
Funktion: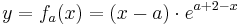
1. Ableitung: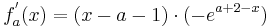
2. Ableitung: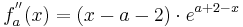
3. Ableitung: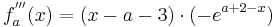
Teilaufgabe a)
Nullstelle: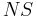
Schnittpunkt mit der y-Achse:
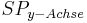
Extrempunkt:
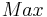
Wendepunkt:
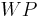
Funktionsgleichung aller Extrempunkte:
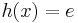
Teilaufgabe b)
1. Fürist der GFa streng monoton fallend.
Fürist der GFa streng monoton steigend.
Fürbesitzt GFa eine Tiefpunkt.
2. Stammfunktion: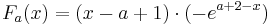
3. Flächeninhalt zwischen der x-Achse und dem Graphen der Funktion f2: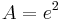
Teilaufgabe c)
1.2.
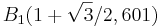
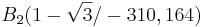
Teilaufgabe d)
1.
Da sich die y-Werte dieser Punkte nicht verändern, haben diese immer denselben Abstand
zueinander. Deshalb sind alle Dreiecke, die durch diese Punkte festgelegt sind, kongruent. 2.