Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎2.Verschiebung nach rechts/links)
Zeile 1: Zeile 1:
 +
{|
 +
! width="910" |
 +
|-
 +
| valign="top" |
 
= <span style="color: blue">Verschieben von Funktionsgraphen</span> =
 
= <span style="color: blue">Verschieben von Funktionsgraphen</span> =
 
==<span style="color: blue">1.Verschiebung nach oben/unten</span> ==
 
==<span style="color: blue">1.Verschiebung nach oben/unten</span> ==
Zeile 10: Zeile 14:
 
'''<span style="color: blue">Erklärung:</span>''' <br />
 
'''<span style="color: blue">Erklärung:</span>''' <br />
 
Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der rote Graph g liegt jeweils so viele Eineiten über bzw unter dem Graphen f, wie der Regler anzeigt. <br />
 
Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der rote Graph g liegt jeweils so viele Eineiten über bzw unter dem Graphen f, wie der Regler anzeigt. <br />
−
Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als <br />
+
Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als  
 
der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings <span style="color: blue">um a Einheiten nach oben (in positiver y-Richtung) bzw. <br />
 
der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings <span style="color: blue">um a Einheiten nach oben (in positiver y-Richtung) bzw. <br />
 
nach unten (in negativer y-Richtung) verschoben</span>.  <br />  
 
nach unten (in negativer y-Richtung) verschoben</span>.  <br />  
Zeile 75: Zeile 79:
 
[[Bild:Aufgabe 2 Verschiebungen 1.png|400px]] <br /> <br />
 
[[Bild:Aufgabe 2 Verschiebungen 1.png|400px]] <br /> <br />
  
−
a) [[Bild:Aufgabe 2 Verschiebungen 2.png|400px]] b) [[Bild:Aufgabe 2 Verschiebungen 3.png|400px]] c) [[Bild:Aufgabe 2 Verschiebungen 4.png|400px]] <br /> <br />
+
a) [[Bild:Aufgabe 2 Verschiebungen 2.png|400px]] b) [[Bild:Aufgabe 2 Verschiebungen 3.png|400px]] <br />
 +
c) [[Bild:Aufgabe 2 Verschiebungen 4.png|400px]] <br /> <br />
  
  
Zeile 131: Zeile 136:
  
 
</quiz>
 
</quiz>
−
 
+
|}
  
 
[[Facharbeit Florian Wilk/Strecken und Spiegeln von Funktionsgraphen|Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen]]
 
[[Facharbeit Florian Wilk/Strecken und Spiegeln von Funktionsgraphen|Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen]]

Version vom 19. Januar 2010, 16:01 Uhr

Inhaltsverzeichnis

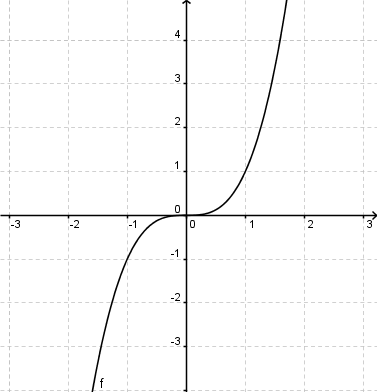
Verschieben von Funktionsgraphen

1.Verschiebung nach oben/unten

Problemstellung:
Im untenstehenden Applett siehst du den Funktionsgraphen f der Funktion f(x)=x3. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben
des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt.




Erklärung:
Der Graph f gehört zu dem Funktionsterm f(x)=x3. Der rote Graph g liegt jeweils so viele Eineiten über bzw unter dem Graphen f, wie der Regler anzeigt.
Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings um a Einheiten nach oben (in positiver y-Richtung) bzw.
nach unten (in negativer y-Richtung) verschoben.

Für den Funktionsterm g(x) gilt somit: g(x)=f(x)+a.

Beispiel: f(x)=x3


f(2)=8

Verschiebung um 3 Einheiten nach oben \rightarrow g(x)=f(x)+3

g(2)=f(2)+3
g(2)=8+3
g(2)=11



Merke:

Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x)+a entsteht der Graph g durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung.

Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten).




2.Verschiebung nach rechts/links

Problemstellung:
Im untenstehenden Applett siehst du den Graphen f mit x→x3+2x2 und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst.
Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauzufinden.




Erklärung:
Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben
nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings um b Einheiten nach rechts bzw. links verschoben. Somit entspricht
der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.
Das bedeutet für den funktionellen Zusamenhang: g(x)=f(x-3).

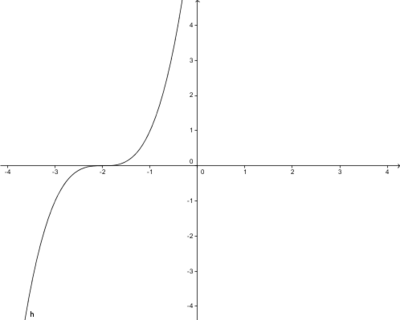
Beispiel: f(x)=x3+2x2
x=1 \rightarrow f(1)=3

Verschiebung um 3 Einheiten nach rechts:

g(x)=f(x-3)
g(x)=(x-3)3+2(x-3)2
g(4)=(4-3)3+2(4-3)2
g(4)=1+2=3=f(1)


Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von g(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.


Merke:
Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).

3.Beispielaufagben

Aufgabe 1:
Gegeben ist die Funktion f(x)=x3+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.



Aufgabe 2:
Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x3 hervorgegangen sind.

Ausgangsfunktion:
Aufgabe 2 Verschiebungen 1.png

a) Aufgabe 2 Verschiebungen 2.png b) Aufgabe 2 Verschiebungen 3.png
c) Aufgabe 2 Verschiebungen 4.png




Aufgabe 3:
Kreuze an, was stimmt. Es können mehrere Antwortmöglichkeiten richtig sein.

1. In welche Richtung ist der Graph f(x)=3x4+3x2-2x+4 ist gegenüber dem Graphen g(x)=3x4+3x2-2x verschoben?

nach oben
nach unten
nach links
in positiver y-Richtung
nach rechts

2. Um wie viele Einheiten ist der Graph g(x)=2x3+x2+4 gegenüber dem Graphen f(x)=2x3+x2-2 nach oben verschoben?

4
gar nicht
6
2

3. Wie lautet der Funktionsterm der Funktion, die ausgehend von der Funktion f(x)=x3+2x um 1 Einheit nach unten und 2 Einheiten nach links verschoben ist?

g(x)=x3+2x-1
g(x)=x3+6x2+14x+11
g(x)=x3+2x-3
g(x)=(x+2)3+2(x+2)-1
g(x)=(x-2)3+2(x-2)-1

4. In welche Richtung ist die Funktion g(x)=(x+3)2+2 gegenüber der Funktion f(x)=x2+2 verschoben?

nach links
nach rechts
in positiver y-Richtung
in positiver x-Richtung
in negativer x-Richtung
in negativer y-Richtung
nach oben
nach unten

Punkte: 0 / 0

Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen


Zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=Facharbeit_Florian_Wilk/Verschieben_von_Funktionsgraphen&oldid=27272“