Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen
(→2.Verschiebung nach rechts/links) |
(→1.Verschiebung nach oben/unten) |
||
| Zeile 2: | Zeile 2: | ||
==<span style="color: blue">1.Verschiebung nach oben/unten</span> == | ==<span style="color: blue">1.Verschiebung nach oben/unten</span> == | ||
| − | '''<span style="color: blue">Problemstellung:</span>''' | + | '''<span style="color: blue">Problemstellung:</span>''' <br /> |
| − | <ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAAORMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vffb9s2EH5e/wpCTy2GxJI8Fw1gpUg6FAiQNQPcdUAfBlDSWeJMkRpJOXL++h2PkuMfXeCs3QbsieLxdLr77uNHav62byRbg7FCqyxKzuOIgSp0KVSVRZ1bnr2J3l6+mFegK8gNZ0ttGu6yaHqeRt7eicsX381tre8Zl+TyScB9FjnTQcRsa4CXtgZwwbzk0qKdd72QgpvNXf47FM4+LoQYN6rt3BikaMpbYcfphL7XSuF+FGtRgmFSF1n0eoaZ49MnME4UXGbRD3GwpFmUHiyiaepXa23Eg1bOuz8GX6KFMSseAAFJvW0+oTrn0BVSlIIrXwzlgU6M3YvS1ZjC9DWGBFHVmOssiUO0QmtTLjbWQcP6z2A0ppPMPM6bMJuGmcW88IOzmJZ2ZxQG1gtwDrtiGe/BjthURpS7zzf2WstyC2erhXLveOs6Qw2dDqaF2/jw+CXj071SlYTBliLgNRSrXPeLAME0hP64aekVSiev3mmpDTMe3Bk6DGMeRvLxeW69YvKJyWOI4YNu15OLlDxozMNIXlKokNpQdzIWPQLMe2GZN3gQkYcjHJLngH2NWKeEux0n2P/VUGkS/D90TY7832XANmTyjULOJwfUma/AKJCBIAr72unOsrUnYmgd5VFCIRqchoUBEO6b9QsmEKwlVAbGvMPuCXDR6h4JD8zzyZiEz8FiroVDFcB6nK8FN4stagE5KLZG8/tOrfy6rQxva1B+FzvcQVn0HnuIlbFfhVxFrOQO3/biAD1uf+uVJSDHsDiUl77F8WX/imWs/+3l9Dx+RdmAhAZw5zni2bJTlM0W9GW0zwZXI+wKwxNl3S45SY00KctB5x5bjMt/wU3UoLbm+DRuPck3qDK7cFK0n3S5DzJX2CxCEDd76wN4OrQA5SCsY5KsxZC0H3d6fUJlyKKA0RFaqmvAiGJbJyewMLluSDE5/8bYJCdiM/hZSVLdCDxkzkjvGt6jvvknnlstOweLAomsbnVBII7ZDeKaxCSM+M6bC1JI1NvUPyxFD4+C92VFP4k1X9O+vc4csD6LqoH01R7p2feMR+wE5lf/HPNH7X4u9++WSwvOd+MsvaBmPLkznsntQjcNVyVTvMHln/2BRRAIfytgPPZiEErp3Gi5CkGGV49ApVNvC8ZVdATWwJ8n0UrSgBaNw0n3H6kFCbr1DUiG3UDjw85ODwe9v6DQZ6fPR7k6Qvn6OShf/w9RTr8O5QVU3n6A8xXWlwzg7sFdPg23HaKNeJb/zhH59xqSHEJ6NmIaH2J6UgXwhwo+Nly9RIP/BIVwWxClb+eNcniNARLU4/vVCqD119o79dFwZf2/TfDZubdtOznZvSTRP8HwT3T5J1BLBwgqgdzw+gMAAEUNAABQSwECFAAUAAgACAADkTI8KoHc8PoDAABFDQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAADQEAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" | + | Im untenstehenden Applett siehst du den Funktionsgraphen f der Funktion f(x)=x<sup>3</sup>. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt. <br /> <br /> |
| − | + | :<ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAAORMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vffb9s2EH5e/wpCTy2GxJI8Fw1gpUg6FAiQNQPcdUAfBlDSWeJMkRpJOXL++h2PkuMfXeCs3QbsieLxdLr77uNHav62byRbg7FCqyxKzuOIgSp0KVSVRZ1bnr2J3l6+mFegK8gNZ0ttGu6yaHqeRt7eicsX381tre8Zl+TyScB9FjnTQcRsa4CXtgZwwbzk0qKdd72QgpvNXf47FM4+LoQYN6rt3BikaMpbYcfphL7XSuF+FGtRgmFSF1n0eoaZ49MnME4UXGbRD3GwpFmUHiyiaepXa23Eg1bOuz8GX6KFMSseAAFJvW0+oTrn0BVSlIIrXwzlgU6M3YvS1ZjC9DWGBFHVmOssiUO0QmtTLjbWQcP6z2A0ppPMPM6bMJuGmcW88IOzmJZ2ZxQG1gtwDrtiGe/BjthURpS7zzf2WstyC2erhXLveOs6Qw2dDqaF2/jw+CXj071SlYTBliLgNRSrXPeLAME0hP64aekVSiev3mmpDTMe3Bk6DGMeRvLxeW69YvKJyWOI4YNu15OLlDxozMNIXlKokNpQdzIWPQLMe2GZN3gQkYcjHJLngH2NWKeEux0n2P/VUGkS/D90TY7832XANmTyjULOJwfUma/AKJCBIAr72unOsrUnYmgd5VFCIRqchoUBEO6b9QsmEKwlVAbGvMPuCXDR6h4JD8zzyZiEz8FiroVDFcB6nK8FN4stagE5KLZG8/tOrfy6rQxva1B+FzvcQVn0HnuIlbFfhVxFrOQO3/biAD1uf+uVJSDHsDiUl77F8WX/imWs/+3l9Dx+RdmAhAZw5zni2bJTlM0W9GW0zwZXI+wKwxNl3S45SY00KctB5x5bjMt/wU3UoLbm+DRuPck3qDK7cFK0n3S5DzJX2CxCEDd76wN4OrQA5SCsY5KsxZC0H3d6fUJlyKKA0RFaqmvAiGJbJyewMLluSDE5/8bYJCdiM/hZSVLdCDxkzkjvGt6jvvknnlstOweLAomsbnVBII7ZDeKaxCSM+M6bC1JI1NvUPyxFD4+C92VFP4k1X9O+vc4csD6LqoH01R7p2feMR+wE5lf/HPNH7X4u9++WSwvOd+MsvaBmPLkznsntQjcNVyVTvMHln/2BRRAIfytgPPZiEErp3Gi5CkGGV49ApVNvC8ZVdATWwJ8n0UrSgBaNw0n3H6kFCbr1DUiG3UDjw85ODwe9v6DQZ6fPR7k6Qvn6OShf/w9RTr8O5QVU3n6A8xXWlwzg7sFdPg23HaKNeJb/zhH59xqSHEJ6NmIaH2J6UgXwhwo+Nly9RIP/BIVwWxClb+eNcniNARLU4/vVCqD119o79dFwZf2/TfDZubdtOznZvSTRP8HwT3T5J1BLBwgqgdzw+gMAAEUNAABQSwECFAAUAAgACAADkTI8KoHc8PoDAABFDQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAADQEAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> | |
| + | |||
| − | + | '''<span style="color: blue">Erklärung:</span>''' <br /> | |
| − | + | Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der rote Graph g liegt jeweils so viele Eineiten über bzw unter dem Graphen f, wie der Regler anzeigt. Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings um a Einheiten nach oben (in positiver y-Richtung) bzw. nach unten (in negativer y-Richtung) verschoben. <br /> Für den Funktionsterm g(x) gilt somit: h(x)=f(x)<span style="color: red">+a</span>. <br /> <br /> | |
| − | '''<span style="color: blue">Erklärung:</span>''' Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der Graph | + | |
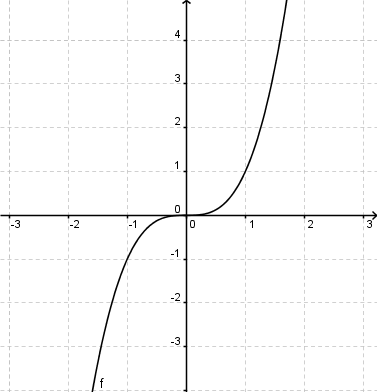
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup> <br /> <br /> <br /> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup> <br /> <br /> <br /> | ||
:::<span style="color: green">f(2)=8</span> <br /> | :::<span style="color: green">f(2)=8</span> <br /> | ||
| Zeile 18: | Zeile 18: | ||
<div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> '''<span style="color: red">Merke:</span>''' <br /> | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> '''<span style="color: red">Merke:</span>''' <br /> | ||
| − | Bei zwei gegebenen Funktionen f und h, für die gilt: h(x)=f(x)<span style="color: red">+a</span> entsteht der Graph h durch eine Verschiebung des Graphen f um <span style="color: red">a</span> Einheiten in y-Richtung. Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten).</div> <br /> <br /> <br /> <br /> | + | Bei zwei gegebenen Funktionen f und h, für die gilt: h(x)=f(x)<span style="color: red">+a</span> entsteht der Graph h durch eine Verschiebung des Graphen f um <span style="color: red">a</span> Einheiten in y-Richtung. <br /> |
| + | Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten).</div> <br /> <br /> <br /> <br /> | ||
== <span style="color: blue">2.Verschiebung nach rechts/links</span> == | == <span style="color: blue">2.Verschiebung nach rechts/links</span> == | ||
Version vom 18. Januar 2010, 18:39 Uhr
Inhaltsverzeichnis |
Verschieben von Funktionsgraphen
1.Verschiebung nach oben/unten
Problemstellung:
Im untenstehenden Applett siehst du den Funktionsgraphen f der Funktion f(x)=x3. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt.
Erklärung:
Der Graph f gehört zu dem Funktionsterm f(x)=x3. Der rote Graph g liegt jeweils so viele Eineiten über bzw unter dem Graphen f, wie der Regler anzeigt. Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings um a Einheiten nach oben (in positiver y-Richtung) bzw. nach unten (in negativer y-Richtung) verschoben.
Für den Funktionsterm g(x) gilt somit: h(x)=f(x)+a.
- f(2)=8
- f(2)=8
Verschiebung um 3 Einheiten nach oben  h(x)=f(x)+3
h(x)=f(x)+3
- h(2)=f(2)+3
- h(2)=8+3
- h(2)=11
- h(2)=f(2)+3
Bei zwei gegebenen Funktionen f und h, für die gilt: h(x)=f(x)+a entsteht der Graph h durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung.
2.Verschiebung nach rechts/links
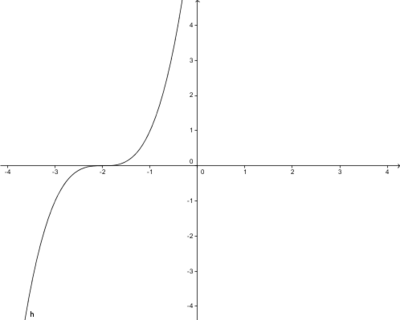
Problemstellung: Nun entsteht der Graph j, indem der Graph von f mit x→x3+2x2 um 3 Einheiten nach rechts verschoben wird. Welcher Zusammenhang besteht nun zwischen den Funktionen?
Erklärung: Eine Verschiebung des Graphen um 3 Einheiten in positiver x-Richtung (also nach rechts) bedeutet, dass der Graph j 3 Einheiten weiter rechts verläuft, als der Graph f. Somit entspricht der Funktionswert von f an der Stelle x dem Funktionswert von j an der Stelle x+3.
Somit ergibt sich der Zusammenhang j(x)=f(x-3).
- x=1
 f(1)=3
f(1)=3
- x=1
Verschiebung um 3 Einheiten nach rechts:
- j(x)=f(x-3)
- j(x)=(x-3)3+2(x-3)2
- j(4)=(4-3)3+2(4-3)2
- j(4)=1+2=3=f(1)
- j(x)=f(x-3)
Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von j(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.
Bei zwei gegebenen Funktionen f und j, für die gilt: j(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).
3.Beispielaufagben
Aufgabe 1:
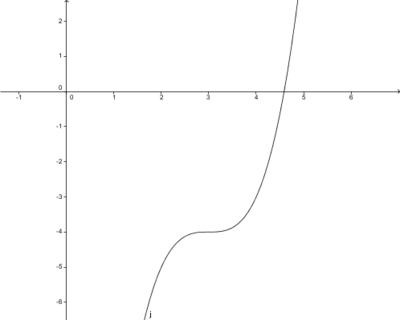
Gegeben ist die Funktion f(x)=x3+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.
Aufgabe 2:
Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x3 hervorgegangen sind.
Aufgabe 3:
Kreuze an, was stimmt. Es können mehrere Antwortmöglichkeiten richtig sein.
Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen