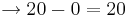Flächenformel: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 1: | Zeile 1: | ||
[[Bild:Integral.jpg|right]] | [[Bild:Integral.jpg|right]] | ||
| + | ===Beispielaufgabe zur Verdeutlichung=== | ||
| + | ''<u>In diesem Beispiel wird anhand einer linearen Funktion verdeutlicht, dass die Fläche, welche man bei einer Integration erhält, die unter dem Graphen ist. Verglichen wird dies durch eine einfache Berechnung der Fläche durch Flächenformeln.</u>''' | ||
| + | |||
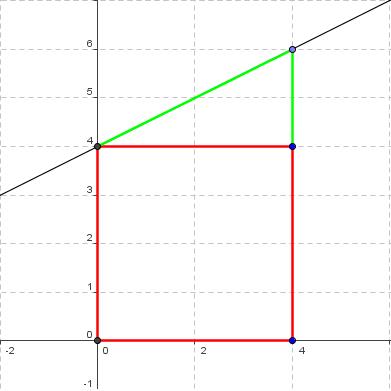
:'''1.''' Hier lässt sich die Fläche unter dem Graphen leicht ausrechnen. Man summiert die <span style="color: red">Quadratfläche</span> und die <span style="color: green">Dreiecksfläche</span> und erhält somit die komplette Fläche unter dem Graphen. | :'''1.''' Hier lässt sich die Fläche unter dem Graphen leicht ausrechnen. Man summiert die <span style="color: red">Quadratfläche</span> und die <span style="color: green">Dreiecksfläche</span> und erhält somit die komplette Fläche unter dem Graphen. | ||
| Zeile 26: | Zeile 29: | ||
:<u>Durch Integration erhält man das selbe Ergebnis, wie mit der Flächenberechnung.</u> | :<u>Durch Integration erhält man das selbe Ergebnis, wie mit der Flächenberechnung.</u> | ||
| − | :[[ | + | :[[Facharbeit Neutert/Integralberechnung|zurück zur Aufgabe]] |
Version vom 24. Januar 2010, 15:16 Uhr
Beispielaufgabe zur Verdeutlichung
In diesem Beispiel wird anhand einer linearen Funktion verdeutlicht, dass die Fläche, welche man bei einer Integration erhält, die unter dem Graphen ist. Verglichen wird dies durch eine einfache Berechnung der Fläche durch Flächenformeln.'
- 1. Hier lässt sich die Fläche unter dem Graphen leicht ausrechnen. Man summiert die Quadratfläche und die Dreiecksfläche und erhält somit die komplette Fläche unter dem Graphen.
- Quadratfläche:
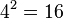
- Dreieckfläche:
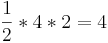
- Die markierte Fläche unter dem Graphen hat einen Flächeinhalt von 20.
- 2. Es lässt sich aber auch durch Integration lösen. Dazu wandelt man eine Funktion f (t) in F (t) anhand der Integrationsformel um .
- ( siehe unten) Integriert wird die Funktion von 0 bis 4.
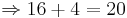
![\Rightarrow \int_{0}^{4} f (x)\,dx = \int_{0}^{4} \frac{1}{2}x + 4 \,dx = \left[ \frac{x^2}{4} + 4x \right]_{0}^{4}](/images/math/8/0/5/8058fe8c427bbc24d407f017e0f4b047.png)
- Nun setzt man für x die obere Grenze ein, und zieht davon die untere Grenze ab, die auch für x eingesetzt wird.
![\Rightarrow \left[ \frac{4^2}{4} + 4*4 \right] - \left[ \frac{0^2}{4} + 4*0 \right]](/images/math/8/c/8/8c8935045647fe58b43d3c98913c8d15.png)
- Durch Integration erhält man das selbe Ergebnis, wie mit der Flächenberechnung.
