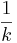Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
'''Problemstellung:''' Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g? | '''Problemstellung:''' Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g? | ||
| − | '''Erklärung:''' Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt. Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f(<math>{1 \over 3}</math>x)=cos{1 \over 3}x | + | '''Erklärung:''' Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt. <br /> |
| − | + | Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f(<math>{1 \over 3}</math>x)=cos<math>{1 \over 3}</math>x <br /> | |
| − | Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5. | + | (Allgemein: f(x)=g(kx) oder g(x)=f(<math>{1 \over k}</math>x)) <br /> |
| + | Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5. <br /> | ||
Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst. | Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst. | ||
| − | Der Funktionswert an der Stelle x=0 bleibt immer gleich. | + | '''Der Funktionswert an der Stelle x=0 bleibt immer gleich.''' <br /> |
Allgemein: g(x)=f(kx) mit dem Streckungsfaktor <math>{1 \over k}</math> | Allgemein: g(x)=f(kx) mit dem Streckungsfaktor <math>{1 \over k}</math> | ||
Version vom 15. Januar 2010, 14:59 Uhr
Inhaltsverzeichnis |
Strecken und Spiegeln von Funktionsgraphen
Streckung in y-Richtung
Zur Erinnerung: Bei quadratischen Funktionen haben wir bereits festgestellt, dass der Funktionsgraph durch einen Koeffizienten a weiter oder enger als die Normalparabel f(x)=x2 sein kann. Diese Erscheinung wird nun allgemein für alle Funktionstypen untersucht.
Problemstellung: Im untenstehenden Koordinatensystem ist der Graph der Funktion f(x)= 2x4-3x2+0,5 dargestellt. Wird diese Funktion nun mit einer rationalen Zahl k multipliziert, entsteht ein veränderter Graph g(x). Versuche, durch Verschieben des Reglers das Verhalten des Funktionsgraphen zu erklären.
Erklärung: Da der Graph von g(x) aus einer Multiplikation von einem Koeffizienten k und dem Funktionswert von f(x) entsteht, gilt für den Graphen g die Funktionsgleichung g(x)=k×f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur das der Graph g hier kleinere Funktionswerte annimmt. Die Nullstellen bleiben dabei unverändert!
Streckung in x-Richtung
Problemstellung: Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g?
Erklärung: Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt.
Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f(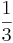
x)=cos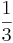x
(Allgemein: f(x)=g(kx) oder g(x)=f(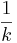
x))
Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5.
Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst.
Der Funktionswert an der Stelle x=0 bleibt immer gleich.
Allgemein: g(x)=f(kx) mit dem Streckungsfaktor
