Grenzwerte im Unendlichen: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
== Konvergente Funktionen == | == Konvergente Funktionen == | ||
| − | Erstelle für die Funktion f(x)= | + | Erstelle für die Funktion f(x)=<math>{6x+1 \over 2x}</math> eine Wertetabelle für die x-Werte -20,-15,-10,-8,-5,-3,0,3,5,8,10, 15, 20 und zeichne anhand dieser Werte den Graphen von f. Versuche anhand der Zeichnung einen y-Wert zu erkennen, dem sich der Graph immer weiter annähert. Kontrolliere anschließend dein Ergebnis, indem du den Graphen so umformst, dass man für wachsende x-Werte einen genauen y-Wert ablesen kann. |
== Divergente Funktionen == | == Divergente Funktionen == | ||
== Beispielaufgaben == | == Beispielaufgaben == | ||
Version vom 15. Januar 2010, 12:06 Uhr
Inhaltsverzeichnis |
Grenzwerte im Unendlichen
Eine häufig interessante Eigenschaft von Funktionen ist das Verhalten im Unendlichen. Man interessiert sich also dafür, wie sich ein Funktionsgraph für immer größer bzw. immer kleiner werdende x-Werte verhält. Dieses Verhalten lässt sich oft nicht einfach so aus dem Funktionsterm ablesen. Es gibt aber zwei Möglichkeiten, Hinweise zu erhalten. Zum einen kann das Erstellen einer Wertetabelle weiterhelfen, zum anderen die Umformung des Terms.
Konvergente Funktionen
Erstelle für die Funktion f(x)=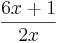 eine Wertetabelle für die x-Werte -20,-15,-10,-8,-5,-3,0,3,5,8,10, 15, 20 und zeichne anhand dieser Werte den Graphen von f. Versuche anhand der Zeichnung einen y-Wert zu erkennen, dem sich der Graph immer weiter annähert. Kontrolliere anschließend dein Ergebnis, indem du den Graphen so umformst, dass man für wachsende x-Werte einen genauen y-Wert ablesen kann.
eine Wertetabelle für die x-Werte -20,-15,-10,-8,-5,-3,0,3,5,8,10, 15, 20 und zeichne anhand dieser Werte den Graphen von f. Versuche anhand der Zeichnung einen y-Wert zu erkennen, dem sich der Graph immer weiter annähert. Kontrolliere anschließend dein Ergebnis, indem du den Graphen so umformst, dass man für wachsende x-Werte einen genauen y-Wert ablesen kann.

