Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
| − | ''' | + | '''Erklärung:''' Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der Graph h liegt 3 Einheiten über dem Graphen f. Das bedeutet, dass jeder Funktionswert h(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Dies fällt auch auf, wenn man die Graphen im Koordinatensystem betrachtet. Der rote Graph h verläuft über dem Graphen f, nimmt aber ansonsten den gleichen Verlauf. Er ist also um 3 Einheiten in positiver y-Richtung (nach oben) verschoben. <br /> Für den Funktionsterm h(x) gilt somit: h(x)=f(x)+3. <br /> <br /> |
'''Beispiel:''' f(x)=x<sup>3</sup> <br /> | '''Beispiel:''' f(x)=x<sup>3</sup> <br /> | ||
:::f(1)=1 <br /> | :::f(1)=1 <br /> | ||
| Zeile 23: | Zeile 23: | ||
'''Problemstellung:''' Nun entsteht der Graph j, indem der Graph von f mit x→x<sup>3</sup>+2x<sup>2</sup> um 3 Einheiten nach rechts verschoben wird. Welcher Zusammenhang besteht nun zwischen den Funktionen? | '''Problemstellung:''' Nun entsteht der Graph j, indem der Graph von f mit x→x<sup>3</sup>+2x<sup>2</sup> um 3 Einheiten nach rechts verschoben wird. Welcher Zusammenhang besteht nun zwischen den Funktionen? | ||
[[Bild:Verschiebung zur Seite.png|700px]] | [[Bild:Verschiebung zur Seite.png|700px]] | ||
| + | |||
| + | '''Erklärung:''' Eine Verschiebung des Graphen um 3 Einheiten in positiver x-Richtung (also nach rechts) bedeutet, dass der Graph j 3 Einheiten weiter rechts verläuft, als der Graph f. Somit entspricht der Funktionswert von f an der Stelle x dem Funktionswert von j an der Stelle x+3.<br /> Somit ergibt sich der Zusammenhang j(x)=f(x-3). | ||
| + | |||
| + | '''Beispiel:''' f(x)=x<sup>3</sup>+2x<sup>2</sup> <br /> | ||
| + | :::x=1 <math>\rightarrow</math> f(1)=3 <br /> <br /> | ||
| + | Verschiebung um 3 Einheiten nach rechts: <br /> | ||
| + | :::j(x)=f(x-3) <br /> | ||
| + | :::j(x)=(x-3) <sup>3</sup>+2(x-3)<sup>2</sup> <br /> | ||
| + | :::j(4)=(4-3)<sup>3</sup>+2(4-3)<sup>2</sup> <br /> | ||
| + | :::j(4)=1+2=3=f(1) <br /> <br /> | ||
| + | Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von j(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist. | ||
| + | |||
| + | |||
| + | '''Allgemein:''' Bei zwei gegebenen Funktionen f und j, für die gilt: j(x)=f(x<span style="color: red">-b</span>) entsteht der Graph j durch eine Verschiebung um <span style="color: red">b</span> Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links). | ||
| + | |||
== 3.Beispielaufagben == | == 3.Beispielaufagben == | ||
| + | |||
| + | Aufgabe 1: Gegeben ist die Funktion f(x)=x<sup>3</sup>+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist. | ||
| + | |||
| + | |||
| + | <popup name="Lösung"> | ||
| + | h(x)=f(x<span style="color: green">-2</span>) <span style="color: red">-5</span> | ||
| + | :: <span style="color: green">2 Einheiten nach rechts</span> | ||
| + | :: <span style="color: red">5 Einheiten nach unten</span> <br /> | ||
| + | ::=(x-2)<sup>3</sup>+5(x-2)-5-5 <br /> | ||
| + | ::=(x-2)(x<sup>2</sup>-4x+4)+5x-10-10 <br /> | ||
| + | ::=x<sup>3</sup>-4x<sup>2</sup>+4x-2x²+8x-8+5x-20 <br /> | ||
| + | ::='''x<sup>3</sup>-6x<sup>2</sup>+17x-28''' | ||
| + | </popup> | ||
Version vom 6. Januar 2010, 17:00 Uhr
Inhaltsverzeichnis |
Verschieben von Funktionsgraphen
1.Verschiebung nach oben/unten
Problemstellung:
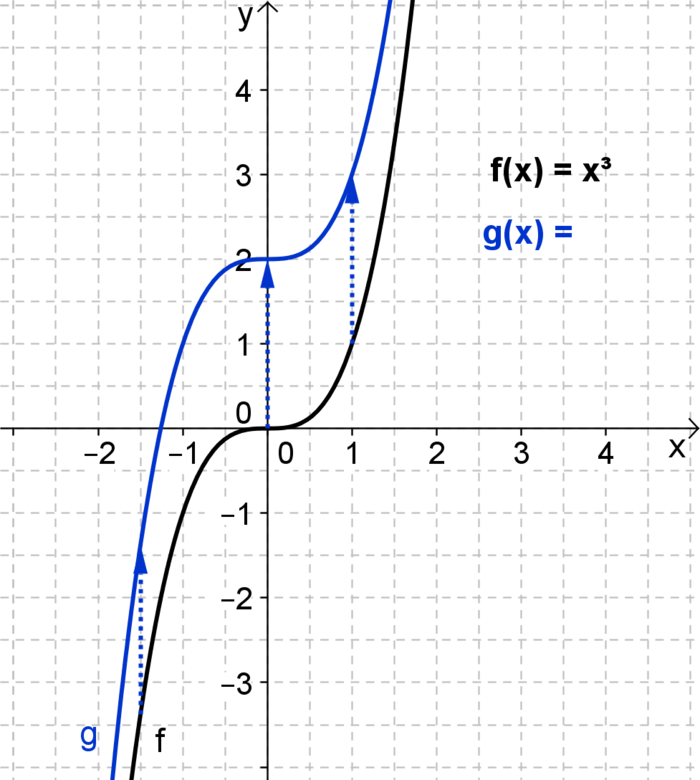 Im nebenstehenden Koordinatensystem siehst du den Funktionsgraphen f der Funktion f(x)=x3. Der rote Graph h liegt 3 Einheiten über dem Graphen von f. Welcher formelle Zusammenhang besteht nun zwischen den beiden Graphen f und h?
Im nebenstehenden Koordinatensystem siehst du den Funktionsgraphen f der Funktion f(x)=x3. Der rote Graph h liegt 3 Einheiten über dem Graphen von f. Welcher formelle Zusammenhang besteht nun zwischen den beiden Graphen f und h?
Erklärung: Der Graph f gehört zu dem Funktionsterm f(x)=x3. Der Graph h liegt 3 Einheiten über dem Graphen f. Das bedeutet, dass jeder Funktionswert h(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Dies fällt auch auf, wenn man die Graphen im Koordinatensystem betrachtet. Der rote Graph h verläuft über dem Graphen f, nimmt aber ansonsten den gleichen Verlauf. Er ist also um 3 Einheiten in positiver y-Richtung (nach oben) verschoben.
Für den Funktionsterm h(x) gilt somit: h(x)=f(x)+3.
Beispiel: f(x)=x3
- f(1)=1
- f(1)=1
Verschiebung um 3 Einheiten nach oben  h(x)=f(x)+3
h(x)=f(x)+3
- h(1)=f(1)+3
- h(1)=1+3
- h(1)=4
- h(1)=f(1)+3
Allgemein: Bei zwei gegebenen Funktionen f und h, für die gilt: h(x)=f(x)+a entsteht der Graph h durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung. Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten).
2.Verschiebung nach rechts/links
Problemstellung: Nun entsteht der Graph j, indem der Graph von f mit x→x3+2x2 um 3 Einheiten nach rechts verschoben wird. Welcher Zusammenhang besteht nun zwischen den Funktionen?
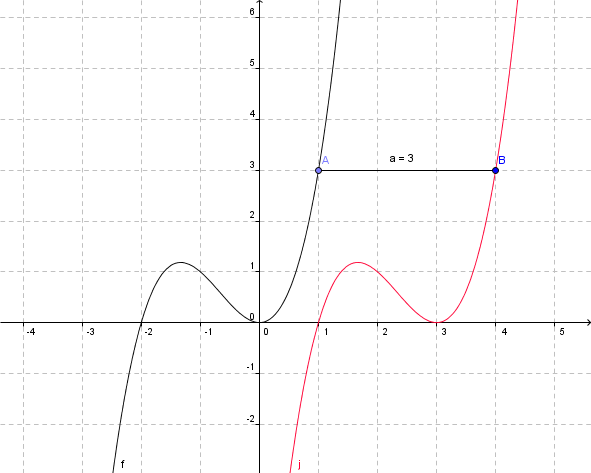
Erklärung: Eine Verschiebung des Graphen um 3 Einheiten in positiver x-Richtung (also nach rechts) bedeutet, dass der Graph j 3 Einheiten weiter rechts verläuft, als der Graph f. Somit entspricht der Funktionswert von f an der Stelle x dem Funktionswert von j an der Stelle x+3.
Somit ergibt sich der Zusammenhang j(x)=f(x-3).
Beispiel: f(x)=x3+2x2
- x=1
 f(1)=3
f(1)=3
- x=1
Verschiebung um 3 Einheiten nach rechts:
- j(x)=f(x-3)
- j(x)=(x-3) 3+2(x-3)2
- j(4)=(4-3)3+2(4-3)2
- j(4)=1+2=3=f(1)
- j(x)=f(x-3)
Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von j(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.
Allgemein: Bei zwei gegebenen Funktionen f und j, für die gilt: j(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).
3.Beispielaufagben
Aufgabe 1: Gegeben ist die Funktion f(x)=x3+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.

