Benutzer:Neutert Jan-Peter: Unterschied zwischen den Versionen

Version vom 5. Januar 2010, 14:54 Uhr

Die Maxima der Funktionen f_a liegen alle auf einer Ortskurve g.

Bestimme die Ortskurve g.

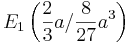
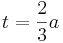Die Maxima sind abhängig von a. $E_1 \left ( \frac {2}{3}a / \frac {8}{27}a^3 \right )$

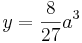
$t = \frac{2}{3}a$ und $y = \frac{8}{27}a^3$

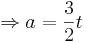$\Rightarrow a = \frac{3}{2}t$ a in y eingesetzt: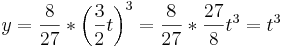 $y = \frac{8}{27}* \left( \frac{3}{2}t \right) ^3 = \frac{8}{27} * \frac{27}{8}t^3 = t^3$

Die Funktion g, auf welcher alle Maxima liegen, ist g (x) = t³.

Die Wendepunkte der Funktion f_a liegen ebenso auf einer Ortskurve h.

Bestimme auch die Ortskurve h.

Der Wendepunkt ist abhängig vom Parameter a. 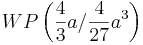$WP \left ( \frac {4}{3}a / \frac {4}{27}a^3 \right )$

Gleiches Verfahren wie bei der Aufgabe drüber.

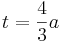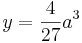
$t = \frac{4}{3}a$ und $y = \frac{4}{27}a^3$

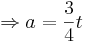$\Rightarrow a = \frac{3}{4}t$ a in y eingesetzt: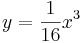 $y = \frac {1}{16}x^3$

Die Funktion h, auf welcher alle Wendepunkte liegen, ist h (x) = t³.

@@ Zeile 39: / Zeile 39: @@
 }}
+<popup name="Applet zu Ortskurven">
-[[Media:Ortskurve Extremwerte Wendepunkt.ggb]]
+<ggb_applet width="600" height="600" filename="‎Ortskurve_Extremwerte_Wendepunkt.ggb" showResetIcon="true" /> '''''f<sub>a</sub>, <span style="color: darkorange">Ortskurve g</span>, <span style="color: darkblue">Ortskurve h</span>
+</popup>