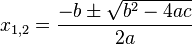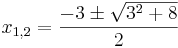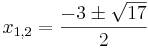Funktionsuntersuchungen: Unterschied zwischen den Versionen
| Zeile 63: | Zeile 63: | ||
Gegeben ist die Funktion h(x)=2x<sup>7</sup>-2x<sup>6</sup>+4x<sup>4</sup>-4x<sup>3</sup>. Bestimme zu dieser Funktion Definitionsbereich, Wertemenge und die Nullstellen. Untersuche die Funktion außerdem auf ihr Verhalten im Unendlichen. Kontrolliere deine Ergebnisse wieder mit Geogebra. | Gegeben ist die Funktion h(x)=2x<sup>7</sup>-2x<sup>6</sup>+4x<sup>4</sup>-4x<sup>3</sup>. Bestimme zu dieser Funktion Definitionsbereich, Wertemenge und die Nullstellen. Untersuche die Funktion außerdem auf ihr Verhalten im Unendlichen. Kontrolliere deine Ergebnisse wieder mit Geogebra. | ||
| + | |||
| + | D=<math>\mathbb{R}</math> <br /> | ||
| + | W=<math>\mathbb{R}</math> <br /> | ||
| + | Nullstellen: <br /> h(x)=2x<sup>7</sup>-2x<sup>6</sup>+4x<sup>4</sup>-4x<sup>3</sup> | ||
| + | h(x)=2x<sup>3</sup> (x<sup>4</sup>-x<sup>3</sup>+2x-2) <math>\rightarrow</math> x<sub>1</sub>=0 (dreifache Nullstelle) <br /> | ||
| + | Ausprobieren: x<sub>2</sub>=1 <br /> | ||
| + | Polynomdivision: | ||
| + | (x<sup>4</sup>-x<sup>3</sup>+2x-2)÷(x-1)=x<sup>3</sup>+2 | ||
| + | |||
| + | |||
| + | x<sub>3</sub>=-∛2 <math>\rightarrow</math> h(x)=2x<sup>3</sup> (x-1)(x<sup>3</sup>+2) | ||
| + | |||
| + | P<sub>1</sub> (0/0) P<sub>2</sub> (1/0) P<sub>3</sub> (-∛2/0) | ||
| + | |||
| + | |||
| + | |||
== Gebrochen rationale Funktionen == | == Gebrochen rationale Funktionen == | ||
== Trigonometrische Funktionen == | == Trigonometrische Funktionen == | ||
== Exponentialfunktionen == | == Exponentialfunktionen == | ||
Version vom 4. Januar 2010, 19:37 Uhr
Inhaltsverzeichnis |
Funktionsuntersuchungen
Lineare Funktionen
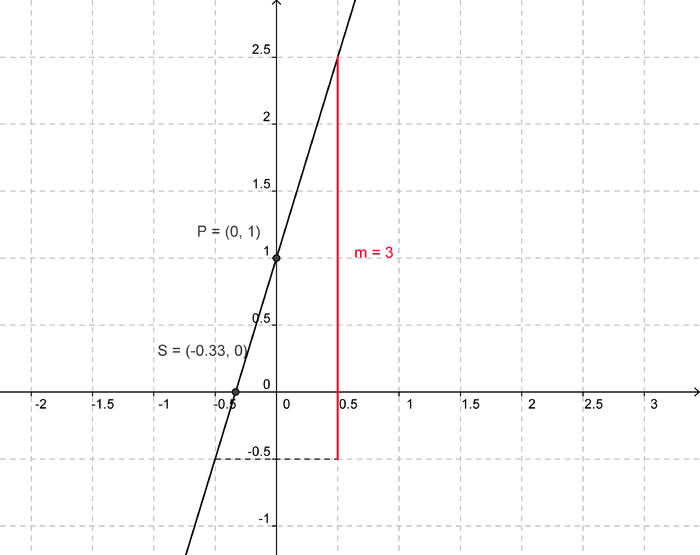
Gegeben ist die Funktion f(x)=3x+1. Bestimme zu dieser Funktion den Definitionsbereich, die Wertemenge, die Steigung m und die Schnittpunkte mit den Koordinatenachsen. Plotte den Graphen der Funktion mit GeoGebra.
Quadratische Funktionen
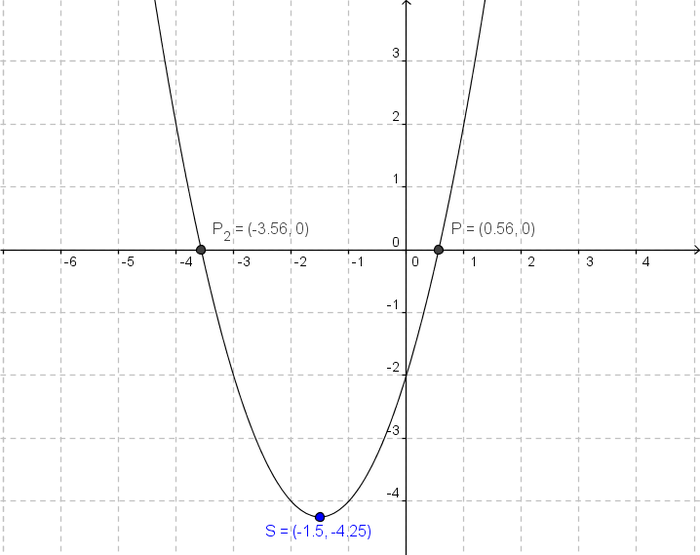
Gegeben ist die Funktion g(x)=x2+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung.
Ganzrationale Funktionen
Gegeben ist die Funktion h(x)=2x7-2x6+4x4-4x3. Bestimme zu dieser Funktion Definitionsbereich, Wertemenge und die Nullstellen. Untersuche die Funktion außerdem auf ihr Verhalten im Unendlichen. Kontrolliere deine Ergebnisse wieder mit Geogebra.
D=
W=
Nullstellen:
h(x)=2x7-2x6+4x4-4x3
h(x)=2x3 (x4-x3+2x-2)  x1=0 (dreifache Nullstelle)
x1=0 (dreifache Nullstelle)
Ausprobieren: x2=1
Polynomdivision:
(x4-x3+2x-2)÷(x-1)=x3+2
x3=-∛2  h(x)=2x3 (x-1)(x3+2)
h(x)=2x3 (x-1)(x3+2)
P1 (0/0) P2 (1/0) P3 (-∛2/0)