Funktionsuntersuchungen: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 33: | Zeile 33: | ||
Gegeben ist die Funktion g(x)=x<sup>2</sup>+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung. | Gegeben ist die Funktion g(x)=x<sup>2</sup>+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung. | ||
| − | <math> x_{1,2} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}</math> | + | <math> x_{1,2} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}</math> <br /> |
| − | <math> x_{1,2} = \frac{-3\pm\sqrt{3^2+8}}{2}</math> | + | <math> x_{1,2} = \frac{-3\pm\sqrt{3^2+8}}{2}</math> <br /> |
| − | <math> x_{1,2} = \frac{-3\pm\sqrt{17}}{2}</math> | + | <math> x_{1,2} = \frac{-3\pm\sqrt{17}}{2}</math> <br /> |
| − | x<sub>1</sub>=0,56 <math>\rightarrow</math> P<sub>1</sub>(0,56/0) | + | x<sub>1</sub>=0,56 <math>\rightarrow</math> P<sub>1</sub>(0,56/0)<br /> |
x<sub>2</sub>=-3,56 <math>\rightarrow</math> P<sub>2</sub>(-3,56/0) | x<sub>2</sub>=-3,56 <math>\rightarrow</math> P<sub>2</sub>(-3,56/0) | ||
== Ganzrationale Funktionen == | == Ganzrationale Funktionen == | ||
Version vom 4. Januar 2010, 19:00 Uhr
Inhaltsverzeichnis |
Funktionsuntersuchungen
Lineare Funktionen
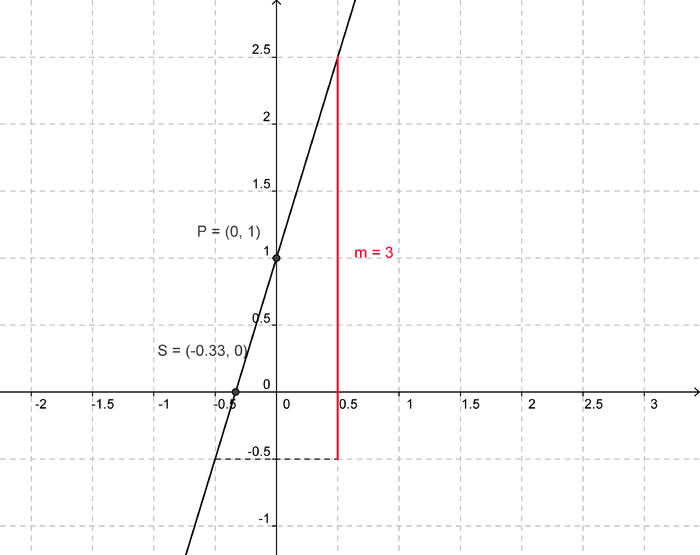
Gegeben ist die Funktion f(x)=3x+1. Bestimme zu dieser Funktion den Definitionsbereich, die Wertemenge, die Steigung m und die Schnittpunkte mit den Koordinatenachsen. Plotte den Graphen der Funktion mit GeoGebra.
Quadratische Funktionen
Gegeben ist die Funktion g(x)=x2+3x-2. Bestimme zu dieser Funktion Definitions- und Wertemenge, die Nullstellen und den Scheitel. Beschreibe den Verlauf des Graphen und plotte die Funktion mit GeoGebra. Vergleiche anschließend die rechnerischen Ergebnisse mit der Zeichnung.
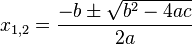
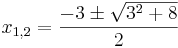
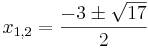
x1=0,56  P1(0,56/0)
P1(0,56/0)
x2=-3,56  P2(-3,56/0)
P2(-3,56/0)