Diskussion:LK Mathematik 2008 10/Lösungen Infinitesimalrechnung: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Bild zu groß)
 
(4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 12: Zeile 12:
 
F(x)=<math>\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx</math> = ... =<math>\frac{a^2}{2b}-\frac{a^2}{4b}=\frac{9}{4} </math><br>
 
F(x)=<math>\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx</math> = ... =<math>\frac{a^2}{2b}-\frac{a^2}{4b}=\frac{9}{4} </math><br>
 
Dann steht am ende folgendes bei mir:   
 
Dann steht am ende folgendes bei mir:   
−
<math>\frac{a^2}{2b}-\frac{a^2}{4b}=\frac{9}{4} </math>
+
<math>\frac{a^2}{4b}=\frac{9}{4} </math>
 
<br>Daraus folgt auch wieder a = 3 (könnte auch -3 sein, was aber nicht mit a) stimmen würde), und b = 1.<br>
 
<br>Daraus folgt auch wieder a = 3 (könnte auch -3 sein, was aber nicht mit a) stimmen würde), und b = 1.<br>
 
kappe
 
kappe
 +
 +
---
 +
 +
Stimmt, du hast Recht, ich habe ein Quadrat vergessen. Ich ändere es gleich, danke
 +
 +
 +
 +
 +
-----
 +
 +
Kann heute die Aufgabe 2 nicht fertigstellen, weil ein Fehler beim Hochladen des Bildes aufgetreten ist, und ich nicht weiß, wie ich ihn beheben kann. Die Lösung ist aber nur sinnvoll mit Hilfe einer Skizze. Ich mache die Aufgabe später einmal fertig...
 +
Gruß Lukas
 +
:Dein Bild war zu leider groß. Beim Hochladen von Dokumenten ist die Größe beschränkt. Vergleiche z.B folgende [http://wikis.zum.de/rmg/images/4/48/Wiki_bilder.pdf Tipps ].  Gruß--&nbsp;[[Benutzer:Maria Eirich|Maria Eirich]]&nbsp;<small>21:13, 6. Okt. 2008 (UTC)</small>

Aktuelle Version vom 6. Oktober 2008, 22:13 Uhr

Warum kann ich keine GeoGebra-Datei hochladen???

Du musst die Geogebra-Datei als .ggb abspeichern. Beim Hochladen musst du darauf achten, dass du den Zusatz .ggb der Quelldatei auch beim Zielnamen anhängst.
Gruß-- Maria Eirich 14:54, 3. Okt. 2008 (UTC)

Sers Baumi, bist du dir sicher, dass du dich bei "2. Berechnung des Integrals" nicht vertan hast?
F(x)=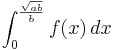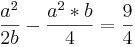\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx = ... =\frac{a^2}{2b}-\frac{a^2*b}{4}=\frac{9}{4}
ich hab hier immer:
F(x)=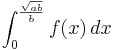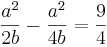\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx = ... =\frac{a^2}{2b}-\frac{a^2}{4b}=\frac{9}{4}
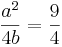
Dann steht am ende folgendes bei mir: \frac{a^2}{4b}=\frac{9}{4}
Daraus folgt auch wieder a = 3 (könnte auch -3 sein, was aber nicht mit a) stimmen würde), und b = 1.
kappe

---

Stimmt, du hast Recht, ich habe ein Quadrat vergessen. Ich ändere es gleich, danke



Kann heute die Aufgabe 2 nicht fertigstellen, weil ein Fehler beim Hochladen des Bildes aufgetreten ist, und ich nicht weiß, wie ich ihn beheben kann. Die Lösung ist aber nur sinnvoll mit Hilfe einer Skizze. Ich mache die Aufgabe später einmal fertig... Gruß Lukas

Dein Bild war zu leider groß. Beim Hochladen von Dokumenten ist die Größe beschränkt. Vergleiche z.B folgende Tipps . Gruß-- Maria Eirich 21:13, 6. Okt. 2008 (UTC)
Von „http://rmg.zum.de/index.php?title=Diskussion:LK_Mathematik_2008_10/Lösungen_Infinitesimalrechnung&oldid=8515“