Benutzer:Kirchner Nellie: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| − | + | [[geogebra lösung.png]] | |
| + | <math>\int_{0}^{4} f (x)\,dx </math>= <math>\int_{0}^{4} f (\frac{1}{4} x^2)\,dx </math> = <math>\frac{1}{4} * \frac{4^3}{3} </math> = <math>5\frac{1}{3} </math> | ||
| − | '''A''' ges = 32 - <math>10 \frac{2}{3} </math> = 21 <math>\frac{2}{3} | + | <math>\int_{-4}^{4} f (x)\,dx </math> = <math>2*5\frac{1}{3} </math> =<math>10 \frac{2}{3} </math> |
| + | |||
| + | <math> A viereck</math> = <math>4*8</math> = 32 | ||
| + | |||
| + | |||
| + | '''A''' ges = 32 - <math>10 \frac{2}{3} </math> = 21 <math>\frac{2}{3}</math> | ||
| + | |||
| + | |||
| + | [[Lösung Stochastik : Übungsblatt 4,Aufgabe 4 b)]] | ||
Aktuelle Version vom 9. Oktober 2008, 15:36 Uhr
Hausaufgabe S. 216/6
Berechne den Inhalt des Segments,das die Gerade mit der Gleichung y-4=0 vom Graphen der Funktion 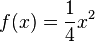 x
x  R abschneidet!
R abschneidet!
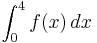 =
= 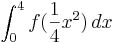 =
= 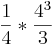 =
= 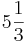
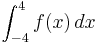 =
= 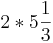 =
=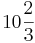
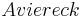 =
=  = 32
= 32
A ges = 32 - 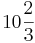 = 21
= 21 

