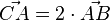Abi 2016 Geometrie II Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 45: | Zeile 45: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Gegeben sind die Punkte A(-2|1|4) und B(-4|0|6).<br /> | ||
| + | a) Bestimmen Sie die Koordinaten des Punkts C so, dass gilt: <math> \vec{CA} = 2\cdot \vec{AB} </math> <br /> | ||
| + | |||
| + | b) Durch die Punkte A und B verläuft die Gerade g. | ||
| + | Betrachtet werden Geraden, für welche die Bedingungen I und II gelten: | ||
| + | : I Jede dieser Geraden schneidet die Gerade g orthogonal. | ||
| + | : II Der Abstand jeder dieser Geraden vom Punkt A beträgt 3 <br> | ||
| + | |||
| + | Ermitteln Sie eine Gleichung für eine dieser Geraden. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Aktuelle Version vom 27. März 2018, 21:02 Uhr
|
|
1) Gegeben sind die Ebene E:2x1+x2+2x3=6 sowie die Punkte P(1/0/2) und Q(5/2/6). b) Die Punkte P und Q liegen symmetrisch zu einer Ebene F. Ermitteln sie eine Gleichung von F
|
Gegeben sind die Punkte A(-2|1|4) und B(-4|0|6). a) Bestimmen Sie die Koordinaten des Punkts C so, dass gilt: b) Durch die Punkte A und B verläuft die Gerade g. Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:
Ermitteln Sie eine Gleichung für eine dieser Geraden. |