Abi 2014 Stochastik II Teil A: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
<center><big>'''Mathematik (Bayern): Abiturprüfung 2014'''</big></center> | <center><big>'''Mathematik (Bayern): Abiturprüfung 2014'''</big></center> | ||
| − | <center><big>'''Stochastik | + | <center><big>'''Stochastik II - Teil A'''</big></center> |
| Zeile 47: | Zeile 47: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | + | [[Datei:ABI2014 WII TeilA 2 Grafik.JPG]] | |
| − | + | ||
Das Baumdiagramm gehört zu einem Zufallsexperiment mit den Ereignissen C und D. | Das Baumdiagramm gehört zu einem Zufallsexperiment mit den Ereignissen C und D. | ||
Aktuelle Version vom 10. Juli 2017, 18:42 Uhr
|
|
In Urne A befinden sich zwei rote und drei weiße Kugeln. Urne B enthält drei rote und zwei weiße Kugeln. Betrachtet wird folgendes Zufallsexperiment: Aus Urne A wird eine Kugel zufällig entnommen und in Urne B gelegt; danach wird aus Urne B eine Kugel zufällig entnommen und in Urne A gelegt. a) Geben Sie alle Möglichkeiten für den Inhalt der Urne A nach der Durch-führung des Zufallsexperiments an. b) Betrachtet wird das Ereignis E: „Nach Durchführung des Zufallsexperi-ments befinden sich wieder drei weiße Kugeln in Urne A.“ Untersuchen Sie, ob das Ereignis E eine größere Wahrscheinlichkeit als sein Gegenereignis hat.
|
Das Baumdiagramm gehört zu einem Zufallsexperiment mit den Ereignissen C und D. a) Berechnen Sie b) Weisen Sie nach, dass die Ereignisse C und D abhängig sind. c) Von den im Baumdiagramm angegebenen Zahlenwerten soll nur der Wert |
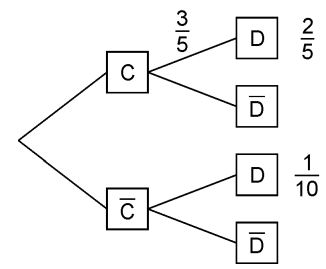
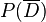
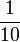so geändert werden, dass die Ereignisse C und D unabhängig sind. Bestimmen Sie den geänderten Wert.
