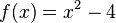Q12 Mathematik: Unterschied zwischen den Versionen
(→4. Geraden und Ebenen im Raum) |
|||
| (27 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
===Abi-Vorvereitung=== | ===Abi-Vorvereitung=== | ||
| − | + | Freitags 5./6. Stunde im Forum B0.03 für alle SchülerInnen der Q12. <br /> | |
[[Q12 Mathematik/Mindmaps|Mindmaps zur Geometrie und Analysis]] | [[Q12 Mathematik/Mindmaps|Mindmaps zur Geometrie und Analysis]] | ||
| + | |||
| + | ;Abituraufgaben mit Lösungen G8 | ||
| + | *[https://www.isb.bayern.de/schulartspezifisches/leistungserhebungen/abiturpruefung-gymnasium/mathematik/Angaben Abituraufgaben Bayern] | ||
| + | *[http://www.abiturloesung.de/abitur# Aufgaben mit Lösungen und Video (kostenlose Anmeldung erforderlich)] | ||
| + | *[http://www.mathelike.de/ Aufgaben mit Lösung (keine Anmeldung nötig)] | ||
| + | *[https://de.serlo.org/mathe/deutschland/bayern/gymnasium/abiturpruefungen-loesung Aufgaben mit Lösungen (Serlo) bis 2015] | ||
| + | *[http://www.isb.bayern.de/download/1766/das-abitur-im-fach-mathematik-am-achtjaehrigen-gymnasium.pdf Handreichung des ISB] | ||
| + | *[[Abitur_Mathematik|Aufgaben mit Lösungen von Schülern RMG (im Aufbau)]] | ||
===Hausaufgaben=== | ===Hausaufgaben=== | ||
| Zeile 15: | Zeile 23: | ||
[[Q12 Mathematik/FAQ|Fragen und Antworten]] | [[Q12 Mathematik/FAQ|Fragen und Antworten]] | ||
| + | |||
| + | [[Q12 Aufgabenübersicht|Aufgabenübersicht 1.Klausur (EIR,HET,SHE)]] <br> | ||
| + | [[Q12 Aufgabenübersicht2|Aufgabenübersicht 2.Klausur (EIR,HET,SHE)]] | ||
===Kurse=== | ===Kurse=== | ||
| − | + | 2016/2018: [[Q12 Mathematik/M1 2016_18|M1 EIR]] - [[Q12 Mathematik/M8 2016_18|M8 SHE]] | |
| + | 2015/2017: [[Q12 Mathematik/M1 2015 17|M4 EIR]] | ||
2014/2016: [[Q11 Mathematik/M1 2014 16|M1 GRÄ]] - [[Q11 Mathematik/M8 2014 16|M8 BEK]] | 2014/2016: [[Q11 Mathematik/M1 2014 16|M1 GRÄ]] - [[Q11 Mathematik/M8 2014 16|M8 BEK]] | ||
| − | |||
2013/2015: [[Q12 Mathematik/M1 2013 15|M1 EIR]] - [[Q12 Mathematik/M5 2013 15|M5 OBL]] | 2013/2015: [[Q12 Mathematik/M1 2013 15|M1 EIR]] - [[Q12 Mathematik/M5 2013 15|M5 OBL]] | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 67: | Zeile 78: | ||
<ggb_applet width="648" height="588" version="4.4" ggbBase64="UEsDBBQACAgIALigQ0QAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ1V4B1BTURMuIEqkCKGE3hKiKEFAioJIDZGiSEkgVCHSpApIJ1IUCCUKCohKEVBKKBI6CEgLSJUqJXSIIL1JF178/3/em3dn7rkze+45e3fv7p7v22gD/bssjHyMNDQ0LDracCPqs5l6fwdcoI61gSqmNDRcRzpwdaT/+JqV2RPOkZpf/RvP6iim36aQ1sXzBOXJbc1OnTGuN6MGzzwVUZ6G++Mzrb6pbM9lCmglAWHvtLXRTjfHiehyNvpmETH83vkXYmJhcfFsDjJtXdENHL0LTkN3BmUHJwcHd/6irAYHvYcyao+DF0/Ih0FJJSIrP4s4wtTUqkWnnx0XPdHDacGgBVny1QE7Of6/3jm2xko1iDs4Ogp+G73tt17t+yhaC9YFF5eS4nYZKU4Su/VkJhRtacnJKqTMxhmTYZeUhPBoOMw56e7u5oxiFQapnmw+f3TWVx+0b/nVHwOUuA6WU1CISU0VmEJjPt8EjpPJpKEhzkVD3cAChFwDLqmyrZQM/7jyCt3RuC0AbDg7DcIAu3xgBEQrGORIjwHGKtARcVrDOHTrthxQPNEOt4hrzBMnvg7TArPFopF4cU6+rlZwsl+02ogwVUoK5fvf63NxajBMP0IERIQBbTEYjfLycgN5sElgHiJP1/YyiUTKqqw0qdtq48+Evn8Y8rdiQuRW5DcGY+KrB8FVBWt/j/c13RYXFzXdPCaqRckYArNH7COnWAWCZENBpdNiROXyuCfzSNb4HM844fhTlc/xKblfYaDsRmBxR6BJjmzzwsKn0WrP7BVZuuysVt0LIGMY1c1NnEwxLOHLl3MfZOj/drERaFpEj3x5+FawIjfX0eyD3tvr0cIhJ/27An0FSWX0AyMjV14KqzbMeXCCXDsSFZLrEfS1p6uk8VL72NEqj4yJjPR0EBMT07YfT/Tw8HDO4sHJzg/7xfYLVyUkLHytfa4/1S8/P2Z0KBT4EjCN3RckurYqBe7miUtKJh079qYmCJp33BXGiqlGRUa2jpU5UhQUFEDLB30dMkxqyysrpKn6IM1vBd6HFCEj+W1FkJKLtXX6hKrvaspqn7NdT0+PPJQOcagZdalj7sdib9ob/k6sxvDADwoiYrcciU+9NDZd6yPxIuF6PqCEtdiypnR1tLExVEwNtihTejUFMxsvZuQlFCjx1LzMeVJeXt7L7rn7B/HkDyP2DMm1Dli1zRYfQ/kb8WvkKr1zJUVFknLLmTsSd7gjIciI4uLrBNvWbQUgO7Duu52dHVzu5s0oHE2VUOeYZgkr+KmfH1NniNgEyvly57MSzNDcVO5r/5cAv40pn92T2vEFuX9KIiN6+fEHtQVyRo7tInQehuUrzYoqBzPPE2uj7hE3qca+Wk5ETIkONyUVIAMi4hZmmp577Rk0yaZuLHS8kehl8AwHPE7CZAZdTsfumW1R3f41nPLLpya6wnuxNw/eZ/X5rdRDhTtSE0VQKPTGtaLeKF7wSbBBrHUAhYtcr6w/pfkDKKqq+tB1vFzH/cGdP4n+R79zNafXpvrUU5X8YOjz58/r3LyGysXLQfrQDjHnicEvSZxMmI5LkeLEd8tho0xIcHUO6kQ9X6OlpSW5XsfBOg9dZ/hYk/6ocY0U7skkqPKaEwRC+GRcuz2/t0YeeGmQz2VgT/wyvzpVbzHOSpB8pmnHnyHtD/wdeUWPcmfWuOKzcyLiQuEHtHZii9OXgatxzA7l6osnywVfsthp1fXEVvLhKsFZkJVb2rvPezLH3cmV932fdl/j4uIq1ZwPVgIiydr7V4viKE91g56cY0pjjnUYcnKD0z81qNNWeR2ThQutfFJG0A9e+A6s+TL/kQVxsllpQFSjp3QMRH8cv7wilGOlhkcn1CN+B7LWIN9ozP7fzK3Tow/E45KYC9mANhRIGCM78wWKUZ0dW5gnPQZ6ziWJ0aIFG9F7ttQPeffj1Z98Nju+Yut6pd0HIiJZpTSe91DwRhWVrTsJlTghQqWzsJuMJKGyj6sfBIH7WwhoWnx+MMcxjbIoH5QprMRT6hBuhssGHgXFgu1PJAmSL2c9hrEDZPP6XG9v72JlCUAJuAK/WxiX7vIpKCZoaaiMsQewtIlewA9bbP4BDxpQ1mVJ4ehn7eYOkJPdwQeZWCwtEyp7iGSklW7Y9bNnJQZpOa5tkGjaMd/+yt7WGjodvHMfoOeRyyijHHxgsH4Fo9mH3pMxCQioueU59+JeSOONn6enzxQb1VFN72k5b6uNy3uFfrw485XQgMcuMOTrTs5ODyvGDVT6WEoYmZldNZYf2tY/yeDl5WVn4CpQPVzgCBB4H+Ocy41RQwrsSQJm+cF9fxyFk5dxx/sb3Ld9V+OXpbZDFVxHRX4WW0lUuk9eu82nxM4+pQaCjcC3zn1St2m6ND6v/B8luI/zzb+Y325mMRq0qMNSHz6GaE+0dNM0nZ3v6O5mrhhkkgm9NTY2lrnXIEL3XH3PVvTipWxJJXYlkNIl9hVpQhbkWhSgU959qs6sklzm+EqMbk/9ZSy3VOffzY1lAZ6kFq12FF14PvMIVQELC4uX58BwgamWsfEbMcFOJKacwXA6cEVSkcMWYbC2q8GcnZ29fcRuqPoOM+ttWCk0BJ28MISSFxgJKdOcZPoiGQG8bVSEKiBkT+nb2lyWLrAn8Yah05ubV4EA+jlwKv+IFn8YutgWuixtQ02suWYja84rI0fvrUwLR2stOLMsc2oluNpnLpNq+q3PX/qz1yBKNw/Ys23qomvy0q2/DtOtagRUtOBjqB9euzTaLzaBJXy952N6jdnHP8vG8uFX3/vFTs9NdT02+MF5S6I8xTkaWKQMI7MZr490zEfBp0jKQCwoX47/s0ggyi0be1LEV19oo+jJWlZaunBlIjvQCs1TfCC89iS74e8eeVvgaEngpeD1/olcNorngFV+9XU2WjplTgFjhaj1zG0u4ObM5se+LeIJ6ycnNzeWO2JYu5aNpU9paWlefCzCv0Wqw/xxPFubbP0XOiIIeKW3fGNgvFGgdLtryJMn0nKB0FgAwBWFQkXX1tba+9huhTSdfxzFX5GXp51+bt+IW9DCL+0aGO6VsXzdeDIpcLY5gi1gRoF0hlMIDJrORwBSgg9mo0QrN8Yr9E4d5Epn/e6RbkUCHh1oMzS1XKCdwu5bHYpQNb/4p1mXBSen+7tJoAyr1WBXYOugJ53knpHHj4IW80Y3v/ylVOGs+XskYi+avs+oDd3WczvktE6Ato9WBiPyEUPdmicHc8KCSNxM0Mdvfi/G/hk2pbQg+JUFhhFpTEqPyw11WX+lrD13PcLsPvWlG51V8jmqNerEOj+FDMk8VakTsbr/ysTd3N9wbPMbkU/6Bjn3eGhKv/saiIoabLiYGEme/6k3F3PQVDwxJUZnrUx7dqPSpkTi6cQ6DT+9+pdNEQsw+8W3+ZCpNipCmSEgw+t8ob7nR3dHfoAxvEJ2g+c8l4Pjo6OjDWj007KrqkxPv20iZzfAs2B0khOhBGX7PoYVR3N2x/r+i5SwmE6NVUCJ6I3Cb89AxKhNkQ9COOPF5yJGde6Ttfb+KYZs0djFNL+FadHLtpGxtyKbfcyr/acZ4GqO6qRfIQzZpxyhRInGHOri9pbnroEi+mms279zM3TBGJDhotoAt9fjeHTOaS8zd5hSRFevDhieFB3tMnda/9UraHfJtlvpEYxWITv/JywvJyvLob/fqRppmsfX3wcxWebpCuxo33RVr30QTfGDtbx+FVj5kQwVBsp5FixkX/uyhOi4m6frnhSc+u6dJ8VMPZRi0nF3QtNUTyXSkekGKXzOT0byMG/l0T2iSPI0MQWjTq3gLnAYJiARsBvGIcGLTreqewDD1ERTFMG3zOJi0K1ZztTpfvRlENEoDjCbBKXio5sl1Q7v0K3shRj1zL5/M8p69DkMt5775FZawH7uj9f2oNK5uU/3GqTWMxdxNiblyehoW0mkT2y7rJ8ref2VPq4p6xzG5kGy1LooKluuqfQNQEQ9RL2ymnxTrNbPwUDeSyNFaIY52QpOc/GCyo8kscaf3262c+/HXwU9DrdnAK6/iut6N6P/IAQHwAbtHc5RoU+Ws91jC8vlk/qAIE16A34URFeX6lWai5F6Z8Rw+tHIsksHc6fSJPD9kjloc0+ZY+sTncZ4+tFAlZ490h0xoPYLnFho7FAcvRgdaZ/QH+z4ttrEAphAj8Q7NR6No9PdFaE5Hx5oQWnx9gwR68aOJYXstif+SdX945ho+oanGctQYcNpwBed+xeAVNTEnMwFZhYYk3KvTCPeo3M9x3uM9WRl0VPJGrCytc1UXvftuIuK6ce/fuX/4asFVNjR0dFK4jDP2j2rKu2aM8d+cU9M1Bvvub2+TyetfquqtSpXwgPeYep+l69ODK69bS3qUpeZnryyvxW9Mdq+cVPKt5PlmLtq9WnRAmQ9swAqfFtJaYFJeojf+hbkwA/h/8TH3LJ3SgxUGy7TQ9/wAbgr5VBx9hhyMIhQmzIYOX01f5nWGLbUoRPwpV/D0YCZK6QS5iGejremejBa/8W7nDeG5+xNbrYBBdgRyWlNRvCUk1LEvXTXkgj6OFiZd44YMFJvBxMDjAcg8a/Bfg9YcB7vowTHrlmfGsgJO7O7UbIr3X2EOQ3ks2hdpH5OcpyrLARrutq8c1yaUTDcMv/Mo3rb9dikRkXtkeKwpZ11eym13CV2tNZ0pXmZQZU1uVycBUU1hjO2sVt1aFKzJtoXSGs4398JmeskZsVf3+AEOp+mbsQuag1/jyIYPlAvPjhqjrBHFBnDPzq38jZ5yzZjznCWpsojngERflGydG4vykuA7pI9NH/v7ukF0Vz0cgeGKdChID/yENoZDSYhsKHfqGRxVDbnZQ0lvUK42i9xI6j7wzpO+U0KVdW01C6p3tFuTBNNZKNlWgnakWV+82vInPYmbpMUGXIwF5AAuKpND8tNVbZNl4KDDeS3K5zpUXlSqrK/KInUWIIdt6HTH7uBIJ8Pk3+y9qFzjoferg9mZmdI7jBqkZdU/tACeQwsrL2fzmi/TNlYitNhacYEXRjK4zvUkOfzONBg5hKOccHToCC9gKuqENjeJVxDi5mEV8QtiDSp2Rsdi9cTXBuyuUe21JR2/kAw9YbPpxt55rjKZRblOzmRiEXfVO7yhxES6tFbyOSf3F080C6WtwvRhJFt19+pWHyaxEu3Yx9q7kjA+/RU9vb2Yo6Ojj6xiXK19nLv4IcTJd0+G2HzA+o7E3qXxYDBHHelrx3iGP0YWIUS2yevH+Z1qtQabhv+BbnwqrPZPjuorQ76E+kvJy9195iBo2rhsp74dcEWDyeIaYwktncPL+kStBP8tTqxDNWdrnoF0iTLrSQGlH7Pmr4ONDVnWDh10vvG477Mgt9+nltLyUE8O8kZp8LA2y5k0/LJ7QLZSLdHil8MyaVnt2fMO9prahT99FTWqbj52YO2uHjGq6CtboAfIpdyZTnuktCYVBvLHJ1vD4DwplYGcnCD1MwEFf5byHe/KhUE4YrIgYLy+aCG8lnEVWUgG89KZ9frx+wJE+m+wLC2G5O5xTZm0OYqjrLSBvEhkexyhlwcDXZKEtyHfd9GKy8BT1GZFH+zgAx8YRjfdRXcWO0TC2DOo7KiEA5K/w+TPHXEY1YknvoH3RFqBoVSUi270OBUIDU1xxGhgtJGvui4ERO4pYQaf5hCuBQKMsQpKCkVz0WZs4JpDuMICfNzSPvfEVJf4b89poBXZCVaxwZELST0Ng56zNqAPHf9B8IyXpA4rjTb7FZ1qeqElZTaXmjUJc7OhYo/5Dj+PhmS1VXR6/yCMhpXIhrvhYVAcTamPJOMQOS4ZvmNGE0orYy5IY9R2FzH2k0qJyCUUV1DPcTYEy2oQ+qYh3Fug+WN8B0SXDNJMtay7VRxgQ8YVyKww1dv+m+3ojh7Cbi0OUR6cFxsnobj4c9Rcz7S91AfQtkANbTlLoPzuJ0/WvcNL7MrnutOd/P5hIhP0BvM79Xdz2fFhSp7VuGkyc/UG2xY6XGUz+QtNtoVxglwODD5EfyJzEcH0+mPzrt2u8Jfvli+p40hJR0tV4PajamVfqF6lAsxEh1KkjZtEGdPG/ugFdLUEL/frjv+3Aou/f/saCxVtEC84sBiloc8gcyr7PUBvJg9S3LMpTvk/jU+YMnJgPx+Pm2yt4KGdecflgfss/o+VffMDMhIalhtEF2rJKRiZrtDl6YTRDsfHn3II1td4WMqTnEfZjgGn7pXYrfnFAkIJH41iTRuo4ESYduKKNgx/8uNqRZjI3BaHR8RE/VMnyzX3SNqq4PhekGhDSHZFWbLJ/72A9qP0zPb2xmBhZ/ujA7np2CaOGNTcKE3xGe7BK+8NO2q0rrAusZuVUOGHR4VsTXFTLmbRn3Gzwjy2wYHW/5jITAYDH4l3HqzSxJsU/5tckyyOMM1vuHvTGZa1saTXwPMfZxl6i4RAJMBodXlEipT1o/RCgr6iv72rN7/5MDzKXjp/DeFv8usMiNHcZU9Iw9B2QzbcJKHXwwHb1KWp8c7p1EhtoqvnXCXDoPmP6pFn+QsZGzWlkvkkusfwd6+fRtbWAiTUVTkTQMQZrjp4bhFyoisZC7J7tHkaxkLybblTgq/SNDO3kmQlulfmd8DhZYWHN70P4t7+aRMlNNiEuw9EMnqMWNjZkRGQSHCq7G9ZiYp3NuzFZatkcWfLyrxP4pAwmc/zq67ScHWzk47Fjdakz8/CglZt695pbBxNnefOMu9EX0WcrqRQw46+0s86JI64xmfOj1c6Wpo/1p/XLZmSG6NtadMbNmQvK0L0L5pt4MtznZGwHvCt2/uan39UePQw7c1oCdlJpu8xVoN9fHxoQJMF7S9vb2XCW7M5RN/v6/uJ+cJfUxmN9Q9kh+NxWKzPn8mcRXaSIu7KefaYzDN/S6M7SVfPZBIpDZE2QG8hChPw5jgyRf7ic7OznDqES+BpvKsrNraca7CX78cEt68me/UtrK0XOWLNMZC/ruAPZ+v6g1aUFAQs/OrZ/vCbfz5gfN0tIOYLl+M7aeunh6f1drExp1Sz3mEqXTqKr/n+aHUwHj9tBE9tP71m8ztXu/pn7FPJ3tnGhi9B/w+afbEQFljk9ap4IyA4Iy5Gx3PuGEAST4r0f7XmiMAIzQeUQHb9nXg0hHE5EbJwbL4f8RE3D/a1ZqFpwJrQ3kwlcjr0zNCeZu/3yDi/v++Xe7/+nZcYI1PtRrMecCuDXRBYGBg6+hoymMr0cRedH2gj5N5eFNWHEjgnN4WK0Y44yBd2yLY1M1wxahCS+fJMMhnux/EJdpM/teLMz86aPUbBq0hLRLPV40rJO/wVWhh79cX1foKtFTkVd6K/Iba1/Fw+ZOuf/9+zXahSGPM0H/bdgnrV9czjX84c12aEY5BmuJk6YjBqpClh93Of/sQIibjo4BdPmCsNYQVGKahEyldeg+GSQC0gkEoCGNEG9UsymMqwb5baGcT8BKgX6eY8D+A+xkMTBFS+69YO5TqiYm2I+5ag93uzK09HA310tHShxdr2IT/H1BLBwjlzt06ERYAADMWAABQSwMEFAAICAgAuKBDRAAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAgIALigQ0QAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vl5bxs3Fv87/RTELFAkW1viNYccKUVToNgAThPUyW6xm90FNUNJrOfqDMeW0/S795GcS5Lt+Ai2wNqWOJx5fPf78XE8/3abpehCVrUq8oVHJthDMo+LROXrhdfo1XHkffviq/laFmu5rARaFVUm9MLjE+4N62A2IdgsVsnCi0O6EqvEP+aSUfgi8lgsmX/MuKBUzPxlglceQttaneTFjyKTdSlieRZvZCZOi1hoy3OjdXkynV5eXk466ZOiWk/X6+VkWyceAs3zeuG1FyfAbmfRJbPkFGMy/fn1qWN/rPJaizyWHjJWNerFV0/mlypPikt0qRK9WXgBjzy0kWq9ATNDHyZTQ1SCraWMtbqQNSwdTa3NOis9SyZy8/yJu0Jpb46HEnWhElktPDzxKQkwn7GIhvbCQ0WlZK5bWtLKnHbc5hdKXjq25spK5HgWQghUrZapXHgrkdZglcpXFXgUFKoamNb6KpVLUXXzQR9yBL9AoD5KwwtC59wAT0KKj2hAjyKCj3wfO2XGkj2kiyK1bDHyZ+jTJ0QxxejIDMQNFIYgcI+wu4eZG6gbuBt8R8Pdcu5IuaPhjoazWwxt54Ol7Y0dUztD2Y6hGB+ZTwAf64E9O6ORncQY8QkRo70dGDJ6E6u/GXg7Ddw0tAPBbiDtw8h8WX8Fj7SIPcgiMpLqEuJmoQcJ00kMWHh3ifRRdg5WsuhQJvVvsPKRzu2EEn/kWpBl/+znQCS7l503uvYeEgP+mOJ/gMAQ75R9V/NuJO14mxu+mFLzaQeH81YhVG8MbZvSWma1UZHNLDghgnwo3iAELPERmcEQmiKmiPiI+zAlEQrMGCJm6pYjhiJk6AhDFoL8CL64rekA+cDL3AxdcSPGkc8QscDFEXgBWfADn1AGFL6PfFhkpBMjlgWIBzBhEeKgoIG90EALg3UwB+EUMYKYWUtCRAMUUBQa6CTcIGoQGd2BKUUBRoFZCtgJuOkwE1ZEiBlroArKola9czcyLfuoWD+qvGx067v2fpwlnR91sUeeFPH5yz1nS1Hr7hqIYMsaNka3he3sm0/mqVjKFLqLM5MHCF2I1JS55b8qco26HODu3roS5UbF9ZnUGlbV6BdxIU6FltsfgLruFLS0cZHXb6tCf1+kTZbXCMVFijvl4JqMrulgcZGy0QM+fuCPHgSj6/BauQU8QU0tQX5R1R25SJJXhmLAAXDfmzy9ellJcV4WateM+dR2JXPZxKlKlMj/DrlupBi/oL5JMRjcNSmBH3SKFFVydlVDAaDtP2VVGGCaMAI/LKSM+7MI8uDKPfEpmwRs+PVBs1iYwuWcTIIwYtSPQj7zQdLV9U+CqI2SvOjjI7ayN31dqWR8/ap+WaRJ7whr+/ei1E1l201A+8pY9F2+TqXND7t/QOMWny+L7ZlLDOZ4vbsqYYad/OXa+hwBqlAfDFm349KNlsYo1lNhS4MtBe4yTSX9czKjlsKOSzdaKkhdp1prKOusJLgTo2qLl9jbKRSb9wtv66EmV/rUzaDIVHzemkrcgh+bbCn79NnlSa7leXV/nvPpXn7Nz2WVy7RNZwhlUzS1q85RpkNyvxV6812e/CTXgCtvhYF2Dawd6aByImOVwUJ3vwuBCex7UNXdTeS6kp2Jqe3wnWvtUzzO6YPbltUPVZG9yi/eQdbsqTqfdvbM67hSpclNtIS95lwO+ZeoWsBOlYzXmUoFK2KDmuBIbZwINdzoTVHZJh6gB0ZToNuykrU5/7g4IGADeLg1oPl0+wwt0FNo9NFf0fY/T+mzZ5a7TGUGbT7SNnlXTW7l9IFc2SOECRgqlr8AaA7dSUswhAII+mz1yU46I5GWG2HOGa2zUnElqx33WX6vi2TfqRAzazlASGkYmPwppXSpp9uSQyUwtBU70mcoDA14fQ7nFlcd/SJz8TeVJNLuRi4HnTsOHJM3maxU3JstrF9A06bTt7PsFl8NuTh2Fb7BU+SOniLXe+qufrq7zct9m8n/v835vs3BtTbvgN+XNPnNalVLjbaw0ZlNr7f8en/UqTnOo0y59ioTW3s0AWnLGjoQLc9igLd8eKPh9G53cDj5mvclZg21r12MODozVyu1HaEUAI/6CJC8i6/Xlhu/rdy+TADjIstEnqDctvTvS2jvzprMG7pJgS0OCmLKFglqMhkJZoLrotTojqwwe5IT0LL9bIa4JQdoQAkOeETwjFEcYp8Hn8uaG4CUYj5KHILpw6vl2gDRu+LhrptPi8tHuLnJ9b393K45cDShISPg6e7vgX5uNywztC3an+Tn/U184b2TW03bffzrX5tCP39jcq7JMnmC4OfNf39zt9E3KIePm/wO231/2yZp/+jrvxD8/L31Z8fk/ed5uAAMTOy3O2LtRg5OQtrbVf5BIbkJMe/ZQtRaVPqtaeyRwTY8iXDgk5BgznBEaOBwFU/CADMaEA41G3LKIQE+9lvc5wNEdgJk2q1F77mnp+Kd/Plfq38/67334YMNgjggEiOi5x9+bUQC5u8TLQ855QdE+ZjIMvpgIvPbO6kgQyGW4KRU/n6POJI/NY6qtnbtt/X2iF4DVKyG4ywcy163/zpwZ3fcvuW5NSm4efVLAapD1qbEbMY4ALlPA0b8cHZTRuxC4yvw7boS6WegcR8TQZX7AaJZcIiGwd7PA+GQ+GyMh4/o0b40GuqfVLzRar1Tb+09UOgfstInA2iZAHdFgO6Y6r2EO3sOjmiJcm2MeZPSUsf/O0iDLiGkeBZhxvyIY9xhWjDj5h87PAwYi3gU3ohpO95YFkUqxXAIjPfzbKi+L9UF3+6AoQsmxLemUXarg2JR2nDYe11y5DY5kMg/SjPb98F0fNC2b73a//G9+ANQSwcIEjnXQF0IAACTHAAAUEsBAhQAFAAICAgAuKBDROXO3ToRFgAAMxYAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX3RodW1ibmFpbC5wbmdQSwECFAAUAAgICAC4oENERczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAABVFgAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIALigQ0QSOddAXQgAAJMcAAAMAAAAAAAAAAAAAAAAALMWAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwDCAAAASh8AAAAA" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | <ggb_applet width="648" height="588" version="4.4" ggbBase64="UEsDBBQACAgIALigQ0QAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ1V4B1BTURMuIEqkCKGE3hKiKEFAioJIDZGiSEkgVCHSpApIJ1IUCCUKCohKEVBKKBI6CEgLSJUqJXSIIL1JF178/3/em3dn7rkze+45e3fv7p7v22gD/bssjHyMNDQ0LDracCPqs5l6fwdcoI61gSqmNDRcRzpwdaT/+JqV2RPOkZpf/RvP6iim36aQ1sXzBOXJbc1OnTGuN6MGzzwVUZ6G++Mzrb6pbM9lCmglAWHvtLXRTjfHiehyNvpmETH83vkXYmJhcfFsDjJtXdENHL0LTkN3BmUHJwcHd/6irAYHvYcyao+DF0/Ih0FJJSIrP4s4wtTUqkWnnx0XPdHDacGgBVny1QE7Of6/3jm2xko1iDs4Ogp+G73tt17t+yhaC9YFF5eS4nYZKU4Su/VkJhRtacnJKqTMxhmTYZeUhPBoOMw56e7u5oxiFQapnmw+f3TWVx+0b/nVHwOUuA6WU1CISU0VmEJjPt8EjpPJpKEhzkVD3cAChFwDLqmyrZQM/7jyCt3RuC0AbDg7DcIAu3xgBEQrGORIjwHGKtARcVrDOHTrthxQPNEOt4hrzBMnvg7TArPFopF4cU6+rlZwsl+02ogwVUoK5fvf63NxajBMP0IERIQBbTEYjfLycgN5sElgHiJP1/YyiUTKqqw0qdtq48+Evn8Y8rdiQuRW5DcGY+KrB8FVBWt/j/c13RYXFzXdPCaqRckYArNH7COnWAWCZENBpdNiROXyuCfzSNb4HM844fhTlc/xKblfYaDsRmBxR6BJjmzzwsKn0WrP7BVZuuysVt0LIGMY1c1NnEwxLOHLl3MfZOj/drERaFpEj3x5+FawIjfX0eyD3tvr0cIhJ/27An0FSWX0AyMjV14KqzbMeXCCXDsSFZLrEfS1p6uk8VL72NEqj4yJjPR0EBMT07YfT/Tw8HDO4sHJzg/7xfYLVyUkLHytfa4/1S8/P2Z0KBT4EjCN3RckurYqBe7miUtKJh079qYmCJp33BXGiqlGRUa2jpU5UhQUFEDLB30dMkxqyysrpKn6IM1vBd6HFCEj+W1FkJKLtXX6hKrvaspqn7NdT0+PPJQOcagZdalj7sdib9ob/k6sxvDADwoiYrcciU+9NDZd6yPxIuF6PqCEtdiypnR1tLExVEwNtihTejUFMxsvZuQlFCjx1LzMeVJeXt7L7rn7B/HkDyP2DMm1Dli1zRYfQ/kb8WvkKr1zJUVFknLLmTsSd7gjIciI4uLrBNvWbQUgO7Duu52dHVzu5s0oHE2VUOeYZgkr+KmfH1NniNgEyvly57MSzNDcVO5r/5cAv40pn92T2vEFuX9KIiN6+fEHtQVyRo7tInQehuUrzYoqBzPPE2uj7hE3qca+Wk5ETIkONyUVIAMi4hZmmp577Rk0yaZuLHS8kehl8AwHPE7CZAZdTsfumW1R3f41nPLLpya6wnuxNw/eZ/X5rdRDhTtSE0VQKPTGtaLeKF7wSbBBrHUAhYtcr6w/pfkDKKqq+tB1vFzH/cGdP4n+R79zNafXpvrUU5X8YOjz58/r3LyGysXLQfrQDjHnicEvSZxMmI5LkeLEd8tho0xIcHUO6kQ9X6OlpSW5XsfBOg9dZ/hYk/6ocY0U7skkqPKaEwRC+GRcuz2/t0YeeGmQz2VgT/wyvzpVbzHOSpB8pmnHnyHtD/wdeUWPcmfWuOKzcyLiQuEHtHZii9OXgatxzA7l6osnywVfsthp1fXEVvLhKsFZkJVb2rvPezLH3cmV932fdl/j4uIq1ZwPVgIiydr7V4viKE91g56cY0pjjnUYcnKD0z81qNNWeR2ThQutfFJG0A9e+A6s+TL/kQVxsllpQFSjp3QMRH8cv7wilGOlhkcn1CN+B7LWIN9ozP7fzK3Tow/E45KYC9mANhRIGCM78wWKUZ0dW5gnPQZ6ziWJ0aIFG9F7ttQPeffj1Z98Nju+Yut6pd0HIiJZpTSe91DwRhWVrTsJlTghQqWzsJuMJKGyj6sfBIH7WwhoWnx+MMcxjbIoH5QprMRT6hBuhssGHgXFgu1PJAmSL2c9hrEDZPP6XG9v72JlCUAJuAK/WxiX7vIpKCZoaaiMsQewtIlewA9bbP4BDxpQ1mVJ4ehn7eYOkJPdwQeZWCwtEyp7iGSklW7Y9bNnJQZpOa5tkGjaMd/+yt7WGjodvHMfoOeRyyijHHxgsH4Fo9mH3pMxCQioueU59+JeSOONn6enzxQb1VFN72k5b6uNy3uFfrw485XQgMcuMOTrTs5ODyvGDVT6WEoYmZldNZYf2tY/yeDl5WVn4CpQPVzgCBB4H+Ocy41RQwrsSQJm+cF9fxyFk5dxx/sb3Ld9V+OXpbZDFVxHRX4WW0lUuk9eu82nxM4+pQaCjcC3zn1St2m6ND6v/B8luI/zzb+Y325mMRq0qMNSHz6GaE+0dNM0nZ3v6O5mrhhkkgm9NTY2lrnXIEL3XH3PVvTipWxJJXYlkNIl9hVpQhbkWhSgU959qs6sklzm+EqMbk/9ZSy3VOffzY1lAZ6kFq12FF14PvMIVQELC4uX58BwgamWsfEbMcFOJKacwXA6cEVSkcMWYbC2q8GcnZ29fcRuqPoOM+ttWCk0BJ28MISSFxgJKdOcZPoiGQG8bVSEKiBkT+nb2lyWLrAn8Yah05ubV4EA+jlwKv+IFn8YutgWuixtQ02suWYja84rI0fvrUwLR2stOLMsc2oluNpnLpNq+q3PX/qz1yBKNw/Ys23qomvy0q2/DtOtagRUtOBjqB9euzTaLzaBJXy952N6jdnHP8vG8uFX3/vFTs9NdT02+MF5S6I8xTkaWKQMI7MZr490zEfBp0jKQCwoX47/s0ggyi0be1LEV19oo+jJWlZaunBlIjvQCs1TfCC89iS74e8eeVvgaEngpeD1/olcNorngFV+9XU2WjplTgFjhaj1zG0u4ObM5se+LeIJ6ycnNzeWO2JYu5aNpU9paWlefCzCv0Wqw/xxPFubbP0XOiIIeKW3fGNgvFGgdLtryJMn0nKB0FgAwBWFQkXX1tba+9huhTSdfxzFX5GXp51+bt+IW9DCL+0aGO6VsXzdeDIpcLY5gi1gRoF0hlMIDJrORwBSgg9mo0QrN8Yr9E4d5Epn/e6RbkUCHh1oMzS1XKCdwu5bHYpQNb/4p1mXBSen+7tJoAyr1WBXYOugJ53knpHHj4IW80Y3v/ylVOGs+XskYi+avs+oDd3WczvktE6Ato9WBiPyEUPdmicHc8KCSNxM0Mdvfi/G/hk2pbQg+JUFhhFpTEqPyw11WX+lrD13PcLsPvWlG51V8jmqNerEOj+FDMk8VakTsbr/ysTd3N9wbPMbkU/6Bjn3eGhKv/saiIoabLiYGEme/6k3F3PQVDwxJUZnrUx7dqPSpkTi6cQ6DT+9+pdNEQsw+8W3+ZCpNipCmSEgw+t8ob7nR3dHfoAxvEJ2g+c8l4Pjo6OjDWj007KrqkxPv20iZzfAs2B0khOhBGX7PoYVR3N2x/r+i5SwmE6NVUCJ6I3Cb89AxKhNkQ9COOPF5yJGde6Ttfb+KYZs0djFNL+FadHLtpGxtyKbfcyr/acZ4GqO6qRfIQzZpxyhRInGHOri9pbnroEi+mms279zM3TBGJDhotoAt9fjeHTOaS8zd5hSRFevDhieFB3tMnda/9UraHfJtlvpEYxWITv/JywvJyvLob/fqRppmsfX3wcxWebpCuxo33RVr30QTfGDtbx+FVj5kQwVBsp5FixkX/uyhOi4m6frnhSc+u6dJ8VMPZRi0nF3QtNUTyXSkekGKXzOT0byMG/l0T2iSPI0MQWjTq3gLnAYJiARsBvGIcGLTreqewDD1ERTFMG3zOJi0K1ZztTpfvRlENEoDjCbBKXio5sl1Q7v0K3shRj1zL5/M8p69DkMt5775FZawH7uj9f2oNK5uU/3GqTWMxdxNiblyehoW0mkT2y7rJ8ref2VPq4p6xzG5kGy1LooKluuqfQNQEQ9RL2ymnxTrNbPwUDeSyNFaIY52QpOc/GCyo8kscaf3262c+/HXwU9DrdnAK6/iut6N6P/IAQHwAbtHc5RoU+Ws91jC8vlk/qAIE16A34URFeX6lWai5F6Z8Rw+tHIsksHc6fSJPD9kjloc0+ZY+sTncZ4+tFAlZ490h0xoPYLnFho7FAcvRgdaZ/QH+z4ttrEAphAj8Q7NR6No9PdFaE5Hx5oQWnx9gwR68aOJYXstif+SdX945ho+oanGctQYcNpwBed+xeAVNTEnMwFZhYYk3KvTCPeo3M9x3uM9WRl0VPJGrCytc1UXvftuIuK6ce/fuX/4asFVNjR0dFK4jDP2j2rKu2aM8d+cU9M1Bvvub2+TyetfquqtSpXwgPeYep+l69ODK69bS3qUpeZnryyvxW9Mdq+cVPKt5PlmLtq9WnRAmQ9swAqfFtJaYFJeojf+hbkwA/h/8TH3LJ3SgxUGy7TQ9/wAbgr5VBx9hhyMIhQmzIYOX01f5nWGLbUoRPwpV/D0YCZK6QS5iGejremejBa/8W7nDeG5+xNbrYBBdgRyWlNRvCUk1LEvXTXkgj6OFiZd44YMFJvBxMDjAcg8a/Bfg9YcB7vowTHrlmfGsgJO7O7UbIr3X2EOQ3ks2hdpH5OcpyrLARrutq8c1yaUTDcMv/Mo3rb9dikRkXtkeKwpZ11eym13CV2tNZ0pXmZQZU1uVycBUU1hjO2sVt1aFKzJtoXSGs4398JmeskZsVf3+AEOp+mbsQuag1/jyIYPlAvPjhqjrBHFBnDPzq38jZ5yzZjznCWpsojngERflGydG4vykuA7pI9NH/v7ukF0Vz0cgeGKdChID/yENoZDSYhsKHfqGRxVDbnZQ0lvUK42i9xI6j7wzpO+U0KVdW01C6p3tFuTBNNZKNlWgnakWV+82vInPYmbpMUGXIwF5AAuKpND8tNVbZNl4KDDeS3K5zpUXlSqrK/KInUWIIdt6HTH7uBIJ8Pk3+y9qFzjoferg9mZmdI7jBqkZdU/tACeQwsrL2fzmi/TNlYitNhacYEXRjK4zvUkOfzONBg5hKOccHToCC9gKuqENjeJVxDi5mEV8QtiDSp2Rsdi9cTXBuyuUe21JR2/kAw9YbPpxt55rjKZRblOzmRiEXfVO7yhxES6tFbyOSf3F080C6WtwvRhJFt19+pWHyaxEu3Yx9q7kjA+/RU9vb2Yo6Ojj6xiXK19nLv4IcTJd0+G2HzA+o7E3qXxYDBHHelrx3iGP0YWIUS2yevH+Z1qtQabhv+BbnwqrPZPjuorQ76E+kvJy9195iBo2rhsp74dcEWDyeIaYwktncPL+kStBP8tTqxDNWdrnoF0iTLrSQGlH7Pmr4ONDVnWDh10vvG477Mgt9+nltLyUE8O8kZp8LA2y5k0/LJ7QLZSLdHil8MyaVnt2fMO9prahT99FTWqbj52YO2uHjGq6CtboAfIpdyZTnuktCYVBvLHJ1vD4DwplYGcnCD1MwEFf5byHe/KhUE4YrIgYLy+aCG8lnEVWUgG89KZ9frx+wJE+m+wLC2G5O5xTZm0OYqjrLSBvEhkexyhlwcDXZKEtyHfd9GKy8BT1GZFH+zgAx8YRjfdRXcWO0TC2DOo7KiEA5K/w+TPHXEY1YknvoH3RFqBoVSUi270OBUIDU1xxGhgtJGvui4ERO4pYQaf5hCuBQKMsQpKCkVz0WZs4JpDuMICfNzSPvfEVJf4b89poBXZCVaxwZELST0Ng56zNqAPHf9B8IyXpA4rjTb7FZ1qeqElZTaXmjUJc7OhYo/5Dj+PhmS1VXR6/yCMhpXIhrvhYVAcTamPJOMQOS4ZvmNGE0orYy5IY9R2FzH2k0qJyCUUV1DPcTYEy2oQ+qYh3Fug+WN8B0SXDNJMtay7VRxgQ8YVyKww1dv+m+3ojh7Cbi0OUR6cFxsnobj4c9Rcz7S91AfQtkANbTlLoPzuJ0/WvcNL7MrnutOd/P5hIhP0BvM79Xdz2fFhSp7VuGkyc/UG2xY6XGUz+QtNtoVxglwODD5EfyJzEcH0+mPzrt2u8Jfvli+p40hJR0tV4PajamVfqF6lAsxEh1KkjZtEGdPG/ugFdLUEL/frjv+3Aou/f/saCxVtEC84sBiloc8gcyr7PUBvJg9S3LMpTvk/jU+YMnJgPx+Pm2yt4KGdecflgfss/o+VffMDMhIalhtEF2rJKRiZrtDl6YTRDsfHn3II1td4WMqTnEfZjgGn7pXYrfnFAkIJH41iTRuo4ESYduKKNgx/8uNqRZjI3BaHR8RE/VMnyzX3SNqq4PhekGhDSHZFWbLJ/72A9qP0zPb2xmBhZ/ujA7np2CaOGNTcKE3xGe7BK+8NO2q0rrAusZuVUOGHR4VsTXFTLmbRn3Gzwjy2wYHW/5jITAYDH4l3HqzSxJsU/5tckyyOMM1vuHvTGZa1saTXwPMfZxl6i4RAJMBodXlEipT1o/RCgr6iv72rN7/5MDzKXjp/DeFv8usMiNHcZU9Iw9B2QzbcJKHXwwHb1KWp8c7p1EhtoqvnXCXDoPmP6pFn+QsZGzWlkvkkusfwd6+fRtbWAiTUVTkTQMQZrjp4bhFyoisZC7J7tHkaxkLybblTgq/SNDO3kmQlulfmd8DhZYWHN70P4t7+aRMlNNiEuw9EMnqMWNjZkRGQSHCq7G9ZiYp3NuzFZatkcWfLyrxP4pAwmc/zq67ScHWzk47Fjdakz8/CglZt695pbBxNnefOMu9EX0WcrqRQw46+0s86JI64xmfOj1c6Wpo/1p/XLZmSG6NtadMbNmQvK0L0L5pt4MtznZGwHvCt2/uan39UePQw7c1oCdlJpu8xVoN9fHxoQJMF7S9vb2XCW7M5RN/v6/uJ+cJfUxmN9Q9kh+NxWKzPn8mcRXaSIu7KefaYzDN/S6M7SVfPZBIpDZE2QG8hChPw5jgyRf7ic7OznDqES+BpvKsrNraca7CX78cEt68me/UtrK0XOWLNMZC/ruAPZ+v6g1aUFAQs/OrZ/vCbfz5gfN0tIOYLl+M7aeunh6f1drExp1Sz3mEqXTqKr/n+aHUwHj9tBE9tP71m8ztXu/pn7FPJ3tnGhi9B/w+afbEQFljk9ap4IyA4Iy5Gx3PuGEAST4r0f7XmiMAIzQeUQHb9nXg0hHE5EbJwbL4f8RE3D/a1ZqFpwJrQ3kwlcjr0zNCeZu/3yDi/v++Xe7/+nZcYI1PtRrMecCuDXRBYGBg6+hoymMr0cRedH2gj5N5eFNWHEjgnN4WK0Y44yBd2yLY1M1wxahCS+fJMMhnux/EJdpM/teLMz86aPUbBq0hLRLPV40rJO/wVWhh79cX1foKtFTkVd6K/Iba1/Fw+ZOuf/9+zXahSGPM0H/bdgnrV9czjX84c12aEY5BmuJk6YjBqpClh93Of/sQIibjo4BdPmCsNYQVGKahEyldeg+GSQC0gkEoCGNEG9UsymMqwb5baGcT8BKgX6eY8D+A+xkMTBFS+69YO5TqiYm2I+5ag93uzK09HA310tHShxdr2IT/H1BLBwjlzt06ERYAADMWAABQSwMEFAAICAgAuKBDRAAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAgIALigQ0QAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vl5bxs3Fv87/RTELFAkW1viNYccKUVToNgAThPUyW6xm90FNUNJrOfqDMeW0/S795GcS5Lt+Ai2wNqWOJx5fPf78XE8/3abpehCVrUq8oVHJthDMo+LROXrhdfo1XHkffviq/laFmu5rARaFVUm9MLjE+4N62A2IdgsVsnCi0O6EqvEP+aSUfgi8lgsmX/MuKBUzPxlglceQttaneTFjyKTdSlieRZvZCZOi1hoy3OjdXkynV5eXk466ZOiWk/X6+VkWyceAs3zeuG1FyfAbmfRJbPkFGMy/fn1qWN/rPJaizyWHjJWNerFV0/mlypPikt0qRK9WXgBjzy0kWq9ATNDHyZTQ1SCraWMtbqQNSwdTa3NOis9SyZy8/yJu0Jpb46HEnWhElktPDzxKQkwn7GIhvbCQ0WlZK5bWtLKnHbc5hdKXjq25spK5HgWQghUrZapXHgrkdZglcpXFXgUFKoamNb6KpVLUXXzQR9yBL9AoD5KwwtC59wAT0KKj2hAjyKCj3wfO2XGkj2kiyK1bDHyZ+jTJ0QxxejIDMQNFIYgcI+wu4eZG6gbuBt8R8Pdcu5IuaPhjoazWwxt54Ol7Y0dUztD2Y6hGB+ZTwAf64E9O6ORncQY8QkRo70dGDJ6E6u/GXg7Ddw0tAPBbiDtw8h8WX8Fj7SIPcgiMpLqEuJmoQcJ00kMWHh3ifRRdg5WsuhQJvVvsPKRzu2EEn/kWpBl/+znQCS7l503uvYeEgP+mOJ/gMAQ75R9V/NuJO14mxu+mFLzaQeH81YhVG8MbZvSWma1UZHNLDghgnwo3iAELPERmcEQmiKmiPiI+zAlEQrMGCJm6pYjhiJk6AhDFoL8CL64rekA+cDL3AxdcSPGkc8QscDFEXgBWfADn1AGFL6PfFhkpBMjlgWIBzBhEeKgoIG90EALg3UwB+EUMYKYWUtCRAMUUBQa6CTcIGoQGd2BKUUBRoFZCtgJuOkwE1ZEiBlroArKola9czcyLfuoWD+qvGx067v2fpwlnR91sUeeFPH5yz1nS1Hr7hqIYMsaNka3he3sm0/mqVjKFLqLM5MHCF2I1JS55b8qco26HODu3roS5UbF9ZnUGlbV6BdxIU6FltsfgLruFLS0cZHXb6tCf1+kTZbXCMVFijvl4JqMrulgcZGy0QM+fuCPHgSj6/BauQU8QU0tQX5R1R25SJJXhmLAAXDfmzy9ellJcV4WateM+dR2JXPZxKlKlMj/DrlupBi/oL5JMRjcNSmBH3SKFFVydlVDAaDtP2VVGGCaMAI/LKSM+7MI8uDKPfEpmwRs+PVBs1iYwuWcTIIwYtSPQj7zQdLV9U+CqI2SvOjjI7ayN31dqWR8/ap+WaRJ7whr+/ei1E1l201A+8pY9F2+TqXND7t/QOMWny+L7ZlLDOZ4vbsqYYad/OXa+hwBqlAfDFm349KNlsYo1lNhS4MtBe4yTSX9czKjlsKOSzdaKkhdp1prKOusJLgTo2qLl9jbKRSb9wtv66EmV/rUzaDIVHzemkrcgh+bbCn79NnlSa7leXV/nvPpXn7Nz2WVy7RNZwhlUzS1q85RpkNyvxV6812e/CTXgCtvhYF2Dawd6aByImOVwUJ3vwuBCex7UNXdTeS6kp2Jqe3wnWvtUzzO6YPbltUPVZG9yi/eQdbsqTqfdvbM67hSpclNtIS95lwO+ZeoWsBOlYzXmUoFK2KDmuBIbZwINdzoTVHZJh6gB0ZToNuykrU5/7g4IGADeLg1oPl0+wwt0FNo9NFf0fY/T+mzZ5a7TGUGbT7SNnlXTW7l9IFc2SOECRgqlr8AaA7dSUswhAII+mz1yU46I5GWG2HOGa2zUnElqx33WX6vi2TfqRAzazlASGkYmPwppXSpp9uSQyUwtBU70mcoDA14fQ7nFlcd/SJz8TeVJNLuRi4HnTsOHJM3maxU3JstrF9A06bTt7PsFl8NuTh2Fb7BU+SOniLXe+qufrq7zct9m8n/v835vs3BtTbvgN+XNPnNalVLjbaw0ZlNr7f8en/UqTnOo0y59ioTW3s0AWnLGjoQLc9igLd8eKPh9G53cDj5mvclZg21r12MODozVyu1HaEUAI/6CJC8i6/Xlhu/rdy+TADjIstEnqDctvTvS2jvzprMG7pJgS0OCmLKFglqMhkJZoLrotTojqwwe5IT0LL9bIa4JQdoQAkOeETwjFEcYp8Hn8uaG4CUYj5KHILpw6vl2gDRu+LhrptPi8tHuLnJ9b393K45cDShISPg6e7vgX5uNywztC3an+Tn/U184b2TW03bffzrX5tCP39jcq7JMnmC4OfNf39zt9E3KIePm/wO231/2yZp/+jrvxD8/L31Z8fk/ed5uAAMTOy3O2LtRg5OQtrbVf5BIbkJMe/ZQtRaVPqtaeyRwTY8iXDgk5BgznBEaOBwFU/CADMaEA41G3LKIQE+9lvc5wNEdgJk2q1F77mnp+Kd/Plfq38/67334YMNgjggEiOi5x9+bUQC5u8TLQ855QdE+ZjIMvpgIvPbO6kgQyGW4KRU/n6POJI/NY6qtnbtt/X2iF4DVKyG4ywcy163/zpwZ3fcvuW5NSm4efVLAapD1qbEbMY4ALlPA0b8cHZTRuxC4yvw7boS6WegcR8TQZX7AaJZcIiGwd7PA+GQ+GyMh4/o0b40GuqfVLzRar1Tb+09UOgfstInA2iZAHdFgO6Y6r2EO3sOjmiJcm2MeZPSUsf/O0iDLiGkeBZhxvyIY9xhWjDj5h87PAwYi3gU3ohpO95YFkUqxXAIjPfzbKi+L9UF3+6AoQsmxLemUXarg2JR2nDYe11y5DY5kMg/SjPb98F0fNC2b73a//G9+ANQSwcIEjnXQF0IAACTHAAAUEsBAhQAFAAICAgAuKBDROXO3ToRFgAAMxYAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX3RodW1ibmFpbC5wbmdQSwECFAAUAAgICAC4oENERczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAABVFgAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIALigQ0QSOddAXQgAAJMcAAAMAAAAAAAAAAAAAAAAALMWAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwDCAAAASh8AAAAA" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | ||
| + | __NOCACHE__ | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 73: | Zeile 85: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| + | |||
===2. Integralfunktion=== | ===2. Integralfunktion=== | ||
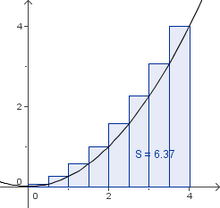
*[[Q12 Mathematik/Integralfunktion|Integralfunktion]] | *[[Q12 Mathematik/Integralfunktion|Integralfunktion]] | ||
*[[Q12 Mathematik/Integralfunktion und Flächenbilanz|Integralfunktion und Flächenbilanz zu <math>f(x)=x^2-4</math>]] | *[[Q12 Mathematik/Integralfunktion und Flächenbilanz|Integralfunktion und Flächenbilanz zu <math>f(x)=x^2-4</math>]] | ||
| + | *[[Q12 Mathematik/Lösungen Übungen|Lösungen Übungen | ||
| + | ]] | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 85: | Zeile 100: | ||
=== 3. Binomialverteilung=== | === 3. Binomialverteilung=== | ||
{{#ev:youtube |2-9wUzXKtVA|350|right}} | {{#ev:youtube |2-9wUzXKtVA|350|right}} | ||
| + | |||
#[[Media:Binomialverteilung Aufgabentypen.doc|Aufgabentypen mit Lösung]] | #[[Media:Binomialverteilung Aufgabentypen.doc|Aufgabentypen mit Lösung]] | ||
#[[Q12 Mathematik/Lösungen Modellieren mit der Binomialverteilung|Lösungen Modellieren mit der Binomialverteilung]] | #[[Q12 Mathematik/Lösungen Modellieren mit der Binomialverteilung|Lösungen Modellieren mit der Binomialverteilung]] | ||
| + | #[[Q12 Mathematik/Lösungen Abituraufgaben Binomialverteilung|Lösungen Abituraufgaben Binomialverteilung]] | ||
| + | #[[Q12 Mathematik/Videos Binomialverteilung|Videos Binomialverteilung]] | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 97: | Zeile 115: | ||
{{#ev:youtube |AtIBO-u3z10|350}} | {{#ev:youtube |AtIBO-u3z10|350}} | ||
;Übersicht, Alternativtest, Hypothesentest, einseitig, beidseitig | ;Übersicht, Alternativtest, Hypothesentest, einseitig, beidseitig | ||
| − | {{#ev:youtube |F4c0EjsDvzo|350}} | + | {{#ev:youtube |F4c0EjsDvzo|350|left}} {{#ev:youtube |k3jJrNVl49s|350|right}} |
;Einseitiger (link/rechts-seitiger) Hypothesentest, Ablesen aus Tabelle | ;Einseitiger (link/rechts-seitiger) Hypothesentest, Ablesen aus Tabelle | ||
| − | {{#ev:youtube |tfeJaIOPV_w|350}} {{#ev:youtube |UDAVccFimok|350}} | + | {{#ev:youtube |tfeJaIOPV_w|350|left}} {{#ev:youtube |UDAVccFimok|350|right}} |
| − | {{#ev:youtube |1Oba9J2cYQ0|350}} {{#ev:youtube |EkdkT6G0zKI|350}} | + | {{#ev:youtube |1Oba9J2cYQ0|350|left}} {{#ev:youtube |EkdkT6G0zKI|350|right}} |
| + | |||
| + | :[[Q12 Mathematik/Signifikanztest|Aufgaben zum Signifikanztest]] | ||
| + | |||
| + | :[https://unterrichten.zum.de/wiki/Signifikanztest_f%C3%BCr_binomialverteilte_Zufallsgr%C3%B6%C3%9Fen Lernpfad zur Klausurvorbereitung] | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 114: | Zeile 136: | ||
:[[Q12 Mathematik/LS12 Seite134_2b_3|Seite 134/2b und 3]] | :[[Q12 Mathematik/LS12 Seite134_2b_3|Seite 134/2b und 3]] | ||
:[[Q12 Mathematik/LS12 Seite135_11|Seite 135/11]] | :[[Q12 Mathematik/LS12 Seite135_11|Seite 135/11]] | ||
| + | :[[Q12 Mathematik/LS12 Seite143_6|Seite 143/6]] | ||
| + | :[[Q12 Mathematik/LS12 Seite143_9|Seite 143/9]] | ||
| + | :[[Q12 Mathematik/LS12 Seite144_15|Seite 144/15]] | ||
| + | :[[Q12 Mathematik/LS12 Seite145_19|Seite 145/19]] | ||
| + | :[[Q12 Mathematik/LS12 Seite145_21|Seite 145/21]] | ||
:[[Q12 Mathematik/Abstandsprobleme|Abstandsprobleme]] | :[[Q12 Mathematik/Abstandsprobleme|Abstandsprobleme]] | ||
| + | :[[Q12 Mathematik/Übung Abstandsprobleme|Lösungen zum Übungsblatt Abstandsprobleme]] | ||
:[[Q12 Mathematik/Mind map zur Analytischen Geometrie|Mind Map zur Analytischen Geometrie]] | :[[Q12 Mathematik/Mind map zur Analytischen Geometrie|Mind Map zur Analytischen Geometrie]] | ||
| Zeile 135: | Zeile 163: | ||
=== 6. Abitur === | === 6. Abitur === | ||
| + | ;Abituraufgaben mit Lösungen G8 | ||
| + | *[http://www.abiturloesung.de/abitur# Aufgaben mit Lösungen und Video (kostenlose Anmeldung erforderlich)] | ||
| + | *[http://www.mathelike.de/ Aufgaben + Lösung (keine Anmeldung nötig)] | ||
| + | *[https://de.serlo.org/mathe/deutschland/bayern/gymnasium/abiturpruefungen-loesung Aufgaben mit Lösungen (Serlo) bis 2015] | ||
| + | *[http://www.isb.bayern.de/download/1766/das-abitur-im-fach-mathematik-am-achtjaehrigen-gymnasium.pdf Handreichung des ISB] | ||
| + | |||
| + | ;Nützliche Seiten | ||
| + | *[http://www.poenitz-net.de/Mathematik/4.Funktionen/4.2.P.Verschiebung.pdf Verschiebung von Funktionen] | ||
| + | ;[[Q12 Mathematik/Abitur|Test Analysis]] | ||
;Hinweise aus dem Kontaktbrief des ISB [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=eceabfa3d2a86db8c7d21a432672aac4] | ;Hinweise aus dem Kontaktbrief des ISB [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=eceabfa3d2a86db8c7d21a432672aac4] | ||
"Wie schon in der Handreichung anhand von Beispielen erläutert, sind Abituraufgaben vergangener Jahre zur Vorbereitung auf die Abiturprüfung des achtjährigen Gymnasiums geeignet. Grundsätzlich können alle Aufgaben der Grundkurs-Abiturprüfungen der Jahre 2005 bis 2009 zur Vorbereitung genutzt werden. Eine Ausnahme bildet lediglich die Aufgabe 2005 I 3, die mit der zentrischen Streckung einen Inhalt voraussetzt, der nicht Teil des Lehrplans für das achtjährige Gymnasium ist. Die Kombinatorik wird in den künftigen Abituraufgaben ein deutlich geringeres Gewicht haben als bisher; nähere Erläuterungen und Beispielaufgaben dazu finden Sie in der Handreichung. Bei der Auswahl weiterer Aufgaben aus Grundkurs-Abiturprüfungen ist der Lehrplan für das achtjährige Gymnasium zugrunde zu legen. | "Wie schon in der Handreichung anhand von Beispielen erläutert, sind Abituraufgaben vergangener Jahre zur Vorbereitung auf die Abiturprüfung des achtjährigen Gymnasiums geeignet. Grundsätzlich können alle Aufgaben der Grundkurs-Abiturprüfungen der Jahre 2005 bis 2009 zur Vorbereitung genutzt werden. Eine Ausnahme bildet lediglich die Aufgabe 2005 I 3, die mit der zentrischen Streckung einen Inhalt voraussetzt, der nicht Teil des Lehrplans für das achtjährige Gymnasium ist. Die Kombinatorik wird in den künftigen Abituraufgaben ein deutlich geringeres Gewicht haben als bisher; nähere Erläuterungen und Beispielaufgaben dazu finden Sie in der Handreichung. Bei der Auswahl weiterer Aufgaben aus Grundkurs-Abiturprüfungen ist der Lehrplan für das achtjährige Gymnasium zugrunde zu legen. | ||
| Zeile 143: | Zeile 180: | ||
*Aufgaben, die auch Teil einer Grundkurs-Abiturprüfung hätten sein können (z. B. 2005 II 1 a-d; 2006 II 2; 2007 II 1 a-d; 2008 II 1, 2 a; 2008 III 1 a, b, 2; 2008 VI 1 a-c; 2009 V 2 a-d), sowie unter Berücksichtigung des eingangs beschriebenen Anforderungsniveaus der künftigen Abiturprüfung | *Aufgaben, die auch Teil einer Grundkurs-Abiturprüfung hätten sein können (z. B. 2005 II 1 a-d; 2006 II 2; 2007 II 1 a-d; 2008 II 1, 2 a; 2008 III 1 a, b, 2; 2008 VI 1 a-c; 2009 V 2 a-d), sowie unter Berücksichtigung des eingangs beschriebenen Anforderungsniveaus der künftigen Abiturprüfung | ||
*Aufgaben zu Inhalten, die bisher im Leistungskurs, nicht jedoch im Grundkurs behandelt wurden (z. B. 2006 IV 1; 2007 I 1 a-c; 2007 III 4, 5 a; 2008 IV 2; 2009 IV 3 a). | *Aufgaben zu Inhalten, die bisher im Leistungskurs, nicht jedoch im Grundkurs behandelt wurden (z. B. 2006 IV 1; 2007 I 1 a-c; 2007 III 4, 5 a; 2008 IV 2; 2009 IV 3 a). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 18. Februar 2020, 19:05 Uhr
Abi-VorvereitungFreitags 5./6. Stunde im Forum B0.03 für alle SchülerInnen der Q12. Mindmaps zur Geometrie und Analysis
HausaufgabenWas muss ich bei der HA-Verbesserung beachten? Aufgabenübersicht 1.Klausur (EIR,HET,SHE) Kurse2015/2017: M4 EIR 2014/2016: M1 GRÄ - M8 BEK 2013/2015: M1 EIR - M5 OBL |
1. Integralrechnung
|
2. Integralfunktion |
3. Binomialverteilung |
4. Hypothesentest
|
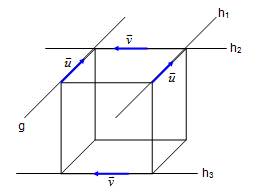
4. Geraden und Ebenen im Raum |
5. Hausaufgaben |
6. Abitur
"Wie schon in der Handreichung anhand von Beispielen erläutert, sind Abituraufgaben vergangener Jahre zur Vorbereitung auf die Abiturprüfung des achtjährigen Gymnasiums geeignet. Grundsätzlich können alle Aufgaben der Grundkurs-Abiturprüfungen der Jahre 2005 bis 2009 zur Vorbereitung genutzt werden. Eine Ausnahme bildet lediglich die Aufgabe 2005 I 3, die mit der zentrischen Streckung einen Inhalt voraussetzt, der nicht Teil des Lehrplans für das achtjährige Gymnasium ist. Die Kombinatorik wird in den künftigen Abituraufgaben ein deutlich geringeres Gewicht haben als bisher; nähere Erläuterungen und Beispielaufgaben dazu finden Sie in der Handreichung. Bei der Auswahl weiterer Aufgaben aus Grundkurs-Abiturprüfungen ist der Lehrplan für das achtjährige Gymnasium zugrunde zu legen. Der Unterschied zwischen Leistungskurs und Grundkurs lag teilweise nur im Umfang der zu behandelnden Inhalte, nicht in deren Schwierigkeitsgrad. Daher können ergänzend einzelne, mit dem Lehrplan für das achtjährige Gymnasium vereinbare Aufgaben aus Leistungskurs-Abiturprüfungen zur Vorbereitung herangezogen werden, ohne dass das Niveau des bisherigen Grundkurses zwangsläufig überschritten wird. Geeignet sind
|
- Kapitel aus dem Buch: Kapitel 2
 0,5 + f (1)
0,5 + f (1)