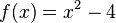Integralfunktion und Flächenbilanz: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: „<ggb_applet width="1280" height="822" version="4.4" ggbBase64="UEsDBBQACAgIACO4RkUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZy1YBzhbXx/WKmprraJIrRgRKiga…“) |
Admin (Diskussion | Beiträge) |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <math>f(x)=x^2-4</math> | |
| + | |||
| + | <ggb_applet width="1280" height="822" version="4.5" ggbBase64="UEsDBBQACAgIAPO5RkUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ0VZBVRTf/uX3GDCJsKmUqPBjVJaaoSASP2UZiNUJKRBmPRgpCiCAtItIR0iIN0iSAhKdyqNjP5f3vf3P+/O2d0523Pv2X3u5/nE9xuuq61GR3uD9tKlS3Qa6ir/AJ9dwLsMTA0cAz124i9dQg5qqGAeeo39wR7HPtSPWYL+ZBe3suLileB193S/6xkf/dODKVDPAMaiilFUxKNpKa+pU2RxSNC3UH4Eh/FD8VWTlbKMdFtkdHfqr2S2g4Qz3nTAValUqVyM1H5WnGJ5S3596Jc+0DswmCzouTrgUncThdrsrn2P33HZqTzcqNt8a5+s4C8PR9NuXNWR1YPVHpFI869/FOgXDhMhiJ17o5TnK1mvh7NeyxdQ0914a1hLGHetlPY9qtyF+JNmQ41K+WvMFAsKCoZHzf1TELW1zjNOna9Y17recOGz7IOcpuqNvyVJ6nzZ7buDz0HVJAY8/ka4nyyld7o3pEM1JOLUePqcV8xUSytqrMG3zsa1DHlP7ow0f3aOMvjInxfiQqMuLz7+0bhClsO41j3fZsf1ExIWvdl4Ll/ifrA5XTJSZLosmJ+rk5YqDbnlOCFV5bVt5fSeJ7E+AL5A2p6nNaAktJQs96U84NNJfWjuu//OM2f05Gj1Q9oL86PD5TTmEi0trTN7dNIWvjZV2q3Dn45M2nkm4OCGcuj66KPOV/hREXeXxYOow5kv7P4nel/+jtmnWhTjvox9OO5gdjI6JKsJh1qStv98mq72+jMHKlYOuay3u9x/sPFmiTmUXQZ7VeHZbvOyh/wWqhkrMnSbqU1zSC50MSfS8JqQ1DndyvH4TK4ZBfQfFiNGM1lK53sQDKKFLCS4DKkxQEdx0VyIkqGzOIQ83IPOd/UqHE6F+Jqy+DV+OcXxITu3Vq0MCwdOpbSBNBdZPygotpHk1JB/30+U8ReBCrLj1/++FCliH8un0xcc0h1BhXkMlYYZjbgOLlQ87TfQkdt/e3Ceq5X00MOjymk2zf/scKcSea01FIqAtDBSJ7uBuzKUQ3t6CIqKQNFSCbraYXyJpitB9NEJ+OkvY5jcsOkGnNKAggPnetSO4HdjD25JtMII0aVyo++idO/VvC9DUlBf7kJhe4KGf/zALwoalyPdlnq3k3e1U2SYiiTufqZHZ/xxmu+IMrj2dvFJPHap6Ob9Ld/jv4v9BJ+/v57iqK/kJptvW6oPS077zGNXxRtbjix8w0hlq0eL8eZHJcK4+pX2ktWIA9L6Gy61F4aXryabX8nqEL+MNTv0fSTv9XoH+SD3/naKAtp2pBhrvwhasp9TvuaHRDSZ15FErdrAmwDavDcbbBpcSBlD4tutEuw919+TAv//MX2drPMs9N78Yvhnsk7yljC2nnaO5+J53X6E0TUhK3qvUwuDqWjMXLPuJjRJd6ZfbiSRzwWpmHjG10IJLGEk8uvbGIKdoVecNC36ppCq446WZERAtkZ8a76Ew9pw/sUcFFk6lPK60X1sn2vKnPvnt8K0exZYPdGdhp5ITIb9zY2OTYXWEuxDnnQQLLZ8ORbtMHkFlwwjfofzIiCD9xQHczUtcVJrJY1nL6zRXcebjdMFQlpieDJBsJJ1sYjw2SciWeA67e4/6j8YRygb2Oy8ZwJBJyIlNNqGz7o9iHhprNzH8MMtkc1EcfsTfgPdBMQu8C32pOmgpqVezPx3uBqeivYvbKkt/bBjNlR7tA067tOXKrd+eZdhgqoCqKwXm3QzwtV6AYA+6z20nEIbw2idliKLhZDGpUjn3u1o5Ju7VMmZ3e2g7SzJPb/PR8iHleFhUy1ESDsCxr6wHAgi/+PYIx0h7r6iuxmRLcBpDNQSSBR9AtK9wL3uFVgPLFhhTgJZ3Vfm9PrgwdVjmXvWo8XYzG6IA4bATc/my2LEYpYq18c3WUoew4tt0ptRe3Jeyv3wRawEtrmqdUz3E2g8fcvooZGZmes/Q7maeBhatPVu2WCCcGjreaYdudnqJ42k4pkxS5x4CQpKGK2W+owyiEKBx+bOKEenQwNqZmo4+2d7gpxrX0yw7w7sImusKBcxW77FsmGR7DITbdCJzhA6ZpP2DVsAQZa1wins1YewiTgQRw3E+mtQdrsmooTg1Z0mrQCNEYcoadvJr8QEyO50cQFDORyJCPIRHVigqkYa72DUFZ11FleC0odD/LjH0DwNASSkIDUbw8SDDLH7HIJg6Ha1/ai22Gej6BGKbqXfdAJqkBZNB9IS63/78513ZHrRBuPlJNJwagRUwfyRiABu4zF3gV4I32lOPK4nmGpWEw1cOLG+CU65Lw+Ag83IlP+VjP24kiufdnJpiPgVxwrinO5fx6B52sJl2l3X2hdGV3dnLXEnOiknhJb6hBKU2OocqOcj1hK3oPjd9WoJlE0272hvdX436H8kh/G8ZpgQPyOUINi7Ppezmtq6M9heiMTtPO2D7hZcpm+A67gpKlqoWpS1GEWLgeLiahDlmXuNL1te9R4iGdcEJdkfL/W+9/vz7mKOpCzz1G5+4of3WXN3sowE8dG2I6L5DSIDG3TVXrMJoiAtFYdgj93TwwvIVF7zUrxx4wbAVJeZJXrP2UfmAX6AawnB22RL2ZP6CPwIyC2vLYuLbrU065aCPohr1b4Fzap5Mw0StnjgnCayevwXYsEdiYe5J3dSxL6WBd/9ubFhu4gpTV7Y/TNakhYPeSOrTr2DNAYI8irvffUUIcpg9j/6/BDyyLLH3QznHiW4L/UgQ7HPJGRGHEvORpCi7qznQHqfkDG2/9GPMrdlbSf8mDMpWgEka1FKPsNxY3qgmqo+9PzzYuodz2IZj7W3oA/9uk8oJKIyWrmnlqc55MHMWWqvq5+n81cBTSBzEb/alSgREvD7Z1nr+Mz+/DluLYIC9TK2TLc6SDn85s2bw9EcyvWLKIbGgNndg2n/xoNfPT339E1N12moOltFv9skhPYHCOe5egG8euqaXm8ajfYQn310QtrusZ68V1RIsyPP0gdhGkp1YjGzGZPz/pu3vz5auOsvvQwBsz03u7LX1BrF+V01Eo4vJGti8/4tuunZ/hTW07GMlA0OVQBfeUE54w8efXn99nBhScOY1XWzat8y0iVlmG2P5KTSXrtShRT9ch0NcPmxGiltOqahdvd+VUtMeopXOdq2lnEpxx6A+T17qeSnAxU2mB4ayQeTk4ccqex+pIyD9OzJyZRQb8jAJKuXEaGGxDE5mVPnXRjIH5ZP9zTGXUNkxQQMcV35ngHXlmmpG640EcNTo9UNfGFNalE39HfkwX+ns9hFm/VU0zdD37B9ngu6Nlsd9SCHsb1FFFTKSRnatPVl1fhHh4eHxxRGgVnScatIpD9Il0vClI1y4CZwkOYADm+KEOY+eg6/yts7F0lG+LZTusg+wkonR3wmVTNL/klOQuU24EK+hPqcn/n6Db9Zvq2bMdMTNCNnyrbQzZdWuYTZuvHBmUPmbsaTV1B2htHyUmSClPBnflWI0rcCmlecqri8BH2Ia/ZsaUGBydiJ7ukPRLTPAsY55/jWrHKA17athiks2Dy/FZ9vAqNVgbFAwQrC8l/XDyEIIco5uC/bwkJ3bJ/wAl1vZlNME7GVFhVDjfXrcfhZrWDbG6/9llNKabxeCMXuAze785Eu+YYhG+XktIOLq9x0uvkVt+pFjGLnOxBZfX5+93hhkT/9VyFDtuChH/NnCVBPuGWcnnvolbegZh8sHoZQ2GLN/Xn6s+yR6RaFakCC5DLo22gcyGVb+YP9XCiqZL4nCAaIwyLG7EIcruFccT9TBRHJCrF+bNxf4cElA0PpEDLj6mfGENQ7HQihANuDD+Ptz6MKpHahw1mzUMUxFgsMJ/Fi4wO4tRCHULt95a0G3+Nq18Hd5qfN4q09YwQVpujsVc5BZb5fDCzv6msr+BPN0GFMr/hf+83nWGF0BRRbFJ1l2h5ckKVuTZg9V6FJBDyYT0k1NpIqnBgZ/WHqg4RGbVdPyGRsagjVwGx9VqbNzmUjmDvMhYi/8qqCSGbpa2aJc68uJeK3U1G9mlsdHXcb16V96X/5A9w29KM1kTEiJ/C+MM/6f2kRYDpQS+oLG9e2sCuCpEDHGGB2nrVDE0suOPBf1YQxAMJKs0H41VIvhEvckA6LlxF+1h8H6UvTUOhN8oCQh6yu73CvtigNDHw9rETC7rLhqFlUIw9fjdE4BlBhMr+LIw9dLDTm1u78HsxeZ4jmXrX6VeNzuAN3HqwnzlXMVIfg79BiW/ULmR52vmME9Nd20INGPcZ91n5L7sC9uiZ//34DCV2zHDlK2EoSpoIQpF3Mwc5gOleuC/ZUaWk3SQl9odlMWPHGXlL7FY7rRgFNVUcms+sY3ISreHaQdcruF0dc1FK2XNme1XzNvZppcSVjyscU5tv4xWbnpQmMsePzDhKGNEyeeAeaxZPJLd2nzxeEtsx22b9kkS5vtzdkU+lXWxF93vBXbcjmtwkXxn0RI2JuyNbWDq1szhg1EsqULOqDknhW7pcAimL/NaiG1Lw6RrJMghogimXBgCMzBWoB41y39HiO+OeXa/Ph7eVlTATwp+3/cq9yghj+vh3PXsmMMHSKAJECyChO5lQHFgA71rJo/9fqADPzcr2BekbuxZ6I4zGjuaJPtK798xdeEXIRRAY/LEwl9ukwgTEywLnI9De51U0+MhZNYbzuk3AmCIKOxWYS91sT/UBT/4T+qAxUPvyGx8BGivP+ngWPBgLUvAVzHYNTGn5x4+yYbQ0tIudMNGup7xMRxubLynaLCE9Bxn9wh4sI3xtzIcTIO80oSWWF8PL0oiynDDKmuFeVpGqash0wujgnuxC+RDOf6GSX7s+C1uyUX6WHRrR/2yXLeBRcqGFbZ/tgML2RwAh/XNEjuVvruX+qLx5HcEjWINPXWKtqZG4xz7WS+p2IaS7NC+gb1YD3Odn/6YW38SIvChdeRtIgh00/woNDC/YDDc7/cz7kGaZ8qrJ5IY9PA8HHo6+vT2SINlvdefxBfqPh2LEwQH03uGXWuuHPa/pOS7RG9Wmzrcr3qWu2n04xP0QYYnn93DcmpA0Kb9geP1hy8N8LlLuKsRajnVxbs9tUyfIxgk3UFVWkXYAj+uMnNnHVcmd5nIn70DO5As+nsxTLhMfh/QTTbHlwS321D4bBfagSmau9LybjvoK8AN9GjVdjeflgROhYuVaShHF/JuotFYYuTkuxFNdpLXCh5AzN7dstuWSgQiAwTOm1urs+MECr+/p+EScQ2XnTtCqoPgULgu+qqqoWHpDgBi2qJaanlbyn3gM/gp0e3vtKkN3tvT1y/zMw/IAUss/ZQuzpmSU+qvLTHxLXi+v6oBUMkxcKuDFZxwzdzg7kihCIeLfEkSrFNWFw9lr2svZYlNtWNsuc8VKo11il6KfL6myOU/W/wiJ7xRUMjM9xwAyawMBVDulgt7MTwKQAqgZkgXKvmeM4QdP6nCt0Nn7MxWdyGHcsecxXOQXSTJDBtdr6zV8VfG4+8AlrMoz1gLiF3VzTYBvxR1YiL+l67cJ6DQw5ls2oMsqDdNm8fk99s930MlDLWYUMGGiIKMbWyQiC5dL5F5uOiYD97ju8pc3etR4GRIUYfqHyQSlziuWI0GbV99LJh0pGsGDPMnQlnZg9DHBJ3Hpm6DLYG5GqtV6i4w04JY0SIu1N3ZV/f9GUB/6cek2Y9epuexCzRATTQarlolnNVsZ/hgaJ+wPInP//5v6yDzDU1J1MePqP6yVAVFasld1QsB3krrJoJhjgYRFhVP8Ofsfrs9Nj7+lHEZMU0Cf8Qn4WDRdzrtUYpG3YH1TjZ1456rKIAQOkuYO8IM1f4nxXhee2Ys6p/diyjQTB5dPVd+0lzBa0Zz7ukpE1s8VWosE2nIQnrTmxDgDZQ4GbZnE03flGTNIss0r2DvEgxDq2tncb51qPzEHCoDG3ix38P0EQu+KsbnFxVM1CSoZ7lw8Ii5kXiw/hs1YpYTvOYia3/8w/n+Vce2KamGOJKfUhf63KHEnVzSzkSisVRcNzI5eLgrDC+TnP8DD3CcYGGkaHGJBi6eZNlM2Cc6vPzQx0BuaEH4+YOuHtvY0oHtCowbAzb4TJ+VjfVVpScq/JBVFXXa2abWlRVCzvetrsAIfJogFnHidSLYL8+BrVG0kh4GCJC7YCLDczi2HwIwHG0G96QoAxj5UpfYCnPUuTcDDJExFeAiLe2kmAU9mzX7c2xVsic79zk9OBd2tJmF26Vuip5/fVxAsarW0FUh2lZ/MzSxxCWOvgd2JsOMLFq9ufQqHX9CU82N4HXTX33WG0OOWglSOC8S+sP+/gJTbq7SrCwSwbriK8d1u6zcXCdlZpvsphfMQ/qtVmT1H5Wu0WHYktRoScYT8Vj7jKLOTQ+u1GGtUndV/Y20jk7W9VlWfpoRmRHgpnmWD1Ye8lcqsWokUW/X8YSsUlKTHx5PyNWpPxssbAtw9UzTuRcWEXXMVNiAy9tymfwXe5dbC9Nf/pSGw5EmY21fg1GDIVuq2nAig5DZ2aINMRzbiYB2MtuHlNayWmHNnVvyXEy2sG5hPg/5ceErGhGatknsOtg6o0XXl6WfW009mC6gneLYOwbu2BhevVyPY4ECbM8PWxsHF5m/0LGA+0RQ2w/Xo7SBtHBGOdGpNorSL1tvIOkqo3KI/hGsx1Ug96p9ZjPde6L/l6DyGY1aJ8Fe3uqyse8PL3q8wdDJLSaDzJYkLvtRICD06WTcqGEnKYz7WN+wE4IsyGsRxQq6D2DAhVc5Uvgzz4XQ1odmf3v7mmr+bhlCOBI0ZV2yVjFwmTOq3gnbAv/nz3olMnM5m5ESYv77YTqz/sHHCjw7rPv7twrPDXIS4mVNSsxzjBovLgzk3s3sgNBb9689KEQqpZno3MKM0mQnrdJwBIo9Ui6SjGUCDYAhD4RMR7eCkrB61N1n06uDEr9cCo4ml/atHKmqWWryf7VOjMpN/xn0BLnE8aqhciJeFWZPa5nEnB3c9SfhNQBX6/7z4AKpkV7rtrnZR+C52pFhG+EOcEycvCDv1x9JLbnPTCh04zofjIdoIFjep1NwAVTlH3ELMGc8rFcMqR1j3p0y/SbkuVpWIXKwPd1+PXcp/VMMpFKMdX4orlwa/vf3YuY8lG117IHiBbwSa6kwx2aenv57+334LAbxpCrO6E6naq5ss5SXFcKIV2zdaVlocNc2RRyojpqLx/hODZZWUDiQP/AW62UW2iGX7xnV9qK3F9zcqmhXiOMfV6k9OfU6jh4VHlcjWOxnBzi39StTzcVMy3zMu4FoK4MaE/nT1fbFSmVIT7MuafommOZhGyO355Jv+HuxeA98Eyk6qecXSpyIK47iQzHIFVm/lk0dTsyfoO7t7ve7RHQ4TktDGrAr6WTYiS0t/h+ebUH1utcfaju+2BPOGRIDaoo9FE3UYtCj45NmayrxN/nmJyGurX0ZioJ/ex1DjI6cFpnaeQVAml5PUJ1jvP8/QLDfIlQFA293vJqB4mRjJNWkQDmQSS2M4q427zrFbu7PSTndO3oY5Gh359E8tH3lOZBsIldKoIHtEXoo/ggO9TaH3FIp0pZFYD+x3UFI6ttHnDRK8xpFlne7Eq9zSgrmF8WOZtHId7aVR+e97UlTdQsdiKyauCrdFeYlND88r1oIa/bzAFBZn+EI68JHntomSRYX6kJO4UtT/h1m9su3OsKvU+bbCQfe4qUQcj+/xUHtMoKMbvI8Z87hXQSim5/X4qaLrT03XNeWhTU4S5keS7esKZEGVOOXr4ZB+ztr7+RQHtZN2bYEnk+tyRYkafdOtJRKNpP+VoP/+o5QnH4Gw9VyZ90POlokB3qXtM96ejRL1/YtdWQzcMhV+xpsedWlpAOLxK1hrlmkVp1KeFWKPcFumRk8Ix4SRMzdbPjdAZCbLy7YSQ1YMMy2MHW0Wv+6x74f4vApRDk0i907cnJQHNEW5+djLnnGJOWbEdOSPTSC4IzlSqVe4GNfTCryv+HMq5jlWQVfhJDVfZlM/0VFl41Jsgupab5Ehb+TK3zOKhk8e8gnlO3KvVD0v0jYXvkAmUjxevcv1IkZy2Ga623DBUaOOjTSN4/T7yJfiZoqkc8Kxbr0FSz07Et69vzkqWb0OcmRvVLz07KacBN5udkJstG1owoiBcK9GaQ4pYg4csJlYYxWcNIatOZo3ThR1ZaspDM5Pajx97U5rAELLmNS/6kJeFxJLyq/JeFZbEdoNET7/UuSdun876egenCm/mJojLQxztjZj3Elzf1c2Xqppq3PIAl73jTZPFD5psvNp0flfnJsXpcOK2kmCJ2uStBdGzbPXW4Ka0QA6JJ1dURO1QRwUOu7z57a/pDL3j7u8HkxuS2J360xaw64jT7sYNHIlPPNNYkUAKVBZ0ae+uX/FiILKLmZt+rotkVxk12Ng48tVJk/+D9uSrgVijPEElzxY3cr2ff+tui5SqX2gMNN94dYo0jnM/IpubsXrPFCJkztdKeJaAzfc7LjSXEewKcfEs/ObPkp077RZkIuNAONqIpd6PXwqdmSOmDfPdmXqIOD/KOmq0vjsvXqyQLDf/xf9oWKPKftJ+bf5bCZZw/sctYN7/5P3G9bTzx+M5XfeHRsTXsvaFDw3LyAVMYDamowELnYE8xMgnMTglNjjiK/qUOx9pZmJ1esR+hvtjV01vpmihsXK+/2hjjzJ72t+siP6jr55DqlfjixLrkIPvG4UpOX8NdAzrrKP0TXnp9EAGfXr7EL7C069PC798tc7L8kDVK8hONHGRPtStDR/rx3NK8k39yn5Vb/yH5menk5Mue1Hh/pboFpu82qjS+d2cl0l4CAEcxyZAE2lv94w14eAwKeDk8DNfYryejrFgV24nyGtrfOwsq8D/TLTK+69X1eYivsBl/qbO+DwUKh986Zz9RVaHd9Pml33e/eWcfi9yJS/K6cM9Gx11EW32yZIGL6ckPsqnOv4/Tt4byp3cThMvmL8zildSB9rx5BkGtt1sPOeyuqZWSaxCksZlPGN+EGac+laOh5Ntde4mCtOzi7PK3kysVxcMm9KQQ6NRNV0mu1EimBpuJOzVc0PzgZt6XebTo6eegmx/RQ5e4ppyupb/aaerRL4gCKHRAmZDbJv87rOtznyy4HhT2IJy6XDmaJiJC9lhSV3dkwhDQpKs45Jg1/6o+fTNWcQ7IYVO3dBVcYyZYsFNtWoYzBETJ3vroaCXnWv2oVW+TSHZVa1UPQjDWxAmidE0OXlZ+r5hW7IDHla/3BMEq9eMFyqSD/3diIK2rM7JvNiz8fj9U9RfXhZKaK6r44K27LLLQsvdpthPT9TO+0Y/RSzWkQJ9WiHC9TPvpFUW/13YoHDH4mGjm5GHQL69sE942FZPHEh0ssJemxfXNstzTqe0jLmH0bRgRuvbrIl84Q0zhank1+LOS4rQ6qcxtnYzrJ/uNjxlPFt9spHZfdsRE73du2ZyxX/8k5NOsFAVRdRc0EyJ8vg0aQC9g7GOYssb+WgitH7ouoWxKC6/uZoXe2v/M6Bsh4w2m6V66KOk/S1kld09VQhksMRe7RHH4+8++PD/7JhJz1sNReb3O7DUGoGyeHQfQlrOLTAj94t0szbWWfHaaq/Z9IGkxHThGaTNZDjRArWw6PTSag3Fu3/XCp6jE34bR081Hkv+cCY5L0hbOhFTKxkvah/UGM1ZqF1nPxrRjg24fHj6zU67HVbl2JG1lrrxqaNW2Aj2tiGMV/gWxHVtWOBpAuJ8vCXgoYwjpFvvv9sOFyYigtFzY+LXmptU2wDT0qL7fimveI2Ew2QVER+vfS0jZH/lI7Xneh7972lEJHu6LUSLejtoyR4CWNiMoR+Hs0e+egYbtP9uOjSjDNXwhgmj/66tX9hX5scY2l+NeYYlOMECFwGuVAiWRadJcnHd9I6DfNe5rGk+9fRhWtlqpoedwSG65rlROvSfLnqvF0zCiyjXHIh504jvAC+S9Xxx1G58RLBsRQn1HIBJxcVSGXoIrsIOgxm9aY9ELKsgXikIK9AwRK/RtOqPJt25wWVnudJC25dyx/DCpT120RJ8iuReGX2Lwu4dFeXn0zDCuGm8p12DlDToe3AqzPHvqYCTlTRk0ElTZKwURdZmWrOZ31UF6nFHzVSUPDyTTjaFr9jl5poJSm0StSu0AmM16oLq3xkKdWP8SFuW9pCB7JU5f5UqL2kIDTj40ZYD6/CdcYlDERWdvW+mGPdtXN3zPypAPBHQNpPdm6z12GXxBNPe6NSfGFLdXx3EiP+2x490bs936n/QTuEcIBIJ6ZESQv9AyEG3IvEw2ZdSNBJ2Ewr8UMLhlqun3SOaTl8gt9o9bky1Gx3Ruguks5VbjZ6buO6gt5ps3IVwSj12PxttE/d9iTgM3/0B+dBS99iuSbBjiG+0UgqPpMucSomfwLR7a7JeWMyV2OiV6SgzSKJYtm8/IYnNMZ1KYNg220vXIU0jyREmFMGmNaJ17qgyDhcySziSgzi+qHlfhSS20D3C6FYQr7oENSR5Ehkd0EAcnTB1/JxjEYe6XCww8XXWCLd9NfLinjUYDwoKi3sg2FOxTP7l7Cyf1M4+aRZinGwj50UXwZRtTEuqwx1wapVQsGHCQVv41ZFSXqUyIG2NHFaX8opVoHq/rgIGeK3JUWaRdhropAlKQcRc/ryn517JalAfdEFeN65lEzKregE9aKITi9/Khf89bVihn/9/aHrgdgr/t+cx3QTdpX6n87Y27rsOV4QVRgSWs/Z99mMLbytUoT6v1rNxr6Hh6j+VLm9MotOrFYhGqLlZpW/6cb6wG99vwV6hiqVK/LYjS36wer6UjEN3vWhQ941Gm8A+TgLqnPCLP04eiWw8WTT2OFz8kHj6niszqp2QjVpVh8nvfVdWtcSIlH4kRA+PpulJToXNx74b1JHCVf9OzjRS3C3QtmSWxb6BMmnhAHusy2Wz62vSyoO0pHbQn+WjcxrPfehQ9M/CmgVViMOWOzFA7Ljy1i2pW7aYS8eD222PvxGcpV79ZLtNzVz31s6O09KwIHcpmQ8ZFfUTVMJY3TxUVaydHxKyqRL7FHZwTnblXT6hyoip6RLw0lDVVilWsiD8H1BLBwhoZZ3jcyAAAAshAABQSwMEFAAICAgA87lGRQAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAgIAPO5RkUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVhtb9s2EP7c/oqDPqVAbIuiXgu7RbuhWIC+YemGYR82UBJts5ElQaQSp+jP2T/ZH9uRlGTZSbymzYoFTUiJxzvec88dT50/324KuOSNFFW5cMjUdYCXWZWLcrVwWrWcxM7zZ4/nK16teNowWFbNhqmF4099Z7cPn6Z+oDeLfOHQhKZexKOJG9Fs4oeRP0mTJZtEURYznySJ6y4dgK0UT8vqLdtwWbOMn2drvmGvq4wpo3OtVP10Nru6upr21qdVs5qtVul0K3MH8OSlXDjd5Cmq29t0RY2457pk9tub11b9RJRSsTLjDmivWvHs8aP5lSjz6gquRK7WCydxAwfWXKzW6GYSo5szLVSjrzXPlLjkEreOHo3PalM7RoyVev2RnUExuONALi5FzpuF4049z00S348CQmPikQCNVI3gpeqESWd01qubXwp+ZfXqmTGJm1RVFSnTKiFI4PNn8FzPhVM9EDt4OIShXXLtO5fawbODb4fAyvh2u29FfSvjWxmfYsiFFGnBF86SFRJRFOWywQgOz1JdF9wcqXuxQ4CcoltSfEJhtOeAhR3Pfuqe+q75tW6PfCQji6ppjxq06yN7vbU4Tr7MmvdN/tE7vfPusBePIkh0eD4D0XExAwUdEWIiowe/ewztY2QG4tqBdIux/mOYgEEPYzP5tqD1TpFg5FTgnpp/5vdm0L6/SXqv0N3JlHtYDP0jFq2BhzXou0n04CZ9Sk8J8e80Grl7RaavMHYk3XgM+wdDYj7rS+C8OxDItZbtyoLiG6mPSBNTCoFAgAkVRli5AiAJDpFOLA9IAH6AjySGUI8RUJ1LPlCIQcsRCqbgBTH+8U2ehRCgLv0ysgkH1IeAAjFl0gdEAUypRUw8ihJBAAFu0taJNktD8EN8oDH4CeDRtCqd7xQ34onRugeUANWbSQQeZq8Hka7UxO9zGTzU6kHoQqi3YqnGMm1LNO6IgWp3MPfqSooB3TUv6iEsBkhR1q3aAy/b5P1UVQfSeZVdvBzA7lY4k2oshhfV7j60F9fedfloXrCUF9hUnGsmAFyyQhdMY2FZlQqG0mnfrRpWr0Umz7lSuEvCR3bJXjPFt69QWva2jWlzi895mxUiF6z8FWmiVWiF0F/q5groL/UoIdZKVlVNfn4tkTuw/Z03FZ7JpVMSjn4cuLYrQUKmMR1+PExGmTHNeUqndPxDsDRc37EWW8v8cvCMbbns0V81Ih/Pz+TLqsgHpOtKlOoHVqu2Mf0Z3jiNdulFuSq4QdbcYdjpZBdptT23iUWtrg/XNT51+KarH6qiagAz0guw31l1Y2pHI6MPNki5RsY1EkOMRD6sk8QzEmZM7WikMOj2aJ2jpPeSuL0ZIU2tQeVjUhrG6L6pLYV63T8okV10nhIr/7bdpEi2gcAo8KOwTZ5taPetkP/Oynx2QML5BW9KXliqlRjutmql5f7A30fzVvL3TK1flPnPfIVp+57p0qnQmhU1Fm0u8kxscKN93wHMdPB/wdPbtzlfNbyTZ4Vpmy38ZtUdE//Ga6PqVVNtzsrLD8isg6POZ70/c5k1otb8hRRr+QXfcTQXkuFNkI/3ofMSvch0UULolMbVAdaqddWYzhgTG0edxdu64VJ/VNjIAKrBcrPVRelk+wQWsP3jxHsCE/CNZl7wDbbNoAy5l21pbAxhXZqeXMcPqvQjlqODsO+gxeU7uA6sqNdMd+0dSgW75s0ebkbbmyo/RBODZVzGAlNrBZpLNeeWharLR6hRoUnnESd2WaOwDF7gRwBSLxht0pOfRJ5zU+Ut+SwWN1Ap2w1vRDY4nRpQ8KRtd16v9+yhgCJfCFQnJwv9XQQbgb5M0MkN2xpnWSqrolX4ZYiMLndfhvZkXWXHfld/d+KOMDKza9wb68lSbEe8RKqJT5iE+xl1K87eMZy/Ja7jGGXVZsPKHErTJp2VCvOWFc7ugmau4T4jFltPB85GoFX9+qvi77+w2pepKFj5yZroFP8rDQ72HnBiEuzfW9T/OoqQgBqSBOQGS/zgKE3eLZeSKx1Y/T2BUQ2TYyS6fyS/NhrbG2E4+9M9jv2NwqR3fCmcWD1zYfmG0u86YfZQdWuEs2dwnkS3A+0eATrqgSbBvWpTiq08Zztc2CEPdzB8nyq+QyP0LO1IEh6DI8N2TMfGvOuJg/G+MPE+dP7gels4L7rb7SQ9BSTFSfrkSQ+l6fZse70PWrcwaPg2ImXHoTNt4b3BmxCDHb0dOm/UhUgt7nWF+5aqA59GXZzxXLe1Vk80frvrZu7Juez/xLnY4OBR76s5B+/15BCC2bgHM19N3f+pPvsHUEsHCEnWb73GBgAAAxYAAFBLAQIUABQACAgIAPO5RkVoZZ3jcyAAAAshAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAICAgA87lGRUXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAtyAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADzuUZFSdZvvcYGAAADFgAADAAAAAAAAAAAAAAAAAAVIQAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAABUoAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | ||
| + | |||
| + | __NOCACHE__ | ||
Aktuelle Version vom 11. Oktober 2016, 11:45 Uhr