Maximales Dreieck: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 1: | Zeile 1: | ||
| − | <big>Gegeben ist der Graph der Funktion f mit <math>f(x)=-\frac{1}{18}x^{3}+\frac{1}{2}x^{2}</math> | + | <big>Gegeben ist der Graph der Funktion f mit <math>f(x)=-\frac{1}{18}x^{3}+\frac{1}{2}x^{2}</math>. |
Für welchen Punkt P hat das Dreieck im ersten Quadranten den größten Flächeninhalt?</big> | Für welchen Punkt P hat das Dreieck im ersten Quadranten den größten Flächeninhalt?</big> | ||
<ggb_applet width="745" height="527" version="4.4" ggbBase64="UEsDBBQACAgIANEI50QAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZx1XeTTUXRienxljMBiyDYPB2GXNmjRjHckyluxrlqxJRSTGNGIiJhEpxVBkV5bKh4wsyTayREolytgiWxLf1B/3vs99z/O+zz33nnPPfSj2tpY8XGJcIBCIxwpv5sCKvayRDoOyZkzOuCcIxAexMsM5XZpaLlx2FJqQ6Nm2+57exrz7n/V7q0e3GmxD3+bLV9/Rsgm/E1oRUl3OCKVphzYwy2Up42esK3Wu+9r/SN5F2NSsUWj8uBwO3M1ghJAgDFpLkyOXP2xf/7ApoLbi/Wx7xeByzPZ24fPzOImo7ftD92d+Ms7oFxrb5Nw7GemkIVpKOaTAXFU9pTpy7Y+IhIQZhVJDllVSojyye1DTro1R1SRiSyxbVuhsyUTeLnoK9+a2aSrvWtmAAARvwkY4W6uijiDWufoDbvX0H+aiCGGwP+2WAmVk5B+sWImkIbX/wcevbyH/xceOXgvl2mhVA2KVt42TzxCxThThKGFg0nBZD0z3x54cmzrRcEHpL1TVCRH4F+foeGEwPZujl2Z+7XHX34JDHVZDff5YV3ja44rKGwmwf7SNEWs4LB2oH31XX9P3V+I5sf++jROh459Eh1UsYeEoqw03LH7021Dw3+KH0ODR1WnNmJxRJ9qgLZTcRSTnttV6WG78kCb4POCHBmFd2zgCOqG0J1qzizfEb2wfu5xRy7h/ed8ITF/XRBPROYShN7JTDa81nmppU7qzFELDTmNdjaEYh6zdbLlw//oE3l57y0LATxNtSpaAHKV8Ye15EMT2oKSO+jf5yOQ5hds9Com4rU1E85Ho5tBXd0NDtXaT5gfl4pd1Thv/JHNauChZMGSyF0biBqJByfa7NTs2/lhawveOC91X+XD5WGL5c4M97e4JoqxsJwjaVUmkAJr8J1W7Ut210bKjyeBuWwBLi/veMQpV1A9YGD8MxZy8vC3mdhH6qtXEHCKsD8K9tq+iTzcQStKupyOpwGdK8Y4iGoohOThk4FAxKYv1klFiyH516NebglLsr4j5sMPcxV6mZFCh9VBjgxRiGj4dBX0lQbrKo2+WFJQ/l3EmbxXAlYLbYOAvvJYoeWpVryzo3EKH9RZA2+n3ZrX5JOLb0T2b1hNK6kzePoym0jMNwSO1jWGFPzlBmHVltYHcd+A0eurijiRCKAF4+fnJOcIWG+makvnsTBsUstWuPK8utuQpOvmEAxHgKHTDdUcYMUoolsM1DfFblS86REUmX8L+kEan9xHLi++hOg1OcfLCOK3uEI4Ess6vp8T3cOYqKPnxbzo3U/ep9GHi9J1VEK4UIjJE1FcgTz+Is/iTxh/Dn2fWuASGOLdyzZsmgPGK95hQcakDy4CfV9hhxugjYxroQdgVJC200sxgqXgytA2E2ZBWmk/dYUOQJ2+uRt36JCud9MgdjVNEp12UJdGJvY7lD0zXUoI4m7603G8lFpk41cNSyoAOR9GoZ7572Y9NzvMIXvN4+kdB+VTenBu2rhzhHsvws3hkEuPV8b1MHysorviNlXYskR1eJg1xDV8Bw+JNBZ+otELxoaHGchm2JV52cswWfFAQ9bZqSElDgy1zYaGEyayl719BDwttXbF6ncf0EuQNcGi4PZSI1ZCHShtBzdIEulfkbVTKSq0md7e5hRuYqx7NH2kDd49unnYHmZub8zU2HivKVXmvpLct+aH94Liy+mpxd7e34eVTmg/YwywYyLAC6oPrDhzmKPVaQGs/V2+B4/gex/KU80YvLYIRSz12OfJtU4RFWuuTdZUCw0a3AzFi+NQGe2DwzEpzwu+N4+/rZcs/pkh/rfT1NoOj67KEJrVaIfj4bjFlb6O8Ld0rT6kmR2EQRFFOzl1DVRsbn0Xi9LNzDz7GL77Yj21tvbLBsIwdbdEPmAAo6iBc+kOZxgNvANPyVX9Mfi+Dq8Y5BdBybWxs3Q2rM5E/1VvFhiKaWRVbWNcDaH/QAlOrO1sL3aRYuYaaO/BD5Qp/HV7YsrDGeqpj7hA2mHFYNHnlxQtRqv7FJ9WZmdVJWUy9qrHPP46g4wVlcI9fFbPuhHP7BZJKu+sSYjnY/j195r8TvyYW9wDYyfP9K+tG6O822DUZsMCtmunl0v6Ktxe2n0sxnl8/D466JIkgJwgpp0yQ9y/oe8Hxo7v/fVN76GmImxAeKmEuP/ZjMajUuJq0p2rCiCX05iYcf2Ttxu9jG0MVjk4xXxBeD36X9Xz6wY7WqLdfWIzDDgd+/7EGi2Qr/d0xkeOZmG+r5136Xj2rWDtPZY8Tf0aE8NJNhDuNzetaJFvAWErJhlsY+OLeSrPTndYBQd4ZEGkrgn0qVedzOzBJ0PeG483+NMrkZXrX0q5fbdkszxVCtQFmN93CvgC48omOqhfiIJyMxrf46kiHD8ifRoXVan7YoldmPQOqa8SisH6ctvVFLK93Cz7VQ3kzha9sj37zD//nH0LodzhUJOxt6Z4wkqPpGYI6OxH2/VZQJ397g3p6ZH/ieVf9BHaYTBHvt5GvINLtE6m8DgQhqp2HGmNfZW6XlBoytnnrW3ldWwaAVE61tmNxhD1T48ecIRA5zEJjMFTYKIb3KRkNNsncrgobSTx0Temohra1Dlb5akRD6+ell/6pQ5oOb/vyiL5mj69ydPWBIV3p+XfnTmOn2v+z9gjlggobciGO+vyZS7NR8WFjM7i0k2mERWk9dQJYAr9ryFd//Fr1mfgpyXj52RprH0OqgNuB2QDq+KkZgCSQvfGCVGeeeTLufcNrQieLUBeEEoPIiCAwPHJD0dFi1I8HxkURPCl+3EY5iIzxhnXWm2cq9yMaSJagUBSM2SAM5VEXHu9PUX2EanFuVBs7hKHKodyps9DOT5GiTBIUgMkPTicV3BfpwnoJmWdKTsFhSNlkVD5GSQphxK5hNTRLDNDLHbl5u6Iu5YaYygVYd6j7LzFEb3K23MBN7lzXxVUIOnmeyzBqk36aWzxwyfno21lS5wRRn2p9HorIKcT3ZfZBIY54toEsPUMg45KNygyYVFItp/fJAAzrBqz6KL2Q0oafBW2XUtXOmFVHymWMpbZpos8pXpC8/g3gjMgTsDXMZccPLMc46ps8cjYiqEAD0qRkNCtXUOh8mkLx6ZNQtMvqB5rXDfNH6UjwTMHMnTBxVBsHRtaUqZlUUCKiUtxtcQQ9cMDpsDXn8DbF08m7SAGyrFUtitCaapaT1FtRRSv6vjrU8ZBY1Mbs3NW+zY1snZP7ZvuOK3UVSMbcx8+pomGbXMb65oLo8toTlYfrPF/ZrKqVFPAdr5PghZIzAp6W8joPrKWnSMnUOThCWKQp1z/IwlAdn5eKZmYPa2D6LKnQXUyjrT4fLPxEsrQPP3GvWstlKDb/sDf5gmzgm+bxwuLjIklGVJVJh7t21tbHGal6n347z1kiqX4R79VCxloLBEQy0oWOHH0TiR3m2VkdF3vTlV5YsrfTczvpeFmU+vIZRZqOSNbizGqbp0lcBM/ug9ng9ks7q/BePEZpuhKKrlNgN5dfgmBK2qi8Xi2CjFXRhMzUyTA/BnAlzzXxY2/616bxkYa9wgs7hA/j4mVaotSbsJ49K9h2aJ+nRgw/QDFtAXUIZpseHo8qyoFMrnd8u5TfOi+yXJYbmLrpEv2L/0T/B5op2DEdoJjoz9uZSNpIYEE9GcgTbGxJs28tOz9UrUt8sLtyUH/e6J2VyFIqXt/Q3ZFJ0+yZmE/uWmNzQIY/vOqi7q52akk0P0TI+qwBWKAsijcotjkL1KHmf17T3Yg4GnvR/pO7+auu61xehF+80ADR4ifNdcOWRCyebfJSUUIVsYgccDDWe8OGRymp+HbcWeuUqwAS4ypOsuty5kPctS44DZSWfJMMdBOU4pXc0RUouwfwq3ZEHCrIFok4ffpkA6seU/kZNdfs0+RZFNVNCNaZ1mSHp0GKI0x8YyseLaXI8geYrmuIYUEc0RJxEePph5DRqCx5Ff8uIlwWHq2o8lMaLbri26n0XJb9q5+PVHXbJVUZVLFWdnryscyODiKccK5+WNfTZiG9J6XHjfe4ABZkeSJQrTC0ttkz5/vCy0HCNu56SZQG6zcXfaiUI4ET38uZLttpLIAdd0Klu/oIMZepEoOBWAtFyEXIL2kmmKSpXmLRZbQSqI8d9+qjuJqQXH5LzYg2dV8HztmXzx7K4WN4ngPbxx6aVa3GE5fCVXUlGNrvql4Y7E809T/xx0Jq+XC/EAM6egCPluYGyBVYZ+RGty4ZOTRwBTmX/uxDIlKq4LiIZwWVkZD7AgQL1X6Q0tIZWhUsKkf46/dNZ1mDc7cBglmJJfea6ZGJD2ljlSWGiCMQvMYO1cHxaAjjheGUd9zH6LWxSLdaOxlcSs31KDh7wPsmDzgHZJE+b+ISyyZAgmROwu6LSmM/JrVfDT0bO3yb2/xIIC43JBPMMfWyij5RQdcUpa6sGLs3VVXPQNrfEIviTry06isIOwtLELino3Wy6Rik97LSwAvHTPat3f6KnkwMlg2hMGBI8BBSQYeEFO7yagWe0AaT9hFAcEVYTZtSb1YRhn0O+gwnTPRNHKvaSIgP9uIZiGu+NpKJRPiiFON7CTfFV29CbEEkL/6+friD9Zsr1149ondh0cNnszmOgXr1XAIu5BWzn7d30FSvzeneSxAeGJzWsjchDR8WSOyoV1+MShNdkl9v3H+JK3hiVDh47/lLLFwoBiEuVg6ydHDI3q+Zm59n2rmp/6e7fRw3aPxb1SvxC2dFwrpV/L7HefzbvoWWmTt2SrPepQO1e/njB8yyI0nuMjc8jO8m1ofeX/Se2f/I9afgfmJ8fbCxXov3791qygbnofBfbm/L7FZnqPJxARyajpYcA6i8yfb8ppEqzsvk5qC+kf47PZth7m1GWbEZxXRGoi4G3hmDqJ3Rdh60CrYS2DV9x+GHdf0CWrMVTAf87hgwdeXhLPPQTJbVCQ8vYnmLjwL0Pd0CNzjszWWTFHYwnVinGjDLSPy3Nk+xkbj2F9EpgXd1NdEs6KRRG26oRAT84hx1nbe00KpnuZ4+CY8aZfXUS5GUFkddhJLnbAqNQqwD1VmO51F4aEcgS2TLVBQBJQdKk+NnL/zlxrJLQaxMoWTAz02f+fo1nGXHtJwtLac5Wbm5CL8g9X8bEQz+a7/Wm74YeaayFD3yXyB77BcPwC46InvunT8tWbYYZGVua1Zj4kv6H1BLBwidVhVwMA8AAD0PAABQSwMEFAAICAgA0QjnRAAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK4FAFBLBwjWN725GQAAABcAAABQSwMEFAAICAgA0QjnRAAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWzVWW1v2zYQ/tz+ioM+JVtsi6Ik24XdIimwrUDaFEs3DPuwgpZom40saRLt2EV//O5IyZbt2E3SF6xOHYrk8Y733N1DKh28WM4SWMiiVFk6dFjbdUCmURardDJ05nrc6jkvnj8dTGQ2kaNCwDgrZkIPHb/tO5t12Gv7Li1W8dARric9JryWiHnQ8qUbtoTfjVr9Ud+VsQxlGEQOwLJUz9LsjZjJMheRvI6mciYus0hoo3Oqdf6s07m9vW3X1ttZMelMJqP2sowdwJ2n5dCpHp6huq1Ft9yIe67LOn+9vrTqWyottUgj6QB5NVfPnz4Z3Ko0zm7hVsV6OnS6fuDAVKrJFN0M+10HOiSUo6+5jLRayBKXNrrGZz3LHSMmUpp/Yp8gWbvjQKwWKpbF0HHbHudB0HV9VN/vhUE3dCArlEx1Jcwqo51a3WCh5K3VS0/GpO/S5haqVKNEDp2xSEp0S6XjAiHFHRVz7JZ6lciRKOr+ZkPsDH9QQH2UpAtjZ3HAGdc9o28Xv0Hg2r00DTugsywxWl0I+vDpE3iu58IZNcw2HjZhaKdcO+Zy23i28W0TWBnfLvetqG9lfCvj8yN+Vv2No9XAlqe1n17TT/fMPUPHz4zzOz72Gj4ycuATMNq5aTjQnpnZOzV+1Q1tt2sa5tqGVZM9+mWwQljCnnn4Qrd47Ra/K3zhAddYw6pNisNG95Kmttj1+vcD0vsiH/nBwHmHvPtCUGuDLGgYDLAQ6J/57pnkD/LxIKQPsBj6X1L4jzDYdb+HwUGnprlBVXxQTkm2SlMtZyVRDu8b1gEGAVZm2EWSCID1selShXrAAvAD7LIehNR2gVNR+sChByTHOBhuCXr4yzcFG0KAumiwaysXuA8BB2YYyQfkITCshgzncZQIAghwEVlnZJaH4IfY4T3w+4BbI1VEHBwX4o7RugecAafFrAse0oAHXSJF5tekAB5q9SB0IaSlyIrIiJYNcUUPOLmDKZ5npVqjO5VJvg6LAVKl+VxvgRfN4vpRZzvScRbdXKzBrmakKHVTDA+jzZlnD6etI/HJIBEjmeDF4ZoyAWAhEgyWYyyMs1TDupTt2KQQ+VRF5bXUGleV8EEsxKXQcvkLSpe1bWPanNQDOY8SFSuR/olpQipIIawPbqKk+uAO3J61EmVZEV+vSswdWP4ti4w2ELT7zQ8eoys75TO/vTNTRoKS3u9vr0FbqwNTgbUsF2vPxFKWNfqTggqqwpU6r8qLLNkM5ZlK9UuR63lhLmFIgQX5dJ5OEmmgNaSK15noZpQtr21lcavr3SqXa9BHk5dZkhWAJekFeKmZVO3ItkaGdraWco2MayTWQVLxep71PSNh2pFtjRRG3W6t8pTXbjK3NqNKQySovJmVJmXocjRPlb6sO1pFNxtPSf7NfDbCbGvkREMn+1o6B52dDBvcyCKVic2jFGM5z+alTezGRualfCv09DyNf5cTrMm3gnhRo24rarZlC01GaoYL7XgFnqDA/oF7taOxnBSydjEx914LbbOebFbvDRtVvxTZ7FW6eIdZs7PVQaf2Z1BGhcopOWGERH0jN/kXq1IgzcfNdeh8iV5ExDiIpCYUHRBzPc0Kc7XFqsWWSnSZF7KktwIbB0A1yCVLYpyT5SkM4eSkxU6hQ9z8Eyz/OeGnp/AznDAc8uyId3pqrMpEzvBODNok9XieGvvrAI/NhZsiCdnoA/LQTgJsYMfpvUqosxxEkk8FXcorDBOxksUWqkbf1XhcSg1Le8NYId30GrOvs7iKBK8jgYE2cCHz5KSesjSX0uarruoUcjRnyryRT5tq0siPN/gGgEkaNBbRw28qjqWhf5sQSBhkzezh1/fjKp0tgiaCs5lIY0jNif2WOMbZHBTCHTrLc6ynCq+5rkfPraJq+V5QDFmtET9/VESarIN3/XtHZIO5ewhz9/6gm4oqKb683bMRNi+0H+1bsX0HJG+JcK1Zvzm6U4tN7I9BdvV/g+wxiBmgviJg28l6VSDNTLJUJJdYGDtZe46+s0PJK44nL9XZGmixH4j65eC+kbg/mezFYYNli+2AadLxMC94x3lB/pvaJaU9+9QsT1Sk9HHIX6V0eiEIO2iPLdpiD+mLh9DExXfN+Q1x26pm4Z2B4AdpwG97gR+GPKg+4aNzfIem354sP61Oj0fiWk5ofCcOFzYO53txGB2PQ1lpq5EefS7pG+X+TfhnA/cdKDeKoMXCtu9x12Xc883nWE34j68Jg2ZCXLeuAYzX/p3vRsqcLttX6btCpCX9WXT7snfs8E1WSGc7Ib2qQwrCq+ppK7J4IU3wxs+s2Og9s4IZNhwr8j37XAVao3Vg1+oeSyyPK18WcPvm4HqNpPGCe2aNd/xo3Uvv9+wzVHM0v+/e7ENP2PlSJUoUq70U2j8/LeV8bFr5ypT/TdL7eBCyHyIEreP88yD6+bHiI36QIrk7QK0ftGY6zVdq8xeu6v+4nv8HUEsHCAAj4h08BwAAkxsAAFBLAQIUABQACAgIANEI50SdVhVwMA8AAD0PAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAICAgA0QjnRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAdA8AAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADRCOdEACPiHTwHAACTGwAADAAAAAAAAAAAAAAAAADRDwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAAEcXAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | <ggb_applet width="745" height="527" version="4.4" ggbBase64="UEsDBBQACAgIANEI50QAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZx1XeTTUXRienxljMBiyDYPB2GXNmjRjHckyluxrlqxJRSTGNGIiJhEpxVBkV5bKh4wsyTayREolytgiWxLf1B/3vs99z/O+zz33nnPPfSj2tpY8XGJcIBCIxwpv5sCKvayRDoOyZkzOuCcIxAexMsM5XZpaLlx2FJqQ6Nm2+57exrz7n/V7q0e3GmxD3+bLV9/Rsgm/E1oRUl3OCKVphzYwy2Up42esK3Wu+9r/SN5F2NSsUWj8uBwO3M1ghJAgDFpLkyOXP2xf/7ApoLbi/Wx7xeByzPZ24fPzOImo7ftD92d+Ms7oFxrb5Nw7GemkIVpKOaTAXFU9pTpy7Y+IhIQZhVJDllVSojyye1DTro1R1SRiSyxbVuhsyUTeLnoK9+a2aSrvWtmAAARvwkY4W6uijiDWufoDbvX0H+aiCGGwP+2WAmVk5B+sWImkIbX/wcevbyH/xceOXgvl2mhVA2KVt42TzxCxThThKGFg0nBZD0z3x54cmzrRcEHpL1TVCRH4F+foeGEwPZujl2Z+7XHX34JDHVZDff5YV3ja44rKGwmwf7SNEWs4LB2oH31XX9P3V+I5sf++jROh459Eh1UsYeEoqw03LH7021Dw3+KH0ODR1WnNmJxRJ9qgLZTcRSTnttV6WG78kCb4POCHBmFd2zgCOqG0J1qzizfEb2wfu5xRy7h/ed8ITF/XRBPROYShN7JTDa81nmppU7qzFELDTmNdjaEYh6zdbLlw//oE3l57y0LATxNtSpaAHKV8Ye15EMT2oKSO+jf5yOQ5hds9Com4rU1E85Ho5tBXd0NDtXaT5gfl4pd1Thv/JHNauChZMGSyF0biBqJByfa7NTs2/lhawveOC91X+XD5WGL5c4M97e4JoqxsJwjaVUmkAJr8J1W7Ut210bKjyeBuWwBLi/veMQpV1A9YGD8MxZy8vC3mdhH6qtXEHCKsD8K9tq+iTzcQStKupyOpwGdK8Y4iGoohOThk4FAxKYv1klFiyH516NebglLsr4j5sMPcxV6mZFCh9VBjgxRiGj4dBX0lQbrKo2+WFJQ/l3EmbxXAlYLbYOAvvJYoeWpVryzo3EKH9RZA2+n3ZrX5JOLb0T2b1hNK6kzePoym0jMNwSO1jWGFPzlBmHVltYHcd+A0eurijiRCKAF4+fnJOcIWG+makvnsTBsUstWuPK8utuQpOvmEAxHgKHTDdUcYMUoolsM1DfFblS86REUmX8L+kEan9xHLi++hOg1OcfLCOK3uEI4Ess6vp8T3cOYqKPnxbzo3U/ep9GHi9J1VEK4UIjJE1FcgTz+Is/iTxh/Dn2fWuASGOLdyzZsmgPGK95hQcakDy4CfV9hhxugjYxroQdgVJC200sxgqXgytA2E2ZBWmk/dYUOQJ2+uRt36JCud9MgdjVNEp12UJdGJvY7lD0zXUoI4m7603G8lFpk41cNSyoAOR9GoZ7572Y9NzvMIXvN4+kdB+VTenBu2rhzhHsvws3hkEuPV8b1MHysorviNlXYskR1eJg1xDV8Bw+JNBZ+otELxoaHGchm2JV52cswWfFAQ9bZqSElDgy1zYaGEyayl719BDwttXbF6ncf0EuQNcGi4PZSI1ZCHShtBzdIEulfkbVTKSq0md7e5hRuYqx7NH2kDd49unnYHmZub8zU2HivKVXmvpLct+aH94Liy+mpxd7e34eVTmg/YwywYyLAC6oPrDhzmKPVaQGs/V2+B4/gex/KU80YvLYIRSz12OfJtU4RFWuuTdZUCw0a3AzFi+NQGe2DwzEpzwu+N4+/rZcs/pkh/rfT1NoOj67KEJrVaIfj4bjFlb6O8Ld0rT6kmR2EQRFFOzl1DVRsbn0Xi9LNzDz7GL77Yj21tvbLBsIwdbdEPmAAo6iBc+kOZxgNvANPyVX9Mfi+Dq8Y5BdBybWxs3Q2rM5E/1VvFhiKaWRVbWNcDaH/QAlOrO1sL3aRYuYaaO/BD5Qp/HV7YsrDGeqpj7hA2mHFYNHnlxQtRqv7FJ9WZmdVJWUy9qrHPP46g4wVlcI9fFbPuhHP7BZJKu+sSYjnY/j195r8TvyYW9wDYyfP9K+tG6O822DUZsMCtmunl0v6Ktxe2n0sxnl8/D466JIkgJwgpp0yQ9y/oe8Hxo7v/fVN76GmImxAeKmEuP/ZjMajUuJq0p2rCiCX05iYcf2Ttxu9jG0MVjk4xXxBeD36X9Xz6wY7WqLdfWIzDDgd+/7EGi2Qr/d0xkeOZmG+r5136Xj2rWDtPZY8Tf0aE8NJNhDuNzetaJFvAWErJhlsY+OLeSrPTndYBQd4ZEGkrgn0qVedzOzBJ0PeG483+NMrkZXrX0q5fbdkszxVCtQFmN93CvgC48omOqhfiIJyMxrf46kiHD8ifRoXVan7YoldmPQOqa8SisH6ctvVFLK93Cz7VQ3kzha9sj37zD//nH0LodzhUJOxt6Z4wkqPpGYI6OxH2/VZQJ397g3p6ZH/ieVf9BHaYTBHvt5GvINLtE6m8DgQhqp2HGmNfZW6XlBoytnnrW3ldWwaAVE61tmNxhD1T48ecIRA5zEJjMFTYKIb3KRkNNsncrgobSTx0Temohra1Dlb5akRD6+ell/6pQ5oOb/vyiL5mj69ydPWBIV3p+XfnTmOn2v+z9gjlggobciGO+vyZS7NR8WFjM7i0k2mERWk9dQJYAr9ryFd//Fr1mfgpyXj52RprH0OqgNuB2QDq+KkZgCSQvfGCVGeeeTLufcNrQieLUBeEEoPIiCAwPHJD0dFi1I8HxkURPCl+3EY5iIzxhnXWm2cq9yMaSJagUBSM2SAM5VEXHu9PUX2EanFuVBs7hKHKodyps9DOT5GiTBIUgMkPTicV3BfpwnoJmWdKTsFhSNlkVD5GSQphxK5hNTRLDNDLHbl5u6Iu5YaYygVYd6j7LzFEb3K23MBN7lzXxVUIOnmeyzBqk36aWzxwyfno21lS5wRRn2p9HorIKcT3ZfZBIY54toEsPUMg45KNygyYVFItp/fJAAzrBqz6KL2Q0oafBW2XUtXOmFVHymWMpbZpos8pXpC8/g3gjMgTsDXMZccPLMc46ps8cjYiqEAD0qRkNCtXUOh8mkLx6ZNQtMvqB5rXDfNH6UjwTMHMnTBxVBsHRtaUqZlUUCKiUtxtcQQ9cMDpsDXn8DbF08m7SAGyrFUtitCaapaT1FtRRSv6vjrU8ZBY1Mbs3NW+zY1snZP7ZvuOK3UVSMbcx8+pomGbXMb65oLo8toTlYfrPF/ZrKqVFPAdr5PghZIzAp6W8joPrKWnSMnUOThCWKQp1z/IwlAdn5eKZmYPa2D6LKnQXUyjrT4fLPxEsrQPP3GvWstlKDb/sDf5gmzgm+bxwuLjIklGVJVJh7t21tbHGal6n347z1kiqX4R79VCxloLBEQy0oWOHH0TiR3m2VkdF3vTlV5YsrfTczvpeFmU+vIZRZqOSNbizGqbp0lcBM/ug9ng9ks7q/BePEZpuhKKrlNgN5dfgmBK2qi8Xi2CjFXRhMzUyTA/BnAlzzXxY2/616bxkYa9wgs7hA/j4mVaotSbsJ49K9h2aJ+nRgw/QDFtAXUIZpseHo8qyoFMrnd8u5TfOi+yXJYbmLrpEv2L/0T/B5op2DEdoJjoz9uZSNpIYEE9GcgTbGxJs28tOz9UrUt8sLtyUH/e6J2VyFIqXt/Q3ZFJ0+yZmE/uWmNzQIY/vOqi7q52akk0P0TI+qwBWKAsijcotjkL1KHmf17T3Yg4GnvR/pO7+auu61xehF+80ADR4ifNdcOWRCyebfJSUUIVsYgccDDWe8OGRymp+HbcWeuUqwAS4ypOsuty5kPctS44DZSWfJMMdBOU4pXc0RUouwfwq3ZEHCrIFok4ffpkA6seU/kZNdfs0+RZFNVNCNaZ1mSHp0GKI0x8YyseLaXI8geYrmuIYUEc0RJxEePph5DRqCx5Ff8uIlwWHq2o8lMaLbri26n0XJb9q5+PVHXbJVUZVLFWdnryscyODiKccK5+WNfTZiG9J6XHjfe4ABZkeSJQrTC0ttkz5/vCy0HCNu56SZQG6zcXfaiUI4ET38uZLttpLIAdd0Klu/oIMZepEoOBWAtFyEXIL2kmmKSpXmLRZbQSqI8d9+qjuJqQXH5LzYg2dV8HztmXzx7K4WN4ngPbxx6aVa3GE5fCVXUlGNrvql4Y7E809T/xx0Jq+XC/EAM6egCPluYGyBVYZ+RGty4ZOTRwBTmX/uxDIlKq4LiIZwWVkZD7AgQL1X6Q0tIZWhUsKkf46/dNZ1mDc7cBglmJJfea6ZGJD2ljlSWGiCMQvMYO1cHxaAjjheGUd9zH6LWxSLdaOxlcSs31KDh7wPsmDzgHZJE+b+ISyyZAgmROwu6LSmM/JrVfDT0bO3yb2/xIIC43JBPMMfWyij5RQdcUpa6sGLs3VVXPQNrfEIviTry06isIOwtLELino3Wy6Rik97LSwAvHTPat3f6KnkwMlg2hMGBI8BBSQYeEFO7yagWe0AaT9hFAcEVYTZtSb1YRhn0O+gwnTPRNHKvaSIgP9uIZiGu+NpKJRPiiFON7CTfFV29CbEEkL/6+friD9Zsr1149ondh0cNnszmOgXr1XAIu5BWzn7d30FSvzeneSxAeGJzWsjchDR8WSOyoV1+MShNdkl9v3H+JK3hiVDh47/lLLFwoBiEuVg6ydHDI3q+Zm59n2rmp/6e7fRw3aPxb1SvxC2dFwrpV/L7HefzbvoWWmTt2SrPepQO1e/njB8yyI0nuMjc8jO8m1ofeX/Se2f/I9afgfmJ8fbCxXov3791qygbnofBfbm/L7FZnqPJxARyajpYcA6i8yfb8ppEqzsvk5qC+kf47PZth7m1GWbEZxXRGoi4G3hmDqJ3Rdh60CrYS2DV9x+GHdf0CWrMVTAf87hgwdeXhLPPQTJbVCQ8vYnmLjwL0Pd0CNzjszWWTFHYwnVinGjDLSPy3Nk+xkbj2F9EpgXd1NdEs6KRRG26oRAT84hx1nbe00KpnuZ4+CY8aZfXUS5GUFkddhJLnbAqNQqwD1VmO51F4aEcgS2TLVBQBJQdKk+NnL/zlxrJLQaxMoWTAz02f+fo1nGXHtJwtLac5Wbm5CL8g9X8bEQz+a7/Wm74YeaayFD3yXyB77BcPwC46InvunT8tWbYYZGVua1Zj4kv6H1BLBwidVhVwMA8AAD0PAABQSwMEFAAICAgA0QjnRAAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK4FAFBLBwjWN725GQAAABcAAABQSwMEFAAICAgA0QjnRAAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWzVWW1v2zYQ/tz+ioM+JVtsi6Ik24XdIimwrUDaFEs3DPuwgpZom40saRLt2EV//O5IyZbt2E3SF6xOHYrk8Y733N1DKh28WM4SWMiiVFk6dFjbdUCmURardDJ05nrc6jkvnj8dTGQ2kaNCwDgrZkIPHb/tO5t12Gv7Li1W8dARric9JryWiHnQ8qUbtoTfjVr9Ud+VsQxlGEQOwLJUz9LsjZjJMheRvI6mciYus0hoo3Oqdf6s07m9vW3X1ttZMelMJqP2sowdwJ2n5dCpHp6huq1Ft9yIe67LOn+9vrTqWyottUgj6QB5NVfPnz4Z3Ko0zm7hVsV6OnS6fuDAVKrJFN0M+10HOiSUo6+5jLRayBKXNrrGZz3LHSMmUpp/Yp8gWbvjQKwWKpbF0HHbHudB0HV9VN/vhUE3dCArlEx1Jcwqo51a3WCh5K3VS0/GpO/S5haqVKNEDp2xSEp0S6XjAiHFHRVz7JZ6lciRKOr+ZkPsDH9QQH2UpAtjZ3HAGdc9o28Xv0Hg2r00DTugsywxWl0I+vDpE3iu58IZNcw2HjZhaKdcO+Zy23i28W0TWBnfLvetqG9lfCvj8yN+Vv2No9XAlqe1n17TT/fMPUPHz4zzOz72Gj4ycuATMNq5aTjQnpnZOzV+1Q1tt2sa5tqGVZM9+mWwQljCnnn4Qrd47Ra/K3zhAddYw6pNisNG95Kmttj1+vcD0vsiH/nBwHmHvPtCUGuDLGgYDLAQ6J/57pnkD/LxIKQPsBj6X1L4jzDYdb+HwUGnprlBVXxQTkm2SlMtZyVRDu8b1gEGAVZm2EWSCID1selShXrAAvAD7LIehNR2gVNR+sChByTHOBhuCXr4yzcFG0KAumiwaysXuA8BB2YYyQfkITCshgzncZQIAghwEVlnZJaH4IfY4T3w+4BbI1VEHBwX4o7RugecAafFrAse0oAHXSJF5tekAB5q9SB0IaSlyIrIiJYNcUUPOLmDKZ5npVqjO5VJvg6LAVKl+VxvgRfN4vpRZzvScRbdXKzBrmakKHVTDA+jzZlnD6etI/HJIBEjmeDF4ZoyAWAhEgyWYyyMs1TDupTt2KQQ+VRF5bXUGleV8EEsxKXQcvkLSpe1bWPanNQDOY8SFSuR/olpQipIIawPbqKk+uAO3J61EmVZEV+vSswdWP4ti4w2ELT7zQ8eoys75TO/vTNTRoKS3u9vr0FbqwNTgbUsF2vPxFKWNfqTggqqwpU6r8qLLNkM5ZlK9UuR63lhLmFIgQX5dJ5OEmmgNaSK15noZpQtr21lcavr3SqXa9BHk5dZkhWAJekFeKmZVO3ItkaGdraWco2MayTWQVLxep71PSNh2pFtjRRG3W6t8pTXbjK3NqNKQySovJmVJmXocjRPlb6sO1pFNxtPSf7NfDbCbGvkREMn+1o6B52dDBvcyCKVic2jFGM5z+alTezGRualfCv09DyNf5cTrMm3gnhRo24rarZlC01GaoYL7XgFnqDA/oF7taOxnBSydjEx914LbbOebFbvDRtVvxTZ7FW6eIdZs7PVQaf2Z1BGhcopOWGERH0jN/kXq1IgzcfNdeh8iV5ExDiIpCYUHRBzPc0Kc7XFqsWWSnSZF7KktwIbB0A1yCVLYpyT5SkM4eSkxU6hQ9z8Eyz/OeGnp/AznDAc8uyId3pqrMpEzvBODNok9XieGvvrAI/NhZsiCdnoA/LQTgJsYMfpvUqosxxEkk8FXcorDBOxksUWqkbf1XhcSg1Le8NYId30GrOvs7iKBK8jgYE2cCHz5KSesjSX0uarruoUcjRnyryRT5tq0siPN/gGgEkaNBbRw28qjqWhf5sQSBhkzezh1/fjKp0tgiaCs5lIY0jNif2WOMbZHBTCHTrLc6ynCq+5rkfPraJq+V5QDFmtET9/VESarIN3/XtHZIO5ewhz9/6gm4oqKb683bMRNi+0H+1bsX0HJG+JcK1Zvzm6U4tN7I9BdvV/g+wxiBmgviJg28l6VSDNTLJUJJdYGDtZe46+s0PJK44nL9XZGmixH4j65eC+kbg/mezFYYNli+2AadLxMC94x3lB/pvaJaU9+9QsT1Sk9HHIX6V0eiEIO2iPLdpiD+mLh9DExXfN+Q1x26pm4Z2B4AdpwG97gR+GPKg+4aNzfIem354sP61Oj0fiWk5ofCcOFzYO53txGB2PQ1lpq5EefS7pG+X+TfhnA/cdKDeKoMXCtu9x12Xc883nWE34j68Jg2ZCXLeuAYzX/p3vRsqcLttX6btCpCX9WXT7snfs8E1WSGc7Ib2qQwrCq+ppK7J4IU3wxs+s2Og9s4IZNhwr8j37XAVao3Vg1+oeSyyPK18WcPvm4HqNpPGCe2aNd/xo3Uvv9+wzVHM0v+/e7ENP2PlSJUoUq70U2j8/LeV8bFr5ypT/TdL7eBCyHyIEreP88yD6+bHiI36QIrk7QK0ftGY6zVdq8xeu6v+4nv8HUEsHCAAj4h08BwAAkxsAAFBLAQIUABQACAgIANEI50SdVhVwMA8AAD0PAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAICAgA0QjnRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAdA8AAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADRCOdEACPiHTwHAACTGwAADAAAAAAAAAAAAAAAAADRDwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAAEcXAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | ||
Aktuelle Version vom 7. Juli 2014, 00:26 Uhr
Gegeben ist der Graph der Funktion f mit 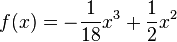 .
.
Für welchen Punkt P hat das Dreieck im ersten Quadranten den größten Flächeninhalt?

