|
|
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) |
| Zeile 54: |
Zeile 54: |
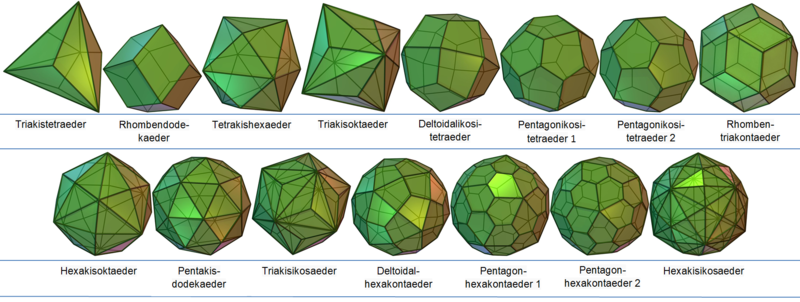
| | Bei Catalanischen Körpern wird die "Oberfläche aus kongruenten ungleichseitigen [...] Vielecken einer einzigen Flächenart gebildet"<ref name="">Paul Adam, Arnold Wyss, Platonische und Archimedische Körper; ihre Sternformen und polaren Gebilde, Stuttgart 1994, S.77</ref>, die "Ecken [werden] von ungleich vielen Kanten gebildet"<ref>Ebd., a. a. O.</ref> und die "Kanten [sind] ungleich lang" <ref>Ebd., a. a. O.</ref>. | | Bei Catalanischen Körpern wird die "Oberfläche aus kongruenten ungleichseitigen [...] Vielecken einer einzigen Flächenart gebildet"<ref name="">Paul Adam, Arnold Wyss, Platonische und Archimedische Körper; ihre Sternformen und polaren Gebilde, Stuttgart 1994, S.77</ref>, die "Ecken [werden] von ungleich vielen Kanten gebildet"<ref>Ebd., a. a. O.</ref> und die "Kanten [sind] ungleich lang" <ref>Ebd., a. a. O.</ref>. |
| | | | |
| − |
| |
| − | |style="vertical-align:top" ; width=500px|
| |
| − | <span style="color:#000000">
| |
| − | <center><popup name="Abschneiden von Ecken">
| |
| − | [[Datei:Tetraeder.png|150px]][[Datei:Tetraederstumpf-Tetraeder.png|150px]][[Datei:Tetraederstumpf waagerecht.png|107px]]
| |
| − | </popup></center>
| |
| − |
| |
| − | |style="vertical-align:top" ; width=500px|
| |
| − | <span style="color:#000000">
| |
| − | <center><popup name="Hinzufügen von Ecken">
| |
| − | [[Datei:Tetraeder.png|150px]][[Datei:Tetraederstumpf-Tetraeder.png|150px]][[Datei:Tetraederstumpf waagerecht.png|107px]]
| |
| − | </popup></center>
| |
| | | | |
| | |} | | |} |
| Zeile 263: |
Zeile 251: |
| | | | |
| | | | |
| − |
| |
| − |
| |
| − |
| |
| − | [[File:Trunc-icosa.jpg|250px]]<ref> Ikosaederstumpf </ref>
| |
| − | :<references/>
| |
| | | | |
| | <!--<center>{{#slideshare:eigenschaftendestetraeders-131005035717-phpapp01}}</center> | | <!--<center>{{#slideshare:eigenschaftendestetraeders-131005035717-phpapp01}}</center> |