Archimedische Körper: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Dodekaederstumpf)
 
(59 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
{| border="0" cellpadding="5" cellspacing="2" style="border-left: 30px solid {{{RandLinks|#FAFAFA}}}; border-top: 30px solid {{{RandOben|#FAFAFA}}}; border-bottom: 0px solid {{{RandUnten|#FAFAFA}}}; border-right: 30px solid {{{RandRechts|#FAFAFA}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}; background-color: {{{Hintergrund|#FAFAFA}}}"
+
<div style="background: #FFFFFF;">
 +
{| border="0" cellpadding="5" cellspacing="2" style="border-left: 30px solid {{{RandLinks|#FFFFFF}}}; border-top: 30px solid {{{RandOben|#FFFFFF}}}; border-bottom: 0px solid {{{RandUnten|#FFFFFF}}}; border-right: 30px solid {{{RandRechts|#FFFFFF}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}; background-color: {{{Hintergrund|#FFFFFF}}}"
 
|-  
 
|-  
 
|
 
|
−
   {|
+
<center>
 +
   {|style="background:#FFFFFF"
 
   | <imagemap>
 
   | <imagemap>
 
     Datei:Platonische Körper Briefpapier Button.png|center|220px|
 
     Datei:Platonische Körper Briefpapier Button.png|center|220px|
Zeile 18: Zeile 20:
 
       </imagemap>
 
       </imagemap>
 
     | <imagemap>
 
     | <imagemap>
−
       Datei:Durchdringungen Briefpapier Button.png|center|375px|
+
       Datei:Catalanische Körper.jpg|center|375px|
−
       rect 0 0 0 0 [[Benutzer:Thamm_Pascal/Platonische Körper/Weiterführende_Inhalte/Durchdringungen|Durchdringungen]]
+
       rect 0 0 0 0 [[Benutzer:Thamm_Pascal/Platonische Körper/Weiterführende_Inhalte/Catalanische_Körper|Catalanische Körper]]
−
       default [[Benutzer:Thamm_Pascal/Platonische Körper/Weiterführende_Inhalte/Durchdringungen|Durchdringungen]]
+
       default [[Benutzer:Thamm_Pascal/Platonische Körper/Weiterführende_Inhalte/Catalanische_Körper|Catalanische Körper]]
 
       desc none
 
       desc none
 
       </imagemap>
 
       </imagemap>
Zeile 32: Zeile 34:
 
   |}  
 
   |}  
  
−
|}<noinclude>
+
|}</center><noinclude>
  
  
−
{| border="0" cellpadding="5" cellspacing="2" style="border-left: 30px solid {{{RandLinks|#FAFAFA}}}; border-top: 0px solid {{{RandOben|#FAFAFA}}}; border-bottom: 30px solid |{{{RandUnten|#FAFAFA}}}; border-right: 30px solid {{{RandRechts|#FAFAFA}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}; background-color: {{{Hintergrund|#F0E9CA}}}"
+
{| border="0" cellpadding="5" cellspacing="2" style="border-left: 30px solid {{{RandLinks|#FFFFFF}}}; border-top: 0px solid {{{RandOben|#FFFFFF}}}; border-bottom: 30px solid |{{{RandUnten|#FFFFFF}}}; border-right: 30px solid {{{RandRechts|#FFFFFF}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}; background-color: {{{Hintergrund|#F0E9CA}}}"
 
|-
 
|-
 
|
 
|
 
<br>
 
<br>
 
<br><br>
 
<br><br>
−
<center>'''<u><font size="10"> A R C H I M E D I S C H E&nbsp;&nbsp;K Ö R P E R </font></u>'''</center>
+
<center>'''<u><font size="10"> A R C H I M E D I S C H E&nbsp;&nbsp;K Ö R P E R </font></u><font size="10">&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</font>'''</center>
 
<br><br>
 
<br><br>
  
  
 
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
−
|style="vertical-align:top" ; width=900px|
+
|style="vertical-align:top" ; width=1100px|
 
<span style="color:#000000">
 
<span style="color:#000000">
 
== Allgemeines ==
 
== Allgemeines ==
 +
Archimedische Körper können durch das Abschneiden von Ecken und das Hinzufügen von Ecken aus den platonischen Körpern abgeleitet werden.
 +
 +
Als Beispiel wird hier die Wandlung des Tetraeders zum Tetraederstumpf verbildlicht.
 +
 +
Im Folgenden wird nur noch der Endkörper und dessen Ausgangskörper angezeigt.
 +
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
 
|style="vertical-align:top" ; width=500px|
 
|style="vertical-align:top" ; width=500px|
 +
<span style="color:#000000">
 +
<center><popup name="Abschneiden von Ecken">
 +
[[Datei:Tetraeder.png|150px]][[Datei:Tetraederstumpf-Tetraeder.png|150px]][[Datei:Tetraederstumpf waagerecht.png|107px]]
 +
</popup></center>
 +
 +
|style="vertical-align:top" ; width=500px|
 +
<span style="color:#000000">
 +
<center><popup name="Hinzufügen von Ecken">
 +
[[Datei:Tetraederstumpf waagerecht.png|107px]][[Datei:Tetraederstumpf-Tetraeder.png|150px]][[Datei:Tetraeder schwarz.png|150px]]
 +
</popup></center>
 +
 +
|}
 +
 +
|style="vertical-align:top" ; width=200px|
 
<span style="color:#009900">[[File:Archimedian Solids 15.jpg|180px]]
 
<span style="color:#009900">[[File:Archimedian Solids 15.jpg|180px]]
  
 
|}
 
|}
 +
 
== Tetraederstumpf ==
 
== Tetraederstumpf ==
 +
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Tetraederstumpf waagerecht.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[Datei:Tetraeder schwarz.png|x50px]]  «»  [[Datei:Tetraederstumpf waagerecht.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Tetraederstumpf besitzt als Ausgangskörper den Tetraeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der Tetraederstumpf besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;18 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;12 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;8 Flächen
 +
 +
und besteht als 4 Dreiecken und 4 Sechsecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
 +
|}
 +
 +
|}
 +
 
== Kuboktaeder ==
 
== Kuboktaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Kuboktaeder.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]] + [[File:Uniform polyhedron-43-t2.svg|x50px]]  «»  [[Datei:Kuboktaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Kuboktaeder besitzt als Ausgangskörper den Tetraeder oder Hexaeder und Oktaeder (,welche sich beide Durchdringen).
 +
 +
Er kann durch Abstumpfung entstehen.
 +
 +
 +
Der Kuboktaeder besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;24 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;12 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;14 Flächen
 +
 +
und besteht als 8 Dreiecken und 6 Quadrate.
 +
|-
 +
|style="background:#F0E9CA"| [[Datei:Tetraeder schwarz.png|x50px]]  «»  [[Datei:Kuboktaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
 +
|}
 +
 +
|}
 +
 
== Hexaederstumpf ==
 
== Hexaederstumpf ==
 +
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Hexaederstumpf.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]]  «»  [[Datei:Hexaederstumpf.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Hexaederstumpf besitzt als Ausgangskörper den Hexaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der Hexaederstumpf besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;36 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;24 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;14 Flächen
 +
 +
und besteht als 8 Dreiecken und 6 Achtecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
 +
|}
 +
 +
|}
 +
 
== Oktaederstumpf ==
 
== Oktaederstumpf ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Oktaederstumpf.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t2.svg|x50px]]  «»  [[Datei:Oktaederstumpf.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Oktaederstumpf besitzt als Ausgangskörper den Oktaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der Oktaederstumpf besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;36 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;24 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;14 Flächen
 +
 +
und besteht als 8 Sechsecke und 6 Quadrate.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
 +
 +
|}
 +
 
== (Kleines) Rhombenkuboktaeder ==
 
== (Kleines) Rhombenkuboktaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Kleines Rhombenkuboktaeder.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t2.svg|x50px]]  «»  [[Datei:Kleines Rhombenkuboktaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der (Kleine) Rhombenkuboktaeder besitzt als Ausgangskörper den Hexaeder oder den Oktaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der (Kleine) Rhombenkuboktaeder besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;48 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;24 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;26 Flächen
 +
 +
und besteht als 8 Dreiecken und 18 Quadrate.
 +
|-
 +
|style="background:#F0E9CA"|[[File:Uniform polyhedron-43-t0.svg|x50px]]  «»  [[Datei:Hexaederstumpf.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
 +
 +
|}
 +
 +
|}
 +
 
== Großes Rhombenkuboktaeder ==
 
== Großes Rhombenkuboktaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Großes Rhombenkuboktaeder.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]]  «»  [[Datei:Großes Rhombenkuboktaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Das Große Rhombenkuboktaeder besitzt als Ausgangskörper den Hexaeder.
 +
 +
Es kann durch Große Rhombenkuboktaeder entstehen
 +
 +
 +
Das Große Rhombenkuboktaeder besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;60 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;24 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;38 Flächen
 +
 +
und besteht aus 6 Quadraten, 32 Dreiecken.
 +
|-
 +
|style="background:#F0E9CA"|[[File:Uniform polyhedron-43-t0.svg|x50px]] + [[File:Uniform polyhedron-43-t2.svg|x50px]]  «»  [[Datei:Großes Rhombenkuboktaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
 +
|}
 +
 +
|}
 +
 
== Ikosidodekaeder ==
 
== Ikosidodekaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Oktaederstumpf.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t2.svg|x50px]]  «»  [[Datei:Oktaederstumpf.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Oktaederstumpf besitzt als Ausgangskörper den Oktaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der Oktaederstumpf besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;36 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;24 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;14 Flächen
 +
 +
und besteht als 8 Sechsecke und 6 Quadrate.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
 +
 +
|}
 +
 
== Dodekaederstumpf ==
 
== Dodekaederstumpf ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Hexaederstumpf.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]]  «»  [[Datei:Hexaederstumpf.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Dodekaederstumpf besitzt als Ausgangskörper den Dodekaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der Dodekaederstumpf besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;90 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;60 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;32 Flächen
 +
 +
und besteht aus 20 Dreiecken, 12 Zehnecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
 +
|}
 +
 +
|}
 +
 
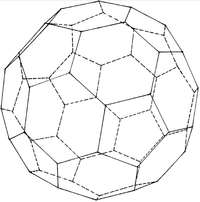
== Ikosaederstumpf ==
 
== Ikosaederstumpf ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Ikosaederstumpf.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Euclid Icosahedron 3.svg|x50px]]  «»  [[Datei:Ikosaederstumpf.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Das Ikosaederstumpf besitzt als Ausgangskörper den Ikosaeder.
 +
 +
Es kann durch Abstumpfung entstehen
 +
 +
 +
Das Ikosaederstumpf besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;90 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;60 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;32 Flächen
 +
 +
und besteht aus 20 Sechsecken und 12 Fünfecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
|}
 +
 +
|}
 +
 
== Abgeschrägtes Hexaeder ==
 
== Abgeschrägtes Hexaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Abgeschrägtes Hexaeder Variante 1.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]]  «»  [[Datei:Abgeschrägtes Hexaeder Variante 1.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Das Abgeschrägte Hexaeder  besitzt als Ausgangskörper den Hexaeder.
 +
 +
Es kann durch Abstumpfung entstehen
 +
 +
 +
Das Abgeschrägtes Hexaeder besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;72 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;48 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;16 Flächen
 +
 +
und besteht aus 12 Quadraten, 8 Sechsecken und 6 Achtecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
 +
 +
|}
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Abgeschrägtes Hexaeder Variante 2.png |200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]]  «»  [[Datei:Abgeschrägtes Hexaeder Variante 2.png |x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Das Abgeschrägte Hexaeder 2 besitzt als Ausgangskörper den Hexaeder.
 +
 +
Es kann durch Abstumpfung entstehen
 +
 +
 +
Das Abgeschrägtes Hexaeder 2 besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;72 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;48 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;16 Flächen
 +
 +
und besteht aus 12 Quadraten, 8 Sechsecken und 6 Achtecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
 +
 +
|}
 +
 
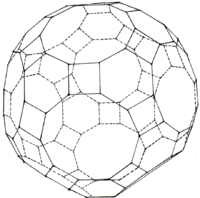
== (Kleines) Rhombenikosidodekaeder ==
 
== (Kleines) Rhombenikosidodekaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Kleines Rhombenkuboktaeder.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Dodecahedron.svg|x50px]]  «»  [[Datei:Kleines Rhombenkuboktaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der (Kleine) Rhombenikosidodekaeder besitzt als Ausgangskörper den Dodekaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der (Kleine) Rhombenikosidodekaeder besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;120 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;60 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;62 Flächen
 +
 +
und besteht aus 20 Dreiecken, 30 Quadraten und 12 Fünfecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
 +
 +
|}
 +
 
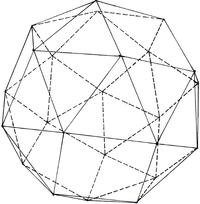
== Großes Rhombenikosidodekaeder ==
 
== Großes Rhombenikosidodekaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Großes Rhomenikosidodekaeder.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Dodecahedron.svg|x50px]]  «»  [[Datei:Großes Rhomenikosidodekaeder.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der (Kleine) Rhombenikosidodekaeder besitzt als Ausgangskörper den Dodekaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der (Kleine) Rhombenikosidodekaeder besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;180 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;120 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;62 Flächen
 +
 +
und besteht aus 30 Quadraten, 20 Sechsecken, 12 Zehnecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
|}
 +
 +
|}
 +
 
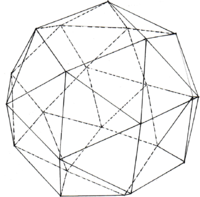
== Abgeschrägtes Dodekaeder ==
 
== Abgeschrägtes Dodekaeder ==
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Abgeschrägte Dodekaeder Variante 1.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
  
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Dodecahedron.svg|x50px]]  «»  [[Datei:Abgeschrägte Dodekaeder Variante 1.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Abgeschrägte Dodekaeder 1 besitzt als Ausgangskörper den Dodekaeder.
  
 +
Er kann durch Abstumpfung entstehen
  
  
 +
Der Abgeschrägte Dodekaeder 1 besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;150 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;60 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;92 Flächen
 +
 +
und besteht aus 80 Dreiecken, 12 Fünfecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
 +
|}
 +
 +
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 +
|style="vertical-align:top" ; width=300px|
 +
<span style="color:#000000"> [[Datei:Abgeschrägtes Dodekaeder Variante 2.png|200px]]
 +
|style="vertical-align:top" ; width=1000px|
 +
<span style="color:#000000">
 +
 +
{| class="" style="text-align:center" style="background:#F0E9CA"
 +
|style="background:#F0E9CA"| [[File:Dodecahedron.svg|x50px]]  «»  [[Datei:Abgeschrägtes Dodekaeder Variante 2.png|x50px]]
 +
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font>
 +
| rowspan="2" style="background:#F0E9CA" | Der Abgeschrägte Dodekaeder 2 besitzt als Ausgangskörper den Dodekaeder.
 +
 +
Er kann durch Abstumpfung entstehen
 +
 +
 +
Der Abgeschrägte Dodekaeder 2 besitzt
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;150 Ecken,
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;60 Kanten und
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;92 Flächen
 +
 +
und besteht aus 80 Dreiecken, 12 Fünfecken.
 +
|-
 +
|style="background:#F0E9CA"|
 +
 +
|}
  
  
  
−
File:Trunc-icosa.jpg
 
  
  
  
  
−
[[File:Trunc-icosa.jpg|250px]]<ref> Ikosaederstumpf </ref>
 
−
:<references/>
 
  
 
<!--<center>{{#slideshare:eigenschaftendestetraeders-131005035717-phpapp01}}</center>
 
<!--<center>{{#slideshare:eigenschaftendestetraeders-131005035717-phpapp01}}</center>
 
|}<noinclude>
 
|}<noinclude>
 
<!--http://www.3quarks.com/de/PlatonischeKoerper/index.html
 
<!--http://www.3quarks.com/de/PlatonischeKoerper/index.html
 +
</div>

Aktuelle Version vom 12. November 2013, 09:27 Uhr

Platonische Körper Briefpapier Button.pngPlatonische Körper
Archimedische Körper Briefpapier Button.pngArchimedische Körper
Catalanische Körper.jpgCatalanische Körper
Sternkörper Briefpapier Button.pngSternkörper





A R C H I M E D I S C H E  K Ö R P E R                            




Inhaltsverzeichnis

Allgemeines

Archimedische Körper können durch das Abschneiden von Ecken und das Hinzufügen von Ecken aus den platonischen Körpern abgeleitet werden.

Als Beispiel wird hier die Wandlung des Tetraeders zum Tetraederstumpf verbildlicht.

Im Folgenden wird nur noch der Endkörper und dessen Ausgangskörper angezeigt.

Archimedian Solids 15.jpg

Tetraederstumpf

Tetraederstumpf waagerecht.png

Tetraeder schwarz.png «» Tetraederstumpf waagerecht.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Tetraederstumpf besitzt als Ausgangskörper den Tetraeder.

Er kann durch Abstumpfung entstehen


Der Tetraederstumpf besitzt

     18 Ecken,

     12 Kanten und

     8 Flächen

und besteht als 4 Dreiecken und 4 Sechsecken.


Kuboktaeder

Kuboktaeder.png

Uniform polyhedron-43-t0.svg + Uniform polyhedron-43-t2.svg «» Kuboktaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Kuboktaeder besitzt als Ausgangskörper den Tetraeder oder Hexaeder und Oktaeder (,welche sich beide Durchdringen).

Er kann durch Abstumpfung entstehen.


Der Kuboktaeder besitzt

     24 Ecken,

     12 Kanten und

     14 Flächen

und besteht als 8 Dreiecken und 6 Quadrate.

Tetraeder schwarz.png «» Kuboktaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Hexaederstumpf

Hexaederstumpf.png

Uniform polyhedron-43-t0.svg «» Hexaederstumpf.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Hexaederstumpf besitzt als Ausgangskörper den Hexaeder.

Er kann durch Abstumpfung entstehen


Der Hexaederstumpf besitzt

     36 Ecken,

     24 Kanten und

     14 Flächen

und besteht als 8 Dreiecken und 6 Achtecken.


Oktaederstumpf

Oktaederstumpf.png

Uniform polyhedron-43-t2.svg «» Oktaederstumpf.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Oktaederstumpf besitzt als Ausgangskörper den Oktaeder.

Er kann durch Abstumpfung entstehen


Der Oktaederstumpf besitzt

     36 Ecken,

     24 Kanten und

     14 Flächen

und besteht als 8 Sechsecke und 6 Quadrate.

(Kleines) Rhombenkuboktaeder

Kleines Rhombenkuboktaeder.png

Uniform polyhedron-43-t2.svg «» Kleines Rhombenkuboktaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der (Kleine) Rhombenkuboktaeder besitzt als Ausgangskörper den Hexaeder oder den Oktaeder.

Er kann durch Abstumpfung entstehen


Der (Kleine) Rhombenkuboktaeder besitzt

     48 Ecken,

     24 Kanten und

     26 Flächen

und besteht als 8 Dreiecken und 18 Quadrate.

Uniform polyhedron-43-t0.svg «» Hexaederstumpf.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf


Großes Rhombenkuboktaeder

Großes Rhombenkuboktaeder.png

Uniform polyhedron-43-t0.svg «» Großes Rhombenkuboktaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Das Große Rhombenkuboktaeder besitzt als Ausgangskörper den Hexaeder.

Es kann durch Große Rhombenkuboktaeder entstehen


Das Große Rhombenkuboktaeder besitzt

     60 Ecken,

     24 Kanten und

     38 Flächen

und besteht aus 6 Quadraten, 32 Dreiecken.

Uniform polyhedron-43-t0.svg + Uniform polyhedron-43-t2.svg «» Großes Rhombenkuboktaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Ikosidodekaeder

Oktaederstumpf.png

Uniform polyhedron-43-t2.svg «» Oktaederstumpf.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Oktaederstumpf besitzt als Ausgangskörper den Oktaeder.

Er kann durch Abstumpfung entstehen


Der Oktaederstumpf besitzt

     36 Ecken,

     24 Kanten und

     14 Flächen

und besteht als 8 Sechsecke und 6 Quadrate.

Dodekaederstumpf

Hexaederstumpf.png

Uniform polyhedron-43-t0.svg «» Hexaederstumpf.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Dodekaederstumpf besitzt als Ausgangskörper den Dodekaeder.

Er kann durch Abstumpfung entstehen


Der Dodekaederstumpf besitzt

     90 Ecken,

     60 Kanten und

     32 Flächen

und besteht aus 20 Dreiecken, 12 Zehnecken.


Ikosaederstumpf

Ikosaederstumpf.png

Euclid Icosahedron 3.svg «» Ikosaederstumpf.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Das Ikosaederstumpf besitzt als Ausgangskörper den Ikosaeder.

Es kann durch Abstumpfung entstehen


Das Ikosaederstumpf besitzt

     90 Ecken,

     60 Kanten und

     32 Flächen

und besteht aus 20 Sechsecken und 12 Fünfecken.

Abgeschrägtes Hexaeder

Abgeschrägtes Hexaeder Variante 1.png

Uniform polyhedron-43-t0.svg «» Abgeschrägtes Hexaeder Variante 1.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Das Abgeschrägte Hexaeder besitzt als Ausgangskörper den Hexaeder.

Es kann durch Abstumpfung entstehen


Das Abgeschrägtes Hexaeder besitzt

     72 Ecken,

     48 Kanten und

     16 Flächen

und besteht aus 12 Quadraten, 8 Sechsecken und 6 Achtecken.

Abgeschrägtes Hexaeder Variante 2.png

Uniform polyhedron-43-t0.svg «» Abgeschrägtes Hexaeder Variante 2.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Das Abgeschrägte Hexaeder 2 besitzt als Ausgangskörper den Hexaeder.

Es kann durch Abstumpfung entstehen


Das Abgeschrägtes Hexaeder 2 besitzt

     72 Ecken,

     48 Kanten und

     16 Flächen

und besteht aus 12 Quadraten, 8 Sechsecken und 6 Achtecken.

(Kleines) Rhombenikosidodekaeder

Kleines Rhombenkuboktaeder.png

Dodecahedron.svg «» Kleines Rhombenkuboktaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der (Kleine) Rhombenikosidodekaeder besitzt als Ausgangskörper den Dodekaeder.

Er kann durch Abstumpfung entstehen


Der (Kleine) Rhombenikosidodekaeder besitzt

     120 Ecken,

     60 Kanten und

     62 Flächen

und besteht aus 20 Dreiecken, 30 Quadraten und 12 Fünfecken.

Großes Rhombenikosidodekaeder

Großes Rhomenikosidodekaeder.png

Dodecahedron.svg «» Großes Rhomenikosidodekaeder.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der (Kleine) Rhombenikosidodekaeder besitzt als Ausgangskörper den Dodekaeder.

Er kann durch Abstumpfung entstehen


Der (Kleine) Rhombenikosidodekaeder besitzt

     180 Ecken,

     120 Kanten und

     62 Flächen

und besteht aus 30 Quadraten, 20 Sechsecken, 12 Zehnecken.

Abgeschrägtes Dodekaeder

Abgeschrägte Dodekaeder Variante 1.png

Dodecahedron.svg «» Abgeschrägte Dodekaeder Variante 1.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Abgeschrägte Dodekaeder 1 besitzt als Ausgangskörper den Dodekaeder.

Er kann durch Abstumpfung entstehen


Der Abgeschrägte Dodekaeder 1 besitzt

     150 Ecken,

     60 Kanten und

     92 Flächen

und besteht aus 80 Dreiecken, 12 Fünfecken.

Abgeschrägtes Dodekaeder Variante 2.png

Dodecahedron.svg «» Abgeschrägtes Dodekaeder Variante 2.png

Abb.: 13.13 Tetraeder «» Tetraederstumpf

Der Abgeschrägte Dodekaeder 2 besitzt als Ausgangskörper den Dodekaeder.

Er kann durch Abstumpfung entstehen


Der Abgeschrägte Dodekaeder 2 besitzt

     150 Ecken,

     60 Kanten und

     92 Flächen

und besteht aus 80 Dreiecken, 12 Fünfecken.





Von „http://rmg.zum.de/index.php?title=Benutzer:Thamm_Pascal/Platonische_Körper/Weiterführende_Inhalte/Archimedische_Körper&oldid=54880“

Navigationsmenü