Aufgaben zur Laplacewahrscheinlichkeit: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
| + | <div class="lueckentext-quiz" >Ordne nach der Wahrscheinlichkeit, dass das jeweilige Ereignis beim Würfelwurf eintritt | ||
| + | P('''Augenzahl ist 7''') < | ||
| + | P('''Augenzahl ist kleiner oder gleich 2''') < | ||
| + | P('''Augenzahl ist gerade''') < | ||
| + | P('''Augenzahl ist kleiner 7''') | ||
| + | |||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | ==== <u>Achtung:</u> Es können auch mehrere Antworten oder auch keine Antwort richtig sein! ==== | ||
| + | |||
| + | Mit welcher Wahrscheinlichkeit wird mit einem Würfel eine 1 gewürfelt? | ||
| + | (!<math>\frac{3}{2} </math>) (<math>\frac{1}{6} </math>) (!<math>\frac{1}{2} </math>) (!<math>\frac{6}{1} </math>) | ||
| + | |||
| + | Es werden ein blauer und ein roter Würfel geworfen. P(11)= <math>\frac{Maechtigkeit von 11}{Maechtigkeit von 2;3;4;5;6;7;8;9;10;11;12} </math> = <math>\frac{1}{11} </math>. | ||
| + | |||
| + | Finde den Fehler! | ||
| + | (!Es gibt mehr als 11 mögliche Ergebnisse denn die Würfel werden unterschieden: P = <math>\frac{1}{36} </math>) (!Es gibt mehr als 11 mögliche Ergebnisse denn die Würfel werden unterschieden: P = <math>\frac{1}{21} </math>) (Es gibt mehr als 11 mögliche Ergebnisse: P = <math>\frac{2}{36} </math>) | ||
| + | |||
| + | Mit welcher Wahrscheinlichkeit erhält man Kopf beim Münzwurf? | ||
| + | (! <math>\frac{2}{1} </math>) (<math>\frac{1}{2} </math>) | ||
| + | |||
| + | Wie viele Würfelwürfe benötigt man maximal bis man laut Wahrscheinlichkeit die erste 6 hat? | ||
| + | (!1) (!12) (6) (!2) | ||
| + | |||
| + | {| | ||
| + | |width="50%"| | ||
| + | Es werden aus der Urne zwei Kugeln ohne zurücklegen gezogen. Mit welcher Wahrscheinlichkeit ist die erste Kugel rot? | ||
| + | |||
| + | |width="3%"| | ||
| + | |||
| + | |valign="top"|[[Datei:Urne Internet.jpg|100px]] | ||
| + | |} | ||
| + | (<math>\frac{3}{5} </math>) (!<math>\frac{2}{5} </math>) (!<math>\frac{1}{2} </math>) | ||
| + | |||
| + | Nun wurde eine blaue Kugel gezogen. Mit welcher Wahrscheinlichkeit ist die Kugel jetzt rot? | ||
| + | (<math>\frac{3}{4} </math>) (!<math>\frac{3}{5} </math>) (!<math>\frac{1}{2} </math>) | ||
| + | |||
| + | Mit welcher Wahrscheinlichkeit würfelt man eine 8 bei zwei gleichen Würfeln? | ||
| + | (!<math>\frac{1}{36} </math>)(!<math>\frac{3}{36}</math>)(<math>\frac{3}{21} </math>) (!<math>\frac{1}{21} </math>) | ||
| + | |||
| + | Wie viele Ereignisse gibt es bei 2 Würfeln mehr, wenn man diese unterscheidet? | ||
| + | (!0) (15) (!1) (!2) (!13) | ||
| + | |||
| + | Welches dieser Experimente ist kein Laplace-Experiment? | ||
| + | (!Wurf eines Würfels) (!Experiment mit einem möglichen Ergebnis) | ||
| + | |||
| + | Welche Zahl wird mit der höchsten Wahrscheinlichkeit bei 2 gleichen Würfeln geworfen? | ||
| + | (!1) (!2) (!3) (!4) (!5) (6) (7) (8) (!9) (!10) (!11) (!12) | ||
| + | |||
| + | Welche Zahl wird mit der geringsten Wahrscheinlichkeit bei 2 gleichen Würfeln geworfen? | ||
| + | (1) (!2) (!3) (!4) (!5) (!6) (!7) (!8) (!9) (!10) (!11) (!12) | ||
| + | |||
| + | </div> | ||
| Zeile 33: | Zeile 91: | ||
''Andere Seiten:'' | ''Andere Seiten:'' | ||
<br /> | <br /> | ||
| − | [[Kurzbiographie von Pierre-Simon Laplace]] - [[Erklärung der Laplacewahrscheinlichkeit]] - [[weitere Links]] - [[Benutzer: Patrick Reh|zurück]]</div> | + | [[Kurzbiographie von Pierre-Simon Laplace]] - [[Erklärung der Laplacewahrscheinlichkeit]] - [[weitere Links]] - [[Warum die Laplacewahrscheinlichkeit?]] - [[Benutzer: Patrick Reh|zurück]]</div> |
 ) (
) ( ) (!
) (! ) (!
) (! )
)
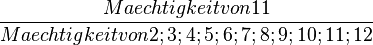 =
= 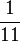 .
.
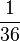 ) (!Es gibt mehr als 11 mögliche Ergebnisse denn die Würfel werden unterschieden: P =
) (!Es gibt mehr als 11 mögliche Ergebnisse denn die Würfel werden unterschieden: P = 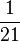 ) (Es gibt mehr als 11 mögliche Ergebnisse: P =
) (Es gibt mehr als 11 mögliche Ergebnisse: P = 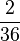 )
)
 ) (
) (
 ) (!
) (! ) (!
) (! ) (!
) (!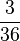 )(
)(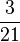 ) (!
) (!
