Tonraumzahlen2: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: ===Beweis der Rechenregeln für den Logarithmus=== <br><br>Da dies nur Einzelbeispiele sind, sind die Rechenregeln nun zu beweisen (Aufbauend auf den Potenzgesetzen. E...)
 
(→‎Beweis der Rechenregeln für den Logarithmus)
 
Zeile 45: Zeile 45:
 
Analog ist <br><br> <div style = "border: 2px solid red; padding:0.75em;"> <math>\frac {1}{2} \cdot \log \ u = \log \ \sqrt{u}</math><br></div><br><br>, da <math>\sqrt {u} = u^{0{,}5}</math> ist, also der letzte Beweis angewendet werden kann.<br><br>
 
Analog ist <br><br> <div style = "border: 2px solid red; padding:0.75em;"> <math>\frac {1}{2} \cdot \log \ u = \log \ \sqrt{u}</math><br></div><br><br>, da <math>\sqrt {u} = u^{0{,}5}</math> ist, also der letzte Beweis angewendet werden kann.<br><br>
  
−
[[Benutzer:Grieninger_Sebastian/Facharbeit/Cent-System| ''' weiter zum Cent-System''']]
+
[[Benutzer:Grieninger_Sebastian/Facharbeit/Cent-System| ''' weiter zum Cent-System''']]<br><br>
 +
[[Benutzer:Grieninger_Sebastian/Facharbeit|zurück zur Übersichtsseite]]

Aktuelle Version vom 20. Dezember 2010, 02:09 Uhr

Beweis der Rechenregeln für den Logarithmus



Da dies nur Einzelbeispiele sind, sind die Rechenregeln nun zu beweisen (Aufbauend auf den Potenzgesetzen. Eine Einführung zu den Potenzgesetzen findet sich hier):

Der Logarithmus ist wie folgt definiert:

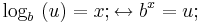
\log_b \ (u) = x; \leftrightarrow b^x = u;
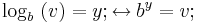
\log_b \ (v) = y; \leftrightarrow b^y = v;


Für das Produkt folgt:

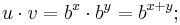
u \cdot v = b^x \cdot b^y = b^{x+y};

Wenn man wieder die Definition des Logarithmus anwendet erhält man:

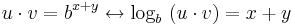
u \cdot v = b^{x+y} \leftrightarrow \log_b \ (u \cdot v) = x + y

Wenn nun x und y durch die Werte von oben wieder ersetzt wird, bekommt man:

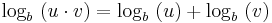
\log_b \ (u \cdot v) = \log_b \ (u) + \log_b \ (v)


Analog folgt für den Quotienten 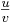\textstyle \frac {u}{v}:

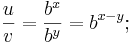
\frac {u}{v} = \frac {b^x}{b^y} = b^{x-y};

Anwendung der Definition des Logarithmus:

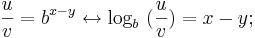
\frac {u}{v} = b^{x - y} \leftrightarrow \log_b \ (\frac {u}{v}) = x - y;

x und y ersetzen:

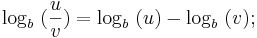
\log_b \ (\frac {u}{v}) = \log_b \ (u) - \log_b \ (v);


Das Vorziehen des Exponenten:

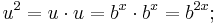
u^2 = u \cdot u = b^x \cdot b^x = b^{2x};

Anwendung der Definition des Logarithmus:

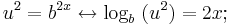
u^2 = b^{2x} \leftrightarrow \log_b \ (u^2) = 2x;

x ersetzen:

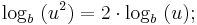
\log_b \ (u^2) = 2 \cdot \log_b \ (u);


Analog ist

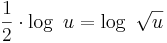
\frac {1}{2} \cdot \log \ u = \log \ \sqrt{u}


, da 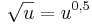\sqrt {u} = u^{0{,}5} ist, also der letzte Beweis angewendet werden kann.

weiter zum Cent-System

zurück zur Übersichtsseite

Von „http://rmg.zum.de/index.php?title=Benutzer:Grieninger_Sebastian/Facharbeit/Tonraumzahlen2&oldid=39277“