Asymmetrische Kryptographie: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="text-align:right;">[[Bild:Buch.PNG]][[Benutzer:Deininger_Matthias/Facharbeit/Fachwortverzeichnis| Fachwortverzeichnis]]</div> | ||
=== Asymmetrische Kryptographie=== | === Asymmetrische Kryptographie=== | ||
<br> | <br> | ||
Der RSA-Algorithmus kann als asymmetrisch bezeichnet werden, weil im Gegensatz zum symmetrischen Verfahren, nicht ein geheimer Schlüssel zur Ver- und Entschlüsselung verwendet wird, sondern jeder Benutzer zwei Schlüssel besitzt. Alice hat also einen öffentlichen und einen privaten Schlüssel.<br> | Der RSA-Algorithmus kann als asymmetrisch bezeichnet werden, weil im Gegensatz zum symmetrischen Verfahren, nicht ein geheimer Schlüssel zur Ver- und Entschlüsselung verwendet wird, sondern jeder Benutzer zwei Schlüssel besitzt. Alice hat also einen öffentlichen und einen privaten Schlüssel.<br> | ||
| − | Der öffentliche Schlüssel oder Public-Key, der asymmetrischen Verfahren den Namen Public-Key-Kryptographie gab, kann von anderen, in unserem Fall von Bob, dazu genutzt werden, Nachrichten an den Besitzer des öffentlichen Schlüssels (hier: Alice) zu verschlüsseln. Ihren öffentlichen Schlüssel darf Alice jedem geben, im Gegensatz zum | + | Der öffentliche Schlüssel oder ''Public-Key'', der asymmetrischen Verfahren den Namen ''Public-Key-Kryptographie'' gab, kann von anderen, in unserem Fall von Bob, dazu genutzt werden, Nachrichten an den Besitzer des öffentlichen Schlüssels (hier: Alice) zu verschlüsseln. Ihren öffentlichen Schlüssel darf Alice jedem geben, im Gegensatz zum zweiten, dem privaten Schlüssel oder ''Private-Key'', den im Idealfall nur sie kennt. Mithilfe des privaten Schlüssels hat Alice die Möglichkeit, die Nachrichten von Bob zu entschlüsseln und anschließend zu lesen, ohne dass die beiden dazu unverschlüsselt geheime Daten übertragen mussten.<br> |
<br> | <br> | ||
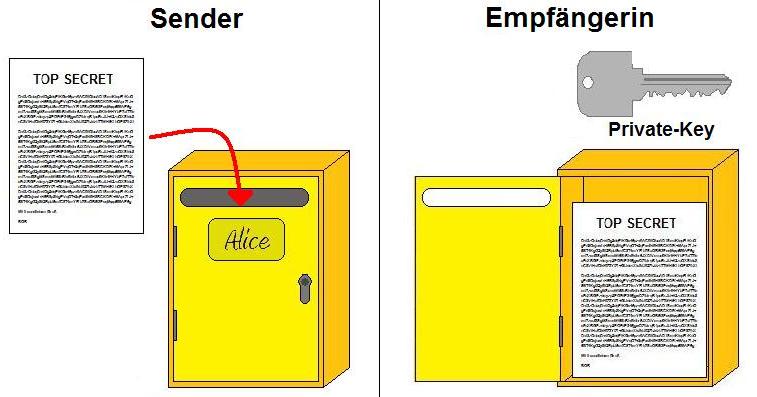
Ein anschauliches Beispiel für den gerade beschriebenen Ver- und Entschlüsselungsvorgang stellt der Postkasten dar:<br> | Ein anschauliches Beispiel für den gerade beschriebenen Ver- und Entschlüsselungsvorgang stellt der Postkasten dar:<br> | ||
<br> | <br> | ||
| − | <div style="text-align:center">[[Bild:Deininger Matthias_Asym_Verschluesselung.jpg | + | <div style="text-align:center">[[Bild:Deininger Matthias_Asym_Verschluesselung.jpg]][[Bild:Alice_lächelnd.jpg]]</div> |
<br> | <br> | ||
| − | „Das Einwerfen eines Briefes entspricht der Chiffrierung mit dem öffentlichen Schlüssel; jeder kann das tun.“<ref name="t9">[9, S. 37]</ref> Ist die Post im Briefkasten ist es fast niemandem mehr möglich den Brief zu lesen, denn „die Post aus dem Briefkasten wieder herauszubekommen, entspricht der Dechiffrierung mit dem privaten Schlüssel.“<ref name="t9"/> und da normalerweise nur Alice ihren privaten Schlüssel besitzt, sollte nur sie den Briefkasten öffnen und die Nachrichten lesen können.<br> | + | „Das Einwerfen eines Briefes entspricht der Chiffrierung mit dem öffentlichen Schlüssel; jeder kann das tun.“<ref name="t9">[9, S. 37]</ref> Ist die Post im Briefkasten, ist es fast niemandem mehr möglich den Brief zu lesen, denn „die Post aus dem Briefkasten wieder herauszubekommen, entspricht der Dechiffrierung mit dem privaten Schlüssel.“<ref name="t9"/> und da normalerweise nur Alice ihren privaten Schlüssel besitzt, sollte nur sie den Briefkasten öffnen und die Nachrichten lesen können.<br> |
<br> | <br> | ||
| − | Somit kann durch das RSA-Verfahren eine Kommunikation zwischen Alice und Bob stattfinden, ohne | + | Somit kann durch das RSA-Verfahren eine Kommunikation zwischen Alice und Bob stattfinden, ohne dass Mallory herausfinden kann, über was sie sprechen.<br> |
<br> | <br> | ||
Um genau zu verstehen, wie die gerade grob skizzierte Verschlüsselung mittels RSA funktioniert, sind einige mathematische Grundlagen nötig, die auf den nächsten Seiten vorgestellt werden.<br> | Um genau zu verstehen, wie die gerade grob skizzierte Verschlüsselung mittels RSA funktioniert, sind einige mathematische Grundlagen nötig, die auf den nächsten Seiten vorgestellt werden.<br> | ||
<br> | <br> | ||
| − | [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen| ''' | + | [[Bild:Weiter.png|weiter]] [[Benutzer:Deininger_Matthias/Facharbeit/Mathematische_Grundlagen| '''weiter zu den mathematischen Grundlagen ''']] |
<br> | <br> | ||
<br> | <br> | ||
Aktuelle Version vom 22. Dezember 2010, 23:03 Uhr
Asymmetrische Kryptographie
Der RSA-Algorithmus kann als asymmetrisch bezeichnet werden, weil im Gegensatz zum symmetrischen Verfahren, nicht ein geheimer Schlüssel zur Ver- und Entschlüsselung verwendet wird, sondern jeder Benutzer zwei Schlüssel besitzt. Alice hat also einen öffentlichen und einen privaten Schlüssel.
Der öffentliche Schlüssel oder Public-Key, der asymmetrischen Verfahren den Namen Public-Key-Kryptographie gab, kann von anderen, in unserem Fall von Bob, dazu genutzt werden, Nachrichten an den Besitzer des öffentlichen Schlüssels (hier: Alice) zu verschlüsseln. Ihren öffentlichen Schlüssel darf Alice jedem geben, im Gegensatz zum zweiten, dem privaten Schlüssel oder Private-Key, den im Idealfall nur sie kennt. Mithilfe des privaten Schlüssels hat Alice die Möglichkeit, die Nachrichten von Bob zu entschlüsseln und anschließend zu lesen, ohne dass die beiden dazu unverschlüsselt geheime Daten übertragen mussten.
Ein anschauliches Beispiel für den gerade beschriebenen Ver- und Entschlüsselungsvorgang stellt der Postkasten dar:
„Das Einwerfen eines Briefes entspricht der Chiffrierung mit dem öffentlichen Schlüssel; jeder kann das tun.“[1] Ist die Post im Briefkasten, ist es fast niemandem mehr möglich den Brief zu lesen, denn „die Post aus dem Briefkasten wieder herauszubekommen, entspricht der Dechiffrierung mit dem privaten Schlüssel.“[1] und da normalerweise nur Alice ihren privaten Schlüssel besitzt, sollte nur sie den Briefkasten öffnen und die Nachrichten lesen können.
Somit kann durch das RSA-Verfahren eine Kommunikation zwischen Alice und Bob stattfinden, ohne dass Mallory herausfinden kann, über was sie sprechen.
Um genau zu verstehen, wie die gerade grob skizzierte Verschlüsselung mittels RSA funktioniert, sind einige mathematische Grundlagen nötig, die auf den nächsten Seiten vorgestellt werden.
![]() weiter zu den mathematischen Grundlagen
weiter zu den mathematischen Grundlagen
Wer bereits mit dem Euklidischen Algorithmus, der Modulo-Rechnung und dem Satz von Euler vertraut ist oder wer sich nicht zu detailliert mit der Mathematik, die sich hinter dem RSA-Verfahren verbirgt, beschäftigen möchte, der kann hier gleich mit dem RSA-Algorithmus fortfahren.
![]() weiter zum RSA-Algorithmus
weiter zum RSA-Algorithmus
zurück zur Übersicht