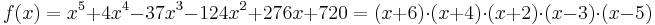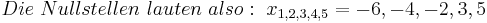Einwegfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: === Einwegfunktion (one-way-function oder preimage resistant function) === <br> Eine Einwegfunktion ist „eine Funktion, die einfach zu berechnen ist, deren Umkehrung...) |
|||
| (14 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | === Einwegfunktion (one-way-function oder preimage resistant function) === | + | <div style="text-align:right;">[[Bild:Buch.PNG]][[Benutzer:Deininger_Matthias/Facharbeit/Fachwortverzeichnis| Fachwortverzeichnis]]</div> |
| + | === Einwegfunktion (''one-way-function'' oder ''preimage resistant function'') === | ||
<br> | <br> | ||
| − | Eine Einwegfunktion ist | + | Eine Einwegfunktion ist „[e]ine Funktion, die einfach zu berechnen ist, deren Umkehrung jedoch nur mit großem Aufwand berechnet werden kann [...]“.<ref>[8, S.168]</ref><br> |
<br> | <br> | ||
| − | + | Eine anschauliche Analogie aus dem Alltag stellt das Telefonbuch (in gedruckter Form) dar. Es ist denkbar einfach für Bob zu einem gegebenen Namen eine Telefonnummer zu finden, da das Telefonbuch alphabetisch geordnet ist. Es ist jedoch nahezu unmöglich für Bob, zu einer von Alice beliebig ausgewählten Nummer den Besitzer zu ermitteln. <br> | |
<br> | <br> | ||
Ein weiteres Beispiel hierfür sind Polynome fünften Grades oder höher, denn für sie gibt es kein allgemeines Modell, mithilfe dessen sich die Nullstellen einfach bestimmen ließen. Erhält man jedoch die Nullstellen, so kann man ganz einfach durch Ausmultiplizieren das Polynom in Summenschreibweise erzeugen.<br> | Ein weiteres Beispiel hierfür sind Polynome fünften Grades oder höher, denn für sie gibt es kein allgemeines Modell, mithilfe dessen sich die Nullstellen einfach bestimmen ließen. Erhält man jedoch die Nullstellen, so kann man ganz einfach durch Ausmultiplizieren das Polynom in Summenschreibweise erzeugen.<br> | ||
<br> | <br> | ||
Beispiel:<br> | Beispiel:<br> | ||
| − | Diesmal fordert Bob von Alice | + | Diesmal fordert Bob von Alice die Nullstellen der Funktion zu bestimmen: <br> |
<br> | <br> | ||
| − | <math>x^5+4x^4-37x^3-124x^2+276x+720 </math><br> | + | <math>f(x)=x^5+4x^4-37x^3-124x^2+276x+720 </math><br> |
<br> | <br> | ||
| − | Kannst | + | Kannst du ihr helfen?<br> |
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | <math>x^5+4x^4-37x^3-124x^2+276x+720 = (x+6)\cdot (x+4)\cdot (x+2)\cdot (x-3)\cdot (x-5)</math><br><br> | + | <math>f(x)=x^5+4x^4-37x^3-124x^2+276x+720 = (x+6)\cdot (x+4)\cdot (x+2)\cdot (x-3)\cdot (x-5)</math><br><br> |
<math>Die\ Nullstellen\ lauten\ also:\ x_{1,2,3,4,5}= -6,-4,-2,3,5</math> | <math>Die\ Nullstellen\ lauten\ also:\ x_{1,2,3,4,5}= -6,-4,-2,3,5</math> | ||
| + | <ggb_applet width="383" height="307" version="3.2" ggbBase64="UEsDBBQACAAIANJLLD0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVdZb+M2EH7u/gqCBRZJWys8dFhdaxe5UATYC8h2H/pQgJZom40kuhKVyPn1HZKSY7sH0m3aVIBBzcHhzDcH5dmbvirRrWxapesM04BgJOtcF6peZrgzi8kUv3n9YraUeinnjUAL3VTCZJgHDFt+p16/+GrWrvQdEqVT+azkXYYXomwlRu26kaJoV1KaPb7oelUq0Ww+zH+RuWkfBN7IVb3u4BTTdMDLq+KtakfyxB24LpW5ULeqkA0qdZ7hOALX4e2zbIzKRZnhkHgOA2/jZE9oWVa60o2617Wx6g/GF8BBqFX3EhBhljc7cYHOZJeXqlCitsE4P0AJoTtVmBWYnHIwKdVyZQEikbeWa90U15vWyAr1P8lGZ5iRJOAkDJOU8illURRitBlFaRCzNIUfpyQNaQwggsfgCpsGZBqnIaEkSXjICcS0GWQkoIwd7HOny9traQxks0Wil+0I6bJRxRZzS1y1Z7p8YK21qs25WJuucZXAB9a12bjjMGpsmKf1spQDj0GiVjK/mev+2kPHvelPm7Xb4vyZL891qRvUwIYoAoVhnfvV6VhHt1rE6RCnMdiwRrdymjKn4da5X51WqWrv2hA4HaOmZDxGtcgywLgt4BGbUswl1ANGXa3M25GAurkZIqVe/31XzaFxditna5I+kcnZyUHJzW5kU8vSF1YNie1016JbW8A+dc6PQuaqAtILBkCETdaP4IDnFnLZyNFv33UeLiclu8V7wJ6djE5YH1rwNTcwPiAeY2P5qMtNrSsUBT80opCt7XYDnZbhC6lqKCdo2XfCmJUSICuEgT12lsgehkVrB5HHC0FIMI36NaxH/THKUP/zURSQY/QtCgOCvrF0aOkJ4snI4J5B2VaF+S0siT0H3hNGAh+KLGUlod2NK9JFV7tQthlb4P1SAqfzmxq8dPVudivbzUDtxtlB2h/qA8R/Utgw+NYrYRt5MFeKDeC0mwtn7Z0u9jMkasi0gx8mzNpNAjt2pSyGcT46idZg0jXzTqE8IjIoQY+RS3dVibpAtahAfFUbKFaI14Gk7MhGgrisCZrh/hS6YYi7M6Pw1AvPYIEpfA4Lh8KAJczwpT9vOOV32XETaIvqKf4S1Meh849xd53Roj7Dk9jCvPE20L2H3en4kWmvCLeTH8L5V+Gd/afhfVgsWml8NC6WCX1k8NBmew9z28MgCpMw4RGZTuMwDunlxF4HTwXO+XOBM/174NAg3X/8fhpQHk/jKU8SRmMaE/608Fw8Fzyhh4c9Dh7+b/TN5f9lLERfHN3BPZjhT7I3dLgKX/7aafPqfVeWMO/LUtbfv/yaklen6GgSf4fIsaPOgAq31DlQbEtdoCO+JS7RUeQIZ/UPbkQDR+N9P57xsmuNaMxHix8aJi98c6ck5RymDUvCob3ChAVpnMQkJglhLEx2E7AL9cnu94v7zB/+57z+DVBLBwhTC0tZPAQAABkNAABQSwECFAAUAAgACADSSyw9UwtLWTwEAAAZDQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAHYEAAAAAA==" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
</popup> | </popup> | ||
| + | <br> | ||
| + | [[Benutzer:Deininger_Matthias/Facharbeit/Faktorisierungsproblem| '''zurück zum Lernpfad''']] | ||
| + | <br> | ||
| + | <br> | ||
| + | [[Benutzer:Deininger_Matthias/Facharbeit| zurück zur Übersicht]] | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | ---- | ||
| + | <references /> | ||
Aktuelle Version vom 23. Dezember 2010, 02:58 Uhr
Einwegfunktion (one-way-function oder preimage resistant function)
Eine Einwegfunktion ist „[e]ine Funktion, die einfach zu berechnen ist, deren Umkehrung jedoch nur mit großem Aufwand berechnet werden kann [...]“.[1]
Eine anschauliche Analogie aus dem Alltag stellt das Telefonbuch (in gedruckter Form) dar. Es ist denkbar einfach für Bob zu einem gegebenen Namen eine Telefonnummer zu finden, da das Telefonbuch alphabetisch geordnet ist. Es ist jedoch nahezu unmöglich für Bob, zu einer von Alice beliebig ausgewählten Nummer den Besitzer zu ermitteln.
Ein weiteres Beispiel hierfür sind Polynome fünften Grades oder höher, denn für sie gibt es kein allgemeines Modell, mithilfe dessen sich die Nullstellen einfach bestimmen ließen. Erhält man jedoch die Nullstellen, so kann man ganz einfach durch Ausmultiplizieren das Polynom in Summenschreibweise erzeugen.
Beispiel:
Diesmal fordert Bob von Alice die Nullstellen der Funktion zu bestimmen:
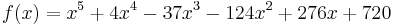
Kannst du ihr helfen?
zurück zum Lernpfad
zurück zur Übersicht
- ↑ [8, S.168]