Grundwissenübersicht - Alles auf einen Blick: Unterschied zwischen den Versionen
Aus RMG-Wiki
K |
(link angepasst) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 46: | Zeile 46: | ||
* a + (b - c) = a + b - c | * a + (b - c) = a + b - c | ||
* a - (b + c) = a - b - c | * a - (b + c) = a - b - c | ||
| − | * a - (b - c) = a - b | + | * a - (b - c) = a - b + c |
* (a + b) • (c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd | * (a + b) • (c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd | ||
* (a - b) • (c + d) = a(c + d) - b(c + d) = ac + ad - bc - bd | * (a - b) • (c + d) = a(c + d) - b(c + d) = ac + ad - bc - bd | ||
| Zeile 53: | Zeile 53: | ||
</div> | </div> | ||
<br /><br /> | <br /><br /> | ||
| − | [[ | + | [[Lernpfad Terme|Zurück zur Übersicht]] |
Aktuelle Version vom 26. Februar 2011, 18:31 Uhr
Diese Grundwissenseite dient als Übersicht über die wichtigsten Begriffe im Zusammenhang mit Termen.
Grundwissen Terme - Alles auf einen Blick
Inhaltsverzeichnis |
Begriffe
Term
Ein Term ist ein Rechenausdruck, der einen Sachverhalt beschreibt und neben Zahlen auch Variablen enthalten kann.
Variable
Eine Variable ist ein Platzhalter (häufig Buchstaben), der durch verschiedene Einsetzungen ausgetauscht werden kann.
Definitionsmenge
Die Definitionsmenge ist die Menge der Zahlen, die bei der Einsetzung für eine Variable in einen Term zu einer sinnvollen Aussage führen.
Termwert
Der Termwert ist das Ergebnis, das man erhält, wenn man in den Term eine Zahl der Definitionsmenge einsetzt.
Termart
Die Termart wird durch das letzte ausgeführte Rechenzeichen festgelegt.(mehr Information)
Rechengesetze
Kommutativgesetz
- a + b = b + a
- a • b = b • a
- für alle a, b, c,

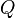
Assoziativgesetz
- a + (b + c) = (a + b) + c = a + b + c
- a • (b • c) = (a • b) • c = a • b • c
- für alle a, b, c,

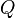
Distributivgesetz
- a • (b + c) = a • b + a • c
- a • (b - c) = a • b - a • c
- für alle a, b, c,

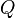
-
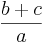 =
= 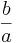 +
+ 
- bzw. (b + c) : a = b : a + c : a
-
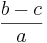 =
= 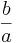 -
- 
- bzw. (b - c) : a = b : a - c : a
- für alle a, b, c,

 ; (a
; (a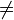 0)
0)
- für alle a, b, c,
Klammerregeln
- a + (b + c) = a + b + c
- a + (b - c) = a + b - c
- a - (b + c) = a - b - c
- a - (b - c) = a - b + c
- (a + b) • (c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd
- (a - b) • (c + d) = a(c + d) - b(c + d) = ac + ad - bc - bd
- (a + b) • (c - d) = a(c - d) + b(c - d) = ac - ad + bc - bd
- (a - b) • (c - d) = a(c - d) - b(c - d) = ac - ad - bc + bd

