weitere Aufgaben: Unterschied zwischen den Versionen
K |
(link angepasst) |
||
| (25 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
|width="40%" style="vertical-align:top"| | |width="40%" style="vertical-align:top"| | ||
Paul baut Dreiecke aus Streichhölzern. Für ein Dreieck braucht er 3 Streichhölzer, für zwei Dreiecke 5, für drei Dreiecke 7 Streichhölzer. (siehe Bild)<br /> | Paul baut Dreiecke aus Streichhölzern. Für ein Dreieck braucht er 3 Streichhölzer, für zwei Dreiecke 5, für drei Dreiecke 7 Streichhölzer. (siehe Bild)<br /> | ||
| − | * Wie viele braucht er für 4 Dreiecke? | + | * Wie viele Streichhölzer braucht er für 4 Dreiecke? |
* Erstelle einen Term, der die Anzahl der benötigten Streichhölzer für x Dreiecke beschreibt. | * Erstelle einen Term, der die Anzahl der benötigten Streichhölzer für x Dreiecke beschreibt. | ||
|width="20%" style="vertical-align:top"| | |width="20%" style="vertical-align:top"| | ||
| Zeile 23: | Zeile 23: | ||
<br /> | <br /> | ||
<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 2:</span>''' | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 2:</span>''' | ||
| − | Finde | + | Finde die Paare |
<div class="memo-quiz"> | <div class="memo-quiz"> | ||
{| | {| | ||
|- | |- | ||
| − | | | + | | 13•x+(-9) || Summe |
|- | |- | ||
| − | | | + | | 13•(x-9) || Produkt |
|- | |- | ||
| − | | | + | | [2(4+y)]:[3(6-y)] || Quotient |
|- | |- | ||
| − | | | + | | (5x<sup>2</sup>+3x+2+7y<sup>2</sup>)-(-<math>\frac{1}{2}</math>) || Differenz |
|} | |} | ||
| − | </div> | + | </div> |
| + | |||
<br /> | <br /> | ||
<br /><br /><br /><br /><br /><br /><br /><br /> | <br /><br /><br /><br /><br /><br /><br /><br /> | ||
| − | Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/ | + | Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/Terme und Variablen/Termarten|Zurück zur Übersicht über die Termarten]] |
</div> | </div> | ||
<br /> | <br /> | ||
| Zeile 44: | Zeile 45: | ||
{|width="99%" | {|width="99%" | ||
|width="40%" style="vertical-align:top"| | |width="40%" style="vertical-align:top"| | ||
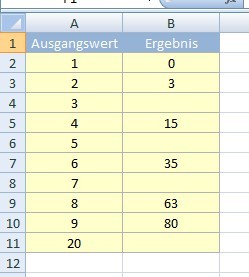
| − | Tina muss einen wichtigen Vortrag halten. Sie musste dazu eine Auswertung mit einem Tabellenkalkulationsprogramm durchführen. Kurz bevor sie ihre Rede halten muss stellt sie fest, dass einige Zahlen in ihrer Auswertung fehlen. Sie überlegt, wie sie die Zahlen bestimmt hat, doch vor lauter Nervosität fällt es ihr | + | Tina muss einen wichtigen Vortrag halten. Sie musste dazu eine Auswertung mit einem Tabellenkalkulationsprogramm durchführen. Kurz bevor sie ihre Rede halten muss stellt sie fest, dass einige Zahlen in ihrer Auswertung fehlen. Sie überlegt, wie sie die Zahlen bestimmt hat, doch vor lauter Nervosität fällt es ihr nicht mehr ein. |
* Finde die Formel! | * Finde die Formel! | ||
* Suche nach einem Ausgangswert, bei dem sich das Ergebnis 120 ergibt. | * Suche nach einem Ausgangswert, bei dem sich das Ergebnis 120 ergibt. | ||
| Zeile 53: | Zeile 54: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
* T(x)= x<sup>2</sup> - 1 | * T(x)= x<sup>2</sup> - 1 | ||
| − | * T(11)= 11<sup>2</sup> -1 = | + | * T(11)= 11<sup>2</sup> -1 = 121 - 1 = 120 = T(-11) |
Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/Übersicht/Aufstellen und Interpretieren von Termen|Zurück zu Aufstellen und Interpretieren von Termen]] | Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/Übersicht/Aufstellen und Interpretieren von Termen|Zurück zu Aufstellen und Interpretieren von Termen]] | ||
</popup> </div> | </popup> </div> | ||
| + | <br /> | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 4:</span>''' | ||
| + | Eva hat einen Korb mit x Kirschen. Sie nimmt ein Viertel aus dem Korb heraus und behält sie für sich. Dann verschenkt sie zwei Siebtel der restlichen Kirschen an Kai. Die Kirschen, die sie dann noch übrig hat, verschenkt sie zu gleichen Teilen an Tom und Nina. | ||
| + | X sei die Anzahl der Kirschen, die zu Beginn im Korb waren. | ||
| + | *Stelle einen Term auf, mit dem du die Anzahl der Kirschen berechnen kannst, die Kai bekommen hat. | ||
| + | *Berechne die Anzahl die Kai bei 56 und 84 Kirschen erhält | ||
| + | *Wie viele Kirschen erhalten bei den oben genannten Zahlen Eva, Tom und Nina? | ||
| + | <popup name="Lösung"> | ||
| + | *T(x)= (x-<math>\frac{1}{4}</math>x) • <math>\frac{2}{7}</math> = <math>\frac{3}{4}</math>x • <math>\frac{2}{7}</math><br /> | ||
| + | * T(56) = (<math>\frac{3}{4}</math> •56) • <math>\frac{2}{7}</math> = 42• <math>\frac{2}{7}</math> = 12 | ||
| + | :T(84) = (<math>\frac{3}{4}</math> •84) • <math>\frac{2}{7}</math> = 63• <math>\frac{2}{7}</math> = 18 | ||
| + | *56 Kirschen: | ||
| + | ::Eva: <math>\frac{56}{4}</math> = 14 | ||
| + | ::Tom: (56-14-12): 2 = 15 | ||
| + | ::Nina: (56-14-12): 2 = 15 <br /> | ||
| + | :84 Kirschen: | ||
| + | ::Eva: <math>\frac{84}{4}</math> = 21 | ||
| + | ::Tom: (84-21-18):2 = 22,5 | ||
| + | ::Nina: (84-21-18):2 = 22,5 | ||
| + | Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/Übersicht/Aufstellen und Interpretieren von Termen|Zurück zu Aufstellen und Interpretieren von Termen]] | ||
| + | </popup> </div> | ||
| + | <br /> | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 5:</span>''' | ||
| + | Klicke auf die Zahlen, um das Kreuzworträtsel zu füllen. | ||
| + | <div class="kreuzwort-quiz"> | ||
| + | {| | ||
| + | |- | ||
| + | | Variable || Platzhalter (anderer Begriff) | ||
| + | |- | ||
| + | | Differenz || (2+x)-(4+3y); Termart | ||
| + | |- | ||
| + | | Termwert || Ergebnis eines Terms | ||
| + | |- | ||
| + | | Termart || Quotient, Differenz, Summe und Produkt | ||
| + | |- | ||
| + | | Vorrangregel || Klammer zuerst, Potenz vor Punkt vor Strich | ||
| + | |- | ||
| + | | Quotient || Der Divisor ist Teil des | ||
| + | |- | ||
| + | | Distributivgesetz || a•(b+c) = a•b + a•c (Rechengesetz) | ||
| + | |- | ||
| + | | Kommutativgesetz || a+b = b+a (Rechengesetz) | ||
| + | |- | ||
| + | | Summe || (a+b)+(c+d); Termart | ||
| + | |} | ||
| + | </div> | ||
| + | <br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> | ||
| + | Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/Übersicht/Terme und Variablen|Zurück zu Terme und Variablen]] | ||
| + | </div> | ||
| + | <br /> | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 6:</span>''' | ||
| + | Ordne die Beschreibungen den Umformungsschritten zu. | ||
| + | |||
| + | <div class="lueckentext-quiz"> | ||
| + | {| class="wikitable center" | ||
| + | |- | ||
| + | | 9•(3x+4) - (8x+5)•3 = || = (27x+36) - (24x+15) = || = 27x+36-24x-15 = || = 27x-24x+36-15 = || = 3x+21 = || = 3(x+7) | ||
| + | |- | ||
| + | | <strong> Klammern ausmultiplizieren </strong> || <strong> Klammern auflösen, "Minusklammer" beachten </strong> || <strong> Ordnen, durch Anwendung des KG </strong> || <strong> Zusammenfassen </strong> || <strong> Faktorisieren </strong> | ||
| + | |- | ||
| + | |}</div><br /> | ||
| + | <br /><br /><br /><br /><br /> | ||
| + | Schwierigkeiten gehabt? [[Facharbeit Lernpfad Terme/Übersicht/Auflösen von Klammern|Zurück zu Auflösen von Klammern]] | ||
| + | </div> | ||
| + | |||
| + | <br /><br /><br /> | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 7:</span>''' | ||
| + | <br /> | ||
| + | <span style="color: orange">'''Abschlusstest:'''</span> | ||
| + | Dieser Multiple Choice Test ist die letzte Aufgabe des Lernpfades. Aus jedem Themengebiet werden Aufgaben gestellt, bei denen mehrere Antworten richtig sein können. Kreuze also alles an, was du für richtig hälst. Wenn du eine Aufgabe nicht lösen kannst, solltest du dir das entsprechende Kapitel noch einmal anschauen. | ||
| + | <quiz display="simple"> | ||
| + | {Der Term T(x) = x<sup>2</sup>-4 ist... und äquivalent zu} | ||
| + | - ein Produkt | ||
| + | - eine Summe | ||
| + | - ein Quotient | ||
| + | + eine Differenz | ||
| + | |||
| + | - (x - 2)(x - 2) | ||
| + | + (x - 2)(x + 2) | ||
| + | - (x + 2)(x + 2) | ||
| + | |||
| + | {Der Term T(a) = a<sup>2</sup>-2a-3 ist} | ||
| + | + ein Produkt aus (a+1)(a-3) | ||
| + | + eine Differenz aus a<sup>2</sup>-(2a+3) | ||
| + | - eine Summe aus (a<sup>2</sup>+2)+(a+3) | ||
| + | - ein Quotient aus (a<sup>2</sup>+1):(a<sup>2</sup>-2)+3a | ||
| + | |||
| + | {Um den Term T<sub>1</sub>(x) = 4(2x+4)+(6x-8)4 in die Form T<sub>2</sub>(x)= 16(2x-1) zu bringen muss man:} | ||
| + | + zusammenfassen | ||
| + | + KG anwenden | ||
| + | - mit 9 multiplizieren | ||
| + | - AG anwenden | ||
| + | + ausklammern | ||
| + | - kürzen | ||
| + | + ausmultiplizieren | ||
| + | - durch 3 dividieren | ||
| + | - mit 0,5 multiplizieren | ||
| + | |||
| + | {Familie Fuchs tauscht ihren quadratischen Bauplatz gegen einen rechteckigen, der 4m breiter, aber auch 4m kürzer ist. Welcher Bauplatz hat den größeren Flächeinhalt?} | ||
| + | - der rechteckige | ||
| + | + der quadratische | ||
| + | |||
| + | {In der Firma MathIntelligent erhält jeder Angestellte eine Formel, nach der sein Lohn berechnet wird. Dafür wird für die Variable die Anzahl der Monate eingesetzt, die der Angestellte schon dort arbeitet und das berechnete Ergebnis wird mit dem Faktor 2000€ überwiesen. Die neue Angestellte, die für 6 Monate dort arbeiten darf, erhält folgende drei Angebote. Welches sollte sie wählen, um in ihren 3 Monaten Arbeitszeit insgesamt den größten Verdienst zu erhalten?} | ||
| + | + V<sub>1</sub>(x) = <math>\frac{15}{x}</math> | ||
| + | - V<sub>2</sub>(x) = <math>\frac{1}{5}</math>x<sup>2</sup> -x+4 | ||
| + | - V<sub>3</sub>(x) = 0,2x+6 | ||
| + | |||
| + | |||
| + | </quiz> | ||
| + | </div> | ||
| + | <br /><br /><br /><br /><br /> | ||
| + | '''<span style="color: darkgreen">Toll! Die weiteren Aufgaben hast du jetzt auch noch gemacht! Zum Schluss gibt's noch eine [[Lernpfad Terme/Grundwissenübersicht - Alles auf einen Blick|Grundwissenübersicht]] für dich!</span>''' | ||
| + | [[Bild:schnecke_vorwort.gif]] | ||
| + | <br /><br /> | ||
| + | [[Lernpfad Terme|Zurück zur Übersicht]] | ||
Aktuelle Version vom 26. Februar 2011, 18:30 Uhr
Die folgenden Aufgaben sind für alle, die schon fertig sind oder noch weiter üben wollen. Wenn du bei irgendeiner Aufgabe Probleme hast sie zu lösen, solltest du dir das Kapitel, in der dieser Aufgabentyp behandelt wurde, noch einmal anschaun.
|
Paul baut Dreiecke aus Streichhölzern. Für ein Dreieck braucht er 3 Streichhölzer, für zwei Dreiecke 5, für drei Dreiecke 7 Streichhölzer. (siehe Bild)
|
Finde die Paare
| 13•x+(-9) | Summe |
| 13•(x-9) | Produkt |
| [2(4+y)]:[3(6-y)] | Quotient |
(5x2+3x+2+7y2)-(- ) ) |
Differenz |
Schwierigkeiten gehabt? Zurück zur Übersicht über die Termarten
|
Tina muss einen wichtigen Vortrag halten. Sie musste dazu eine Auswertung mit einem Tabellenkalkulationsprogramm durchführen. Kurz bevor sie ihre Rede halten muss stellt sie fest, dass einige Zahlen in ihrer Auswertung fehlen. Sie überlegt, wie sie die Zahlen bestimmt hat, doch vor lauter Nervosität fällt es ihr nicht mehr ein.
|
Eva hat einen Korb mit x Kirschen. Sie nimmt ein Viertel aus dem Korb heraus und behält sie für sich. Dann verschenkt sie zwei Siebtel der restlichen Kirschen an Kai. Die Kirschen, die sie dann noch übrig hat, verschenkt sie zu gleichen Teilen an Tom und Nina. X sei die Anzahl der Kirschen, die zu Beginn im Korb waren.
- Stelle einen Term auf, mit dem du die Anzahl der Kirschen berechnen kannst, die Kai bekommen hat.
- Berechne die Anzahl die Kai bei 56 und 84 Kirschen erhält
- Wie viele Kirschen erhalten bei den oben genannten Zahlen Eva, Tom und Nina?
Klicke auf die Zahlen, um das Kreuzworträtsel zu füllen.
| Variable | Platzhalter (anderer Begriff) |
| Differenz | (2+x)-(4+3y); Termart |
| Termwert | Ergebnis eines Terms |
| Termart | Quotient, Differenz, Summe und Produkt |
| Vorrangregel | Klammer zuerst, Potenz vor Punkt vor Strich |
| Quotient | Der Divisor ist Teil des |
| Distributivgesetz | a•(b+c) = a•b + a•c (Rechengesetz) |
| Kommutativgesetz | a+b = b+a (Rechengesetz) |
| Summe | (a+b)+(c+d); Termart |
Schwierigkeiten gehabt? Zurück zu Terme und Variablen
Ordne die Beschreibungen den Umformungsschritten zu.
| 9•(3x+4) - (8x+5)•3 = | = (27x+36) - (24x+15) = | = 27x+36-24x-15 = | = 27x-24x+36-15 = | = 3x+21 = | = 3(x+7) |
| Klammern ausmultiplizieren | Klammern auflösen, "Minusklammer" beachten | Ordnen, durch Anwendung des KG | Zusammenfassen | Faktorisieren |
Schwierigkeiten gehabt? Zurück zu Auflösen von Klammern
Abschlusstest:
Dieser Multiple Choice Test ist die letzte Aufgabe des Lernpfades. Aus jedem Themengebiet werden Aufgaben gestellt, bei denen mehrere Antworten richtig sein können. Kreuze also alles an, was du für richtig hälst. Wenn du eine Aufgabe nicht lösen kannst, solltest du dir das entsprechende Kapitel noch einmal anschauen.
Toll! Die weiteren Aufgaben hast du jetzt auch noch gemacht! Zum Schluss gibt's noch eine Grundwissenübersicht für dich!
Zurück zur Übersicht

 x) •
x) •  =
=  x •
x • 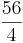 = 14
= 14
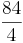 = 21
= 21

