Facharbeit Lernpfad Terme/Addieren und Subtrahieren von Termen: Unterschied zwischen den Versionen
K |
K (→Addieren und Subtrahieren von Termen) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | = <span style="color: green"> | + | = <span style="color: green">Umformen von Termen</span> = |
==<span style="color: green">Äquivalente Terme </span> == | ==<span style="color: green">Äquivalente Terme </span> == | ||
| Zeile 84: | Zeile 84: | ||
:= 3x+5x<sup>2</sup> | := 3x+5x<sup>2</sup> | ||
</popup> </div> | </popup> </div> | ||
| + | <br /><br /> | ||
| + | ==<span style="color: green">Addieren und Subtrahieren äquivalenter Termglieder </span> == | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue"></span>'''Überlege, ob du folgende Terme vereinfachen kannst: | ||
| + | *5•x+3•x= | ||
| + | *5•x-3•x= | ||
| + | <popup name="Lösung"> | ||
| + | *5•x+3•x= 8•x=8x | ||
| + | <sup><sup>Hochgestellt</sup></sup> | ||
| + | *5•x-3•x= 2•x= 2x | ||
| + | </popup> </div> | ||
| + | <br /> | ||
| + | <div style="orange:0px; margin-right:90px; border: solid orange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: red">Erklärung:</span>''' | ||
| + | Gleichartige Glieder werden addiert, indem man die Koeffizienten addiert und die gemeinsame Variable beibehält: | ||
| + | ::m•x+n•x=(m+n)•x | ||
| + | |||
| + | Gleichartige Glieder werden subtrahiert, indem man vom Koeffizienten des Minuenden den Koeffizienten des Subtrahenden subtrahiert und die gemeinsame Variable beibehält: | ||
| + | ::m•x-n•x=(m-n)•x | ||
| + | </div> | ||
| + | <br /> | ||
| + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Beispiel</span>''' | ||
| + | T(x)= 9•x-6+7•x+8 = 9x+7x-6+8 = 16x+2 | ||
| + | Um einen Term übersichtlicher zu machen, solltest du die Teilterme nach dem Alphabet ordnen und dann die Teilterme mit gleicher Variable zusammenfassen.<br /> | ||
| + | Fasse nun selbst folgende Terme so weit wie möglich zusammen: | ||
| + | |||
| + | * T(z)= 8•z<sup>2</sup>-7+3•z+(4•z<sup>2</sup>+2•z<sup>2</sup>)-2z | ||
| + | * T(n)= 2,2•n+2,8•n<sup>2</sup>-0,25+ <math>\left[ n(2.7+0,3n)\right]</math> | ||
| + | * T(a;b)= 4a<sup>2</sup>-2a+3b+2-8b<sup>2</sup>+a(2b+9) | ||
| + | <popup name="Lösung"> | ||
| + | |||
| + | * T(z)= 8•z<sup>2</sup>-7+3•z+(4•z<sup>2</sup>+2•z<sup>2</sup>)-2z = | ||
| + | := 8z<sup>2</sup>-7+3z+6z<sup>2</sup>-2z = | ||
| + | := 8z<sup>2</sup>+6z<sup>2</sup>+3z-2z-7 = | ||
| + | := 14z<sup>2</sup>+z-7 | ||
| + | * T(n)= 2,2•n+2,8•n<sup>2</sup>-0,25+ <math>\left[ n(2.7+0,3n)\right]</math> = | ||
| + | := 2,2n+2,8n<sup>2</sup>-0,25+ <math>\left[ 2,7n+0,3n^2)\right]</math> = | ||
| + | := 2,2n+2,8n<sup>2</sup>-0,25+2,7n+0,3n<sup>2</sup> = | ||
| + | := 2,8n<sup>2</sup>+0,3n<sup>2</sup>+2,2n+2,7n-0,25 = | ||
| + | := 3,1n<sup>2</sup>+4,9n-0,25 | ||
| + | * T(a;b)= 4a<sup>2</sup>-2a+3b+2-8b<sup>2</sup>+a(2b+9) = | ||
| + | := 4a<sup>2</sup>-2a+3b+2-8b<sup>2</sup>+2ab+9a = | ||
| + | := 4a<sup>2</sup>-2a+9a+2ab-8b<sup>2</sup>+3b+2 = | ||
| + | := 4a<sup>2</sup>+7a+2ab-8b<sup>2</sup>+3b+2 | ||
| + | </popup> </div> | ||
| + | |||
| + | ==<span style="color: green">Übungsaufgaben </span> == | ||
<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>''' | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>''' | ||
Prüfe, ob die Terme äquivalent sind | Prüfe, ob die Terme äquivalent sind | ||
Aktuelle Version vom 14. August 2010, 12:18 Uhr
Inhaltsverzeichnis |
Umformen von Termen
Äquivalente Terme
|
|
Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen heißen gleichwertig oder äquivalent. Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen.
Rechengesetze:
- Kommutativgesetz (KG): für alle rationalen Zahlen a, b gilt:
- a+b = b+a
- a•b = b•a
- Assoziativgesetz (AG): für alle rationalen Zahlen a, b, c gilt:
- a+(b+c) = (a+b)+c = a+b+c
- a•(b•c) = (a•b)•c = a•b•c
- Distributivgesetz (DG): für alle rationalen Zahlen a, b, c gilt:
- a•(b+c) = a•b+a•c
- für alle rationalen Zahlen a, b, c (c
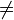 0) gilt:
0) gilt:
- (b+c):a = b:a+c:a
T(a;b)= 3a+(7b+2a)
- (KG)= 3a+(2a+7b)
- (AG)= (3a+2a)+7b
- = 5a+7b
Durch geschicktes Anwenden der Rechengesetze kannst du einen Term zu einem äquivalenten Term vereinfachen. Vereinfache nun selbst folgende Terme:
a)T(a;b)= 7a+(9b+6a)
b)T(a;b)= 2•(a•3)•b+4•(a•5)•b
c)T(a;b)= (3+5•x)•x
Addieren und Subtrahieren äquivalenter Termglieder
Gleichartige Glieder werden addiert, indem man die Koeffizienten addiert und die gemeinsame Variable beibehält:
- m•x+n•x=(m+n)•x
Gleichartige Glieder werden subtrahiert, indem man vom Koeffizienten des Minuenden den Koeffizienten des Subtrahenden subtrahiert und die gemeinsame Variable beibehält:
- m•x-n•x=(m-n)•x
T(x)= 9•x-6+7•x+8 = 9x+7x-6+8 = 16x+2
Um einen Term übersichtlicher zu machen, solltest du die Teilterme nach dem Alphabet ordnen und dann die Teilterme mit gleicher Variable zusammenfassen.
Fasse nun selbst folgende Terme so weit wie möglich zusammen:
- T(z)= 8•z2-7+3•z+(4•z2+2•z2)-2z
- T(n)= 2,2•n+2,8•n2-0,25+
![\left[ n(2.7+0,3n)\right]](/images/math/c/a/c/cac24b41ece2afba3d903683bacaa960.png)
- T(a;b)= 4a2-2a+3b+2-8b2+a(2b+9)
Übungsaufgaben
Prüfe, ob die Terme äquivalent sind
1:
T1 (x)= 5x-2x+6x
T2 (x)= 2•x•2+5x (äquivalent) (!nicht äquivalent)
2 :
T1 (y)= 4y-3•4y+15
T2 (y)= 3•5+2y-4y-6y
(!äquivalent) (nicht äquivalent)
3:
T1 (y;z)= 2y-3+z
T2 (y;z)= 5y•2+z+5-8y-8
(äquivalent) (!nicht äquivalent)
4:
T1 (z)= 4• -2z
-2z
T2 (z)= 6+8z-5•20%-z•9
(!äquivalent) (nicht äquivalent)
5:
T1 (r)= 3r-23 r+5-r
T2 (r)= 3•r•2 (!äquivalent) (nicht äquivalent)
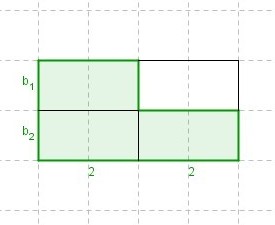
![\left[ 2,7n+0,3n^2)\right]](/images/math/f/4/2/f423bf0c5a84137bb5a2a1e3c3f7eda1.png) =
=

