Facharbeit Lernpfad Terme/Aufstellen und Interpretieren von Termen: Unterschied zwischen den Versionen
K (→Aufstellen von Termen) |
K (→Übungsaufgaben) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
| | | | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild: | + | [[Bild:einstiegsaufg_termaufstellen2.jpg]] <br /> <br /> |
|} | |} | ||
| Zeile 58: | Zeile 58: | ||
| | | | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild: | + | [[Bild:bsptermaufstellen.jpg]] <br /> <br /> |
|} | |} | ||
| Zeile 65: | Zeile 65: | ||
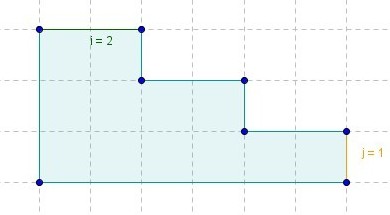
# Untersuchung des Sachverhalts und Suche nach Gesetzmäßigkeit: Es ist eine Figur gegeben, deren Flächeninhalt unbekannt ist. Die Seitenlängen der Figur sind festgelegt. Betrachtet man die Figur, stellt man fest, dass sie aus mehreren kleinen Rechtecken besteht. Der Flächeninhalt eines einzelnen Rechtecks ist A<sub>R</sub> = 2•1. Die Figur besteht aus sechs solchen Rechtecken, also ist der Gesamtflächeninhalt A<sub>F</sub>= 6•2•1 | # Untersuchung des Sachverhalts und Suche nach Gesetzmäßigkeit: Es ist eine Figur gegeben, deren Flächeninhalt unbekannt ist. Die Seitenlängen der Figur sind festgelegt. Betrachtet man die Figur, stellt man fest, dass sie aus mehreren kleinen Rechtecken besteht. Der Flächeninhalt eines einzelnen Rechtecks ist A<sub>R</sub> = 2•1. Die Figur besteht aus sechs solchen Rechtecken, also ist der Gesamtflächeninhalt A<sub>F</sub>= 6•2•1 | ||
| − | # Variablen einführen: Wähle für 2= | + | # Variablen einführen: Wähle für 2=i und für 1=j |
| − | # Term aufstellen und Definitionsmenge überlegen: Der Term lautet: | + | # Term aufstellen und Definitionsmenge überlegen: Der Term lautet: 6•i•j |
| − | : Für die Definitionsmenge gilt: Es ist jede Zahl aus | + | : Für die Definitionsmenge gilt: Es ist jede Zahl aus <math>Q</math> einsetzbar ohne Verstoß gegen die Rechenregeln, bei der Berechnung eines Flächeninhalts ist es jedoch sinnvoll, nur positive Zahlen einzusetzen. Also <math>D</math>=<math>Q</math><sup>+</sup> |
</popup> </div> | </popup> </div> | ||
| Zeile 93: | Zeile 93: | ||
</div> | </div> | ||
| + | <br /> | ||
==<span style="color: green">Übungsaufgaben </span> == | ==<span style="color: green">Übungsaufgaben </span> == | ||
| Zeile 199: | Zeile 200: | ||
* A(15cm;13cm)= 2cm(15cm+13cm)= 2cm•28cm= 56cm<sup>2</sup> | * A(15cm;13cm)= 2cm(15cm+13cm)= 2cm•28cm= 56cm<sup>2</sup> | ||
</popup> </div> | </popup> </div> | ||
| + | <br /><br /> | ||
| + | [[Facharbeit Lernpfad Terme/Umformen von Termen|Weiter zum Kapitel Umformen von Termen]] | ||
| + | <br /> | ||
| + | [[Facharbeit Lernpfad Terme/Übersicht|Zurück zur Übersicht]] | ||
Aktuelle Version vom 19. August 2010, 09:22 Uhr
Inhaltsverzeichnis |
Aufstellen und Interpretieren von Termen
Aufstellen von Termen
|
|
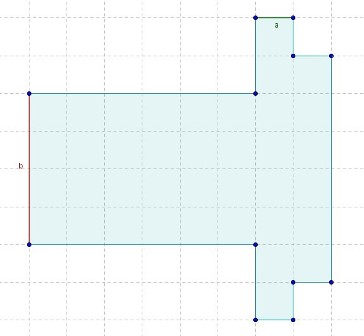
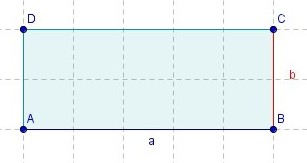
Setze nun für a=1cm und b=4cm ein
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Rezept
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
|
|
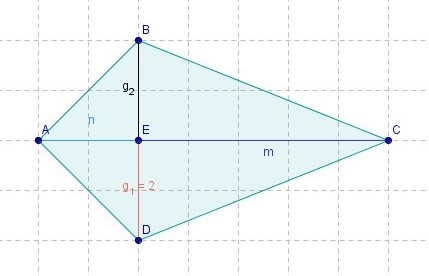
Interpretieren von Termen
|
|
Übungsaufgaben
a) Addiere 2 zum Quadrat von x
b) Addiere 6 zum vierfachen der Zahl n
c) Multipliziere die Summe aus b und der Zahl 7 mit 4
d) Multipliziere x mit seiner Gegenzahl
e) Multipliziere den Vorgänger der natürlichen Zahl n mit seinem Nachfolger
Warum gibt es meist zwei Möglichkeiten?
a) T(?)= 18
b) T(?)= 38
c) T(?)= 3
d) T(?)= 6
|
 einsetzbar ohne Verstoß gegen die Rechenregeln, bei der Berechnung eines Flächeninhalts ist es jedoch sinnvoll, nur positive Zahlen einzusetzen. Also
einsetzbar ohne Verstoß gegen die Rechenregeln, bei der Berechnung eines Flächeninhalts ist es jedoch sinnvoll, nur positive Zahlen einzusetzen. Also  =
=
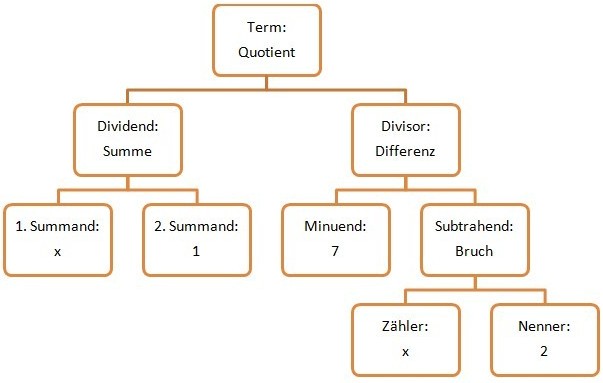
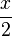 )
)
 ) = 5:(7-2) = 5:5 = 1
) = 5:(7-2) = 5:5 = 1

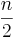 )+(4•
)+(4•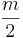 )
)

