Wikikurs-2-2010/Reitz Felix: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
'''Ich bin erfahrener Warcraft Spieler''' | '''Ich bin erfahrener Warcraft Spieler''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 59: | Zeile 36: | ||
(0) (0) (0) (!38) | (0) (0) (0) (!38) | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | <big>'''Aufgabe: (Es können auch mehrere Antworten richtig sein!)'''</big> | ||
| + | |||
| + | Was ergibt 34 + 91? | ||
| + | |||
| + | (125) (!115) (!135) (!38) | ||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | <big>'''Aufgabe: (Es können auch mehrere Antworten richtig sein!)'''</big> | ||
| + | |||
| + | Was ergibt <math>\frac{2}{4}+\frac{1}{3}</math>? | ||
| + | |||
| + | (!<math>\frac{5}{6}</math>) (!<math>\frac{3}{7}</math>) (1,2) (1) | ||
</div> | </div> | ||
Aktuelle Version vom 30. Juni 2010, 14:06 Uhr
Ich kann sehr gut Fußball spielen
Ich bin erfahrener Warcraft Spieler
Wer war der Weltfußballer 2009
Wie gut bist du in Mathe!
Aufgabe: (Es können auch mehrere Antworten richtig sein!)
Was ergibt 186 + 124?
(!2,2) (310) (!300) (!10000)
Aufgabe: (Es können auch mehrere Antworten richtig sein!)
Was ergibt 1 - 11?
(!2,2) (-10) (!-9) (!3)
Aufgabe: (Es können auch mehrere Antworten richtig sein!)
Was ergibt 19 + -19?
(0) (0) (0) (!38)
Aufgabe: (Es können auch mehrere Antworten richtig sein!)
Was ergibt 34 + 91?
(125) (!115) (!135) (!38)
Aufgabe: (Es können auch mehrere Antworten richtig sein!)
Was ergibt 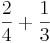 ?
?
(! ) (!
) (! ) (1,2) (1)
) (1,2) (1)

