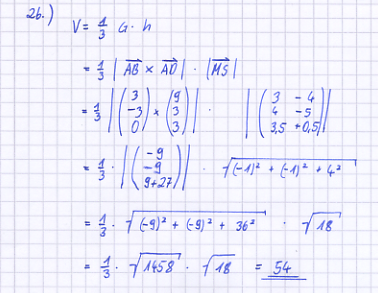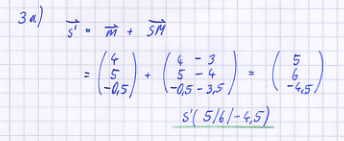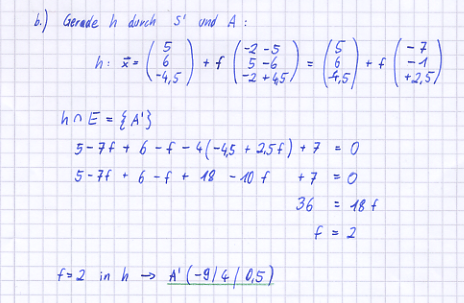2004 V: Unterschied zwischen den Versionen
(Andere /(Einfachere) Lösung zur Aufgabe 1c) in Popupkasten gesetzt) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 65: | Zeile 65: | ||
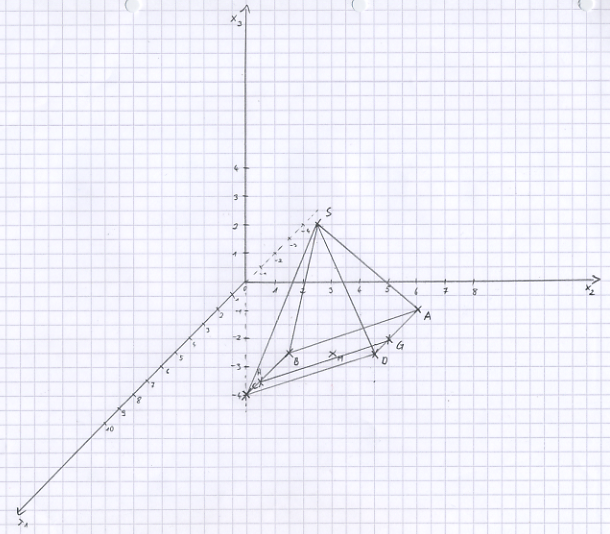
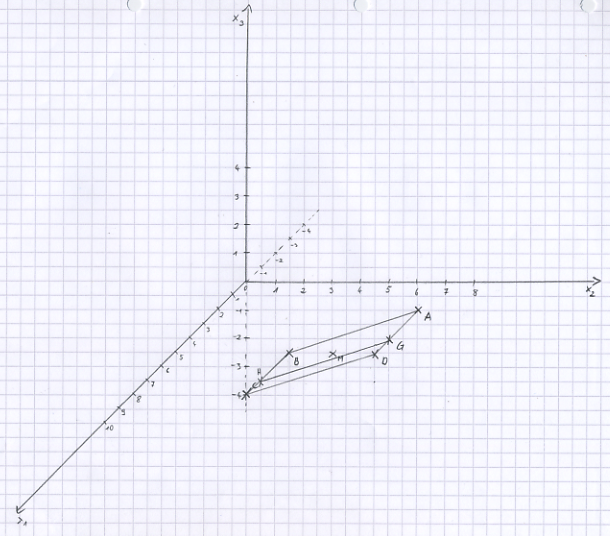
c) Die Parallelogrammfläche schneidet die x<sub>1</sub>x<sub>2</sub>-Ebene in der Strecke [GH]. Berechnen Sie die Koordinaten der Punkte der Punkte G und H und tragen Sie die Strecke [GH] in die angelegte Zeichnung ein. | c) Die Parallelogrammfläche schneidet die x<sub>1</sub>x<sub>2</sub>-Ebene in der Strecke [GH]. Berechnen Sie die Koordinaten der Punkte der Punkte G und H und tragen Sie die Strecke [GH] in die angelegte Zeichnung ein. | ||
| − | [Zur Kontrolle: (4|7|0) und (7|4|0)] | + | [Zur Kontrolle: (4|7|0) und (7|4|0)] |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:ABI_2004_V_1c_Lös.jpg|750px]] | + | [[Bild:ABI_2004_V_1c_Lös.jpg|750px]][[Bild:ABI_2004_V_1c2_Lös.jpg|750px]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Bild:ABI_2004_V_1c2_Lös.jpg|750px]] | + | |
}} | }} | ||
<popup name="Zeichnung"> | <popup name="Zeichnung"> | ||
| − | [[Bild:ABI_2004_V_1c_Zei.jpg|750px]] | + | [[Bild:ABI_2004_V_1c_Zei.jpg|750px]] |
</popup> | </popup> | ||
| + | <popup name="Andere Lösung"> | ||
| + | Die Punkte G und H liegen in Verlängerung der Parallelogrammseiten. Man stellt die Gerade durch A und B auf. <math> \vec a + \vec AB = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}</math> liefert keine Lösung, da die dritte Koordinate nicht Null werden kann. Analog dazu die Gerade durch C und D <math> \vec c + \vec CD = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}</math> | ||
| + | Das Gleiche macht man nun mit Gerade durch A und D <math> \vec a + \vec AD = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}</math> und erhält für x = 4 und für y = 7 <math>\Rightarrow \vec{p1} = \begin{pmatrix} 4 \\ 7 \\ 0 \end{pmatrix}</math>. Nun folgt die andere Gerade durch B und C <math> \vec b + \vec BC = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}</math>. Als Lösungen erhält man für x = 7 und für y = 4 <math>\Rightarrow \vec{p2} = \begin{pmatrix} 7 \\ 4 \\ 0 \end{pmatrix}</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <math> \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}</math> aus dem Grund, da bei allen Punkten in der x<sub>1,2</sub> Ebene, die z - Koordinate Null ist. x und y sind frei wählbar. Somit liegen alle Punkte, deren z = 0 ist, immer in der x<sub>1,2</sub> Ebene. | ||
| + | </popup> | ||
d) In welchem Verhältnis wird die Fläche des Parallelogramms durch die x<sub>1</sub>x<sub>2</sub>-Ebene geteilt? Begründen Sie Ihre Antwort. | d) In welchem Verhältnis wird die Fläche des Parallelogramms durch die x<sub>1</sub>x<sub>2</sub>-Ebene geteilt? Begründen Sie Ihre Antwort. | ||
Aktuelle Version vom 16. April 2010, 14:53 Uhr
|
|
|
E: x1 + x2 - 4 x3 + 7 = 0 gegeben.
|
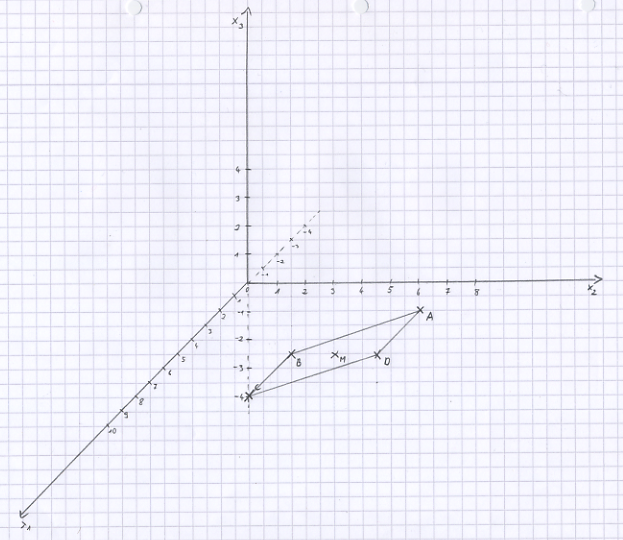
a) Bestimmen Sie die Koordinaten des Punktes D so, dass das Viereck ABCD ein Parallelogramm ist, und berechnen Sie die Koordinaten des Diagonalenschnittpunkts M. Legen Sie ein Koordinatensystem an (Querformat, Ursprung in Seitenmitte) und tragen Sie das Parallelogramm ABCD sowie den Punkt M ein. [Zur Kontrolle: M(4|5|-0,5)]
[Zur Kontrolle: (4|7|0) und (7|4|0)] d) In welchem Verhältnis wird die Fläche des Parallelogramms durch die x1x2-Ebene geteilt? Begründen Sie Ihre Antwort.
|
a) S ist der Punkt in E, der vom Diagonalenschnittpunkt M den geringsten Abstand hat. Berechnen Sie die Koordinaten von S und zeichnen Sie die Pyramide ABCDS in Ihre Zeichnung ein. [Zur Kontrolle: S(3|4|3,5)]
|
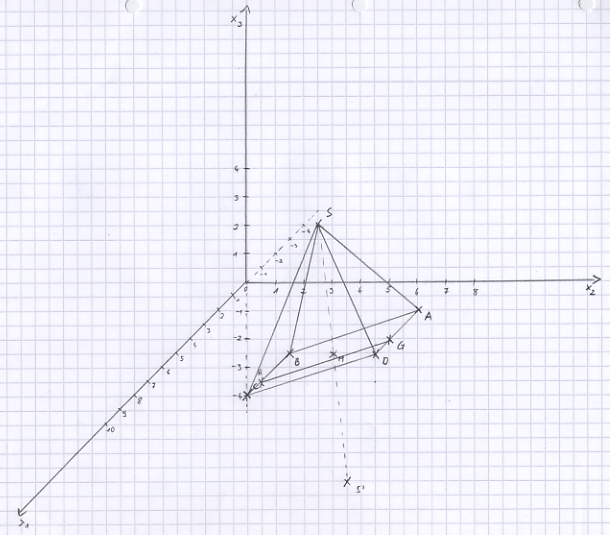
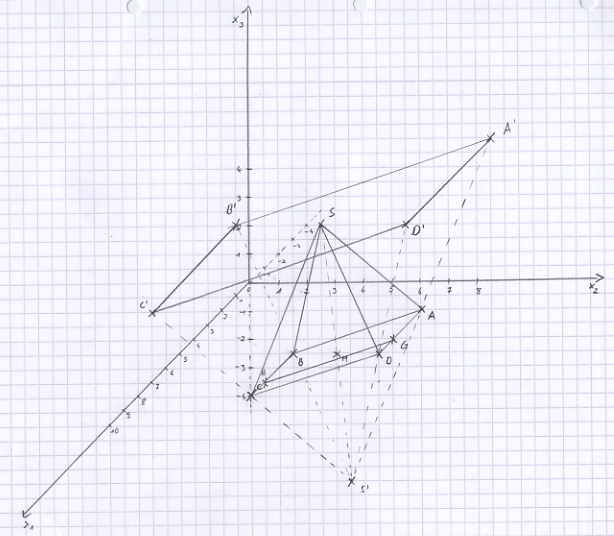
S' sei der Spiegelpunkt von S bezüglich der Ebene, in der das Parallelogramm ABCD liegt. a) Berechnen Sie die Koordinaten von S' und tragen Sie S' in die Zeichnung ein.
b) Berechnen Sie die Koordinaten des Bildpunktes A' von A. Tragen Sie ohne weitere Rechnung das Bildviereck A'B'C'D' in die Zeichnung ein
|
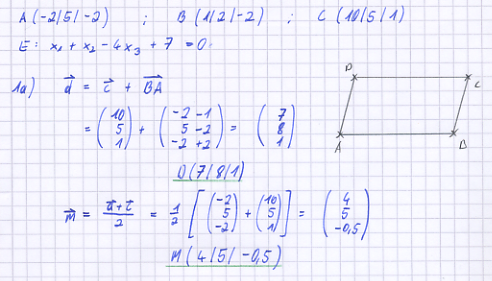
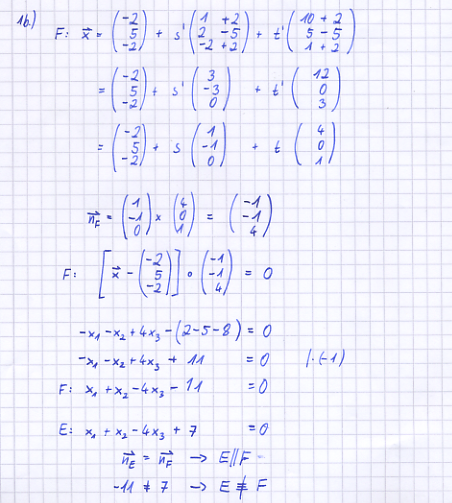
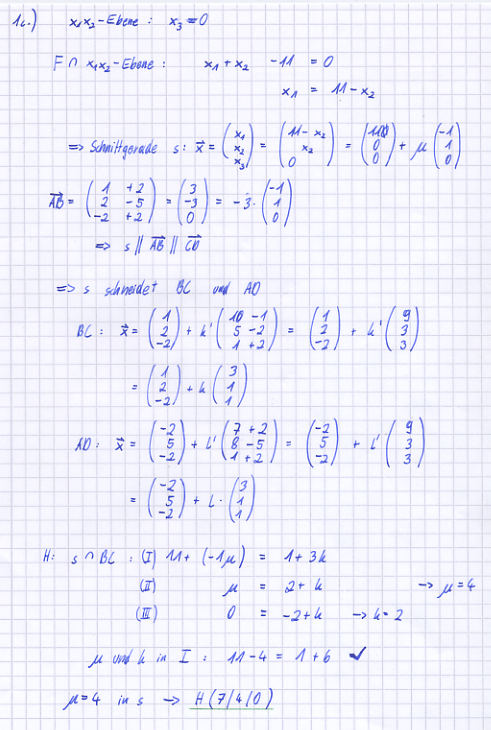

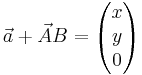 liefert keine Lösung, da die dritte Koordinate nicht Null werden kann. Analog dazu die Gerade durch C und D
liefert keine Lösung, da die dritte Koordinate nicht Null werden kann. Analog dazu die Gerade durch C und D 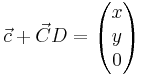
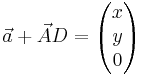 und erhält für x = 4 und für y = 7
und erhält für x = 4 und für y = 7 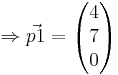 . Nun folgt die andere Gerade durch B und C
. Nun folgt die andere Gerade durch B und C 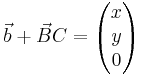 . Als Lösungen erhält man für x = 7 und für y = 4
. Als Lösungen erhält man für x = 7 und für y = 4 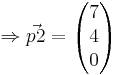 .
.
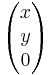 aus dem Grund, da bei allen Punkten in der x1,2 Ebene, die z - Koordinate Null ist. x und y sind frei wählbar. Somit liegen alle Punkte, deren z = 0 ist, immer in der x1,2 Ebene.
aus dem Grund, da bei allen Punkten in der x1,2 Ebene, die z - Koordinate Null ist. x und y sind frei wählbar. Somit liegen alle Punkte, deren z = 0 ist, immer in der x1,2 Ebene.