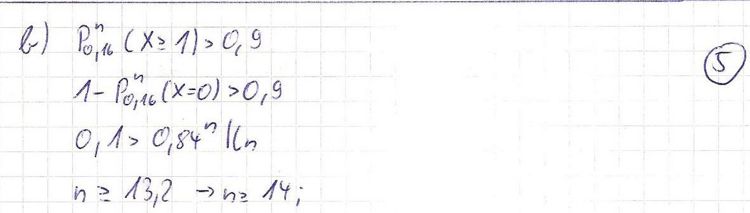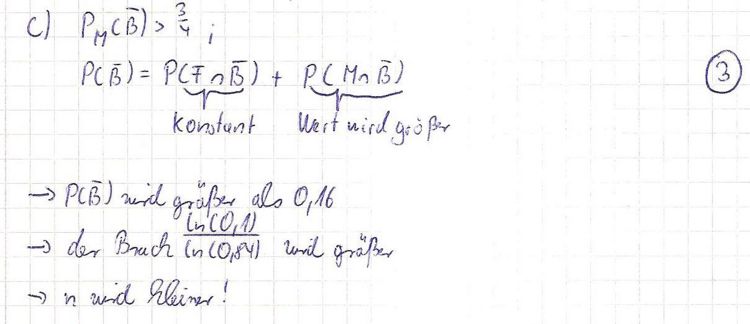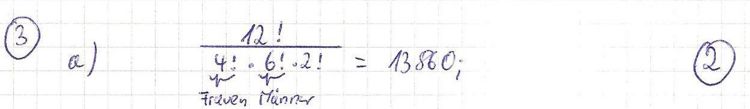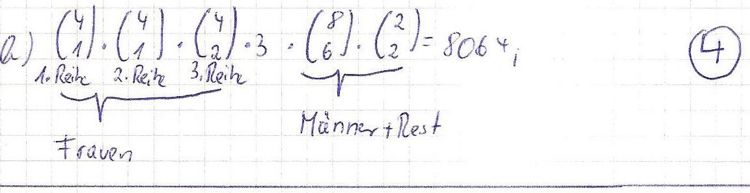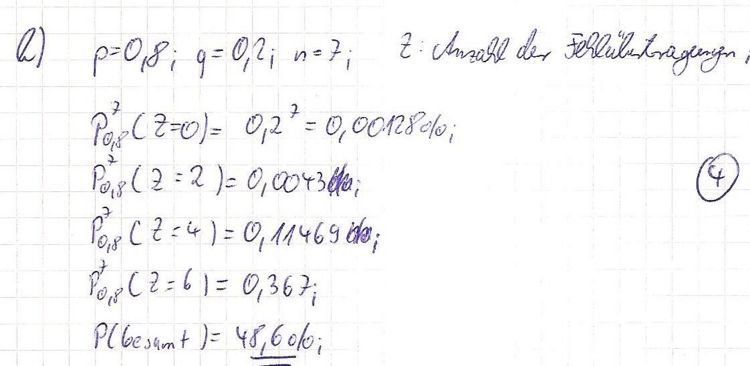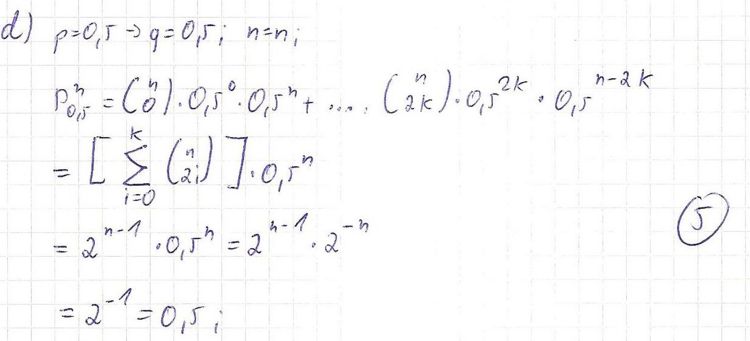2003 III: Unterschied zwischen den Versionen
K |
|||
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2003'''</big></center> | |
| + | <center><big>'''Stochastik III'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6'''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:abituraufgabe2003stochastikIIIlösung.doc|Lösung gesamt]]</center> | ||
| + | |||
| + | |||
| + | <center>'''Erarbeitet von Philipp Ißle, Michael Scheller, Sebastian Schirmer'''</center> | ||
| + | |||
| + | |||
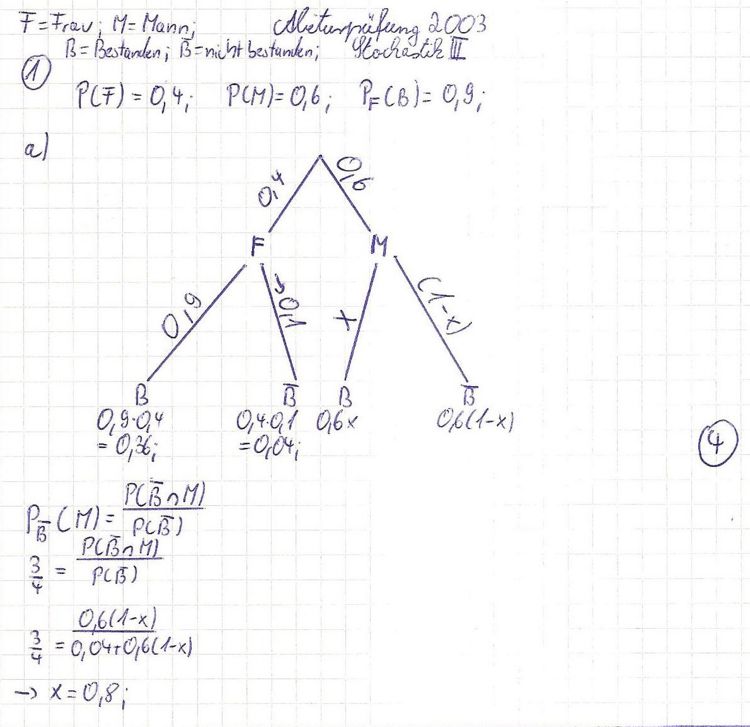
| + | 1. Bei einem Einstellungstermin für den Polizeidienst waren 40 % der Bewerber Frauen, von denen 90 % die Aufnahmeprüfung bestanden. Drei Viertel derjenigen, die scheiterten, waren männlich. | ||
| + | |||
| + | a) Welcher Anteil der männlichen Teilnehmer hat die Aufnahmeprüfung bestanden? [Ergebnis: 80 %] '''4BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III1a.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | b) Wie viele unter einer größeren Zahl von zufällig ausgewählten Prüfungsarbeiten müssen mindestens korrigiert werden, damit mit einer Wahrscheinlichkeit von mehr als 90 % wenigstens eine darunter ist, welche als nicht bestanden bewertet wird? Rechnen Sie wie bei „Ziehen mit Zurücklegen“. '''5BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III1b.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | c) Wie verändert sich das Ergebnis aus Teilaufgabe 1b, wenn nicht drei Viertel der Teilnehmer, die scheitern, männlich sind, sondern ein deutlich höherer Anteil, und die sonstigen Ausgangsbedingungen unverändert bleiben? Begründen Sie Ihre Antwort. '''3BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III1c.jpeg|750px]] | ||
| + | }} | ||
| + | 2. Bei einem Einstellungstermin stehen 750 Polizeianwärterstellen zur Verfügung. Erfahrungsgemäß scheitern 16 % der Bewerber bei der Aufnahmeprüfung. Mit welcher Wahrscheinlichkeit können bei 880 Bewerbern nicht alle, die die Prüfung bestehen, übernommen werden? Verwenden Sie die Normalverteilung als Näherung. '''4BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III2.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | 3. Für die EDV-Ausbildung einer Gruppe von 4 weiblichen und 6 männlichen Polizeianwärtern steht ein Schulungsraum mit 12 Computerarbeitsplätzen zur Verfügung. | ||
| + | |||
| + | |||
| + | a) Auf wie viele verschiedene Arten kann sich die Gruppe auf die Arbeitsplätze verteilen, wenn nur nach dem Geschlecht unterschieden wird? '''2BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III3a.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | b) Die Arbeitsplätze sind in 3 Reihen zu je 4 Plätzen angeordnet. Auf wie viele verschiedene Arten können die Anwärter Platz nehmen, | ||
| + | wenn in jeder Reihe mindestens eine Polizeianwärterin sitzen soll und wiederum nur nach dem Geschlecht unterschieden wird? '''4BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III3b.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | 4. Die Polizeianwärter sollen üben, Nachrichten an andere Dienststellen weiterzuleiten. Dazu soll die Nachricht „Die beiden Fingerabdrücke stimmen überein“ von einem Computer zum nächsten und so fort übermittelt werden. Durch einen bewusst eingebauten Übertragungsfehler wird die Meldung bei jeder einzelnen Übermittlung mit einer Wahrscheinlichkeit p in ihr Gegenteil verkehrt; andere Übertragungsfehler treten nicht auf. | ||
| + | |||
| + | a) Berechnen Sie in Abhängigkeit von p die Wahrscheinlichkeit dafür, dass in einer Kette aus 4 Übermittlungen der Übertragungsfehler genau zweimal auftritt und die Nachricht somit wieder richtig ankommt. Berechnen Sie den größten Wert, den diese Wahrscheinlichkeit annehmen kann. '''6BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III4a.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | b) Wie groß ist für p = 0,8 die Wahrscheinlichkeit dafür, dass die Nachricht bei einer Kette von 7 Übertragungen am Ende richtig ankommt? '''4BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III4b.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | c) Es gilt die Beziehung:<math>\sum_{i=0}^{k}{n \choose 2i}= 2</math><sup>n-1</sup> wobei k die größte ganze Zahl kleiner oder gleich <math>\frac{n}{2}</math> ist. | ||
| + | Bestätigen Sie die Gültigkeit der Beziehung für n = 6 und n = 7 durch Einsetzen. '''3BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III4c.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | d) Zeigen Sie allgemein, dass die Wahrscheinlichkeit dafür, dass für p = 0,5 bei einer Kette beliebiger Länge die Nachricht richtig ankommt, stets 0,5 beträgt. Die allgemein gültige Beziehung aus Teilaufgabe 4c darf verwendet werden. '''5BE''' | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:abituraufgabe2003III4d.jpeg|750px]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | --[[Benutzer:Philipp.Issle|Issi]] 06:12, 24. Apr. 2010 (UTC) | ||
Aktuelle Version vom 24. April 2010, 07:15 Uhr
1. Bei einem Einstellungstermin für den Polizeidienst waren 40 % der Bewerber Frauen, von denen 90 % die Aufnahmeprüfung bestanden. Drei Viertel derjenigen, die scheiterten, waren männlich.
a) Welcher Anteil der männlichen Teilnehmer hat die Aufnahmeprüfung bestanden? [Ergebnis: 80 %] 4BE
b) Wie viele unter einer größeren Zahl von zufällig ausgewählten Prüfungsarbeiten müssen mindestens korrigiert werden, damit mit einer Wahrscheinlichkeit von mehr als 90 % wenigstens eine darunter ist, welche als nicht bestanden bewertet wird? Rechnen Sie wie bei „Ziehen mit Zurücklegen“. 5BE
c) Wie verändert sich das Ergebnis aus Teilaufgabe 1b, wenn nicht drei Viertel der Teilnehmer, die scheitern, männlich sind, sondern ein deutlich höherer Anteil, und die sonstigen Ausgangsbedingungen unverändert bleiben? Begründen Sie Ihre Antwort. 3BE
2. Bei einem Einstellungstermin stehen 750 Polizeianwärterstellen zur Verfügung. Erfahrungsgemäß scheitern 16 % der Bewerber bei der Aufnahmeprüfung. Mit welcher Wahrscheinlichkeit können bei 880 Bewerbern nicht alle, die die Prüfung bestehen, übernommen werden? Verwenden Sie die Normalverteilung als Näherung. 4BE
3. Für die EDV-Ausbildung einer Gruppe von 4 weiblichen und 6 männlichen Polizeianwärtern steht ein Schulungsraum mit 12 Computerarbeitsplätzen zur Verfügung.
a) Auf wie viele verschiedene Arten kann sich die Gruppe auf die Arbeitsplätze verteilen, wenn nur nach dem Geschlecht unterschieden wird? 2BE
b) Die Arbeitsplätze sind in 3 Reihen zu je 4 Plätzen angeordnet. Auf wie viele verschiedene Arten können die Anwärter Platz nehmen, wenn in jeder Reihe mindestens eine Polizeianwärterin sitzen soll und wiederum nur nach dem Geschlecht unterschieden wird? 4BE
4. Die Polizeianwärter sollen üben, Nachrichten an andere Dienststellen weiterzuleiten. Dazu soll die Nachricht „Die beiden Fingerabdrücke stimmen überein“ von einem Computer zum nächsten und so fort übermittelt werden. Durch einen bewusst eingebauten Übertragungsfehler wird die Meldung bei jeder einzelnen Übermittlung mit einer Wahrscheinlichkeit p in ihr Gegenteil verkehrt; andere Übertragungsfehler treten nicht auf.
a) Berechnen Sie in Abhängigkeit von p die Wahrscheinlichkeit dafür, dass in einer Kette aus 4 Übermittlungen der Übertragungsfehler genau zweimal auftritt und die Nachricht somit wieder richtig ankommt. Berechnen Sie den größten Wert, den diese Wahrscheinlichkeit annehmen kann. 6BE
b) Wie groß ist für p = 0,8 die Wahrscheinlichkeit dafür, dass die Nachricht bei einer Kette von 7 Übertragungen am Ende richtig ankommt? 4BE
c) Es gilt die Beziehung: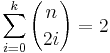
n-1 wobei k die größte ganze Zahl kleiner oder gleich 
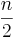ist.
Bestätigen Sie die Gültigkeit der Beziehung für n = 6 und n = 7 durch Einsetzen. 3BE
d) Zeigen Sie allgemein, dass die Wahrscheinlichkeit dafür, dass für p = 0,5 bei einer Kette beliebiger Länge die Nachricht richtig ankommt, stets 0,5 beträgt. Die allgemein gültige Beziehung aus Teilaufgabe 4c darf verwendet werden. 5BE
--Issi 06:12, 24. Apr. 2010 (UTC)
