2004 II: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Isabell, Ann Christin, Johanna) |
(Verbesserung 1a hinzugefügt) |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | |
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2004'''</big></center> | ||
| + | <center><big>'''Infinitesimalrechnung II'''</big></center> | ||
| + | |||
| + | |||
| + | <center> [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=3b6f5b35e5627e5c952006db5cc4aa9d'''Download der Originalaufgaben: Abitur 2004 LK Mathematik Bayern'''] | ||
| + | |||
| + | |||
| + | |||
| + | Erarbeitet von Johanna Buchner, Isabell Geist und Ann Christin Werner</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
| + | |||
| + | Gegeben ist die Schar der Funktionen <math>f_{k}:x = \frac{x^2}{1-kx^2} </math> mit der maximalen Definitionsmenge D<sub>k</sub> und k <math>\in </math> IR. G<sub>k</sub> bezeichnet den Graphen von f<sub>k</sub>. | ||
| + | |||
| + | |||
| + | |||
| + | a) Bestimmen Sie für k < 0 und k > 0 jeweils die Definitionsmenge D<sub>k</sub>. Untersuchen Sie für k <math>\neq </math> 0 das Verhalten von f<sub>k</sub> für <math>x \to \infty</math> und <math>x \to -\infty</math>. Geben Sie die Gleichungen aller Asymptoten an. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Werner_Ann_Christin_Abitur2004_InfiniIIa.jpg]]<br /> | ||
| + | '''Kleine Verbesserung:'''<br /> | ||
| + | In der letzten Zeile muss es statt y=... x=+/-<math>\sqrt{1/k}</math> heißen, da diejenigen Stellen beschrieben werden, an denen senkrechte Asymptoten auftreten. | ||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | |||
| + | |||
| + | b) Zeigen Sie, dass gilt: <math>f'_{k} (x) = \frac{2x}{\left(1 - kx^2\right)^2 } </math>. | ||
| + | |||
| + | |||
| + | Begründen Sie, dass alle Graphen G<sub>k</sub> einen gemeinsamen Tiefpunkt besitzen. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Werner_Ann_Christin_Abitur2004_InfiniIIb.jpg]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | |||
| + | |||
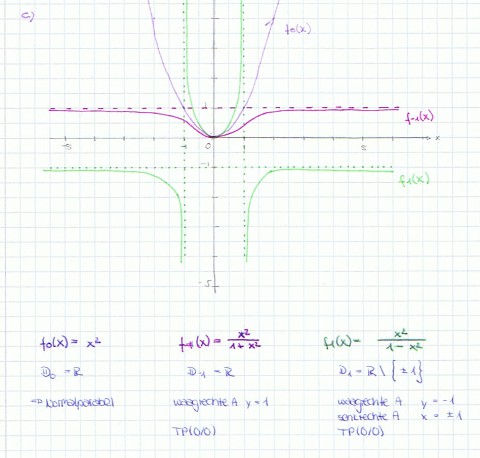
| + | c) Skizzieren Sie G<sub>-1</sub> und G<sub>1</sub> in ein gemeinsames Koordinatensystem. Zeichnen Sie auch alle vorhandenen Asymptoten ein. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abiaufgabe2004_Infini23.jpg]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''7 BE'''</i></div> | ||
| + | |||
| + | |||
| + | d) Beschreiben Sie für den Fall k < 0, wie sich die Lage der waagerechten Asymptote von G<sub>k</sub> für <math>k \to -\infty</math> und <math>k \to 0</math> jeweils verändert. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abiaufgabe2004_Infini24.jpg]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | |||
| + | |||
| + | e) Bestimmen Sie k zunächst so, dass G<sub>k</sub> durch den Punkt P (1|2) verläuft. | ||
| + | |||
| + | Zeigen Sie dann, dass durch jeden beliebigen Punkt, der nicht auf einer der Koordinatenachsen liegt, genau ein Graph G<sub>k</sub> verläuft. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abiaufgabe2004_Infini25.jpg]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
| + | |||
| + | Das nebenstehende Diagramm zeigt, wie die Geschwindigkeit eines Fahrzeugs von der Zeit abhängt; der zugehörige Funktionsterm für 0 <math>\leq </math> t <math>\leq </math> 10 ist <math>v (t) = 7t * e^{-0,1t} </math>. | ||
| + | |||
| + | Dabei bezeichnet v die Maßzahl der in Metern pro Sekunde gemessenen Geschwindigkeit, t die Maßzahl der in Sekunden gemessenen Zeit. | ||
| + | |||
| + | Der Inhalt der Fläche zwischen dem Graphen, der t-Achse und der Geraden t = t<sub>0</sub> entspricht dem während der ersten t<sub>0</sub> Sekunden zurückgelegten Weg (in Metern). | ||
| + | |||
| + | |||
| + | a) Berechnen Sie den Weg, den das Fahrzeug in den ersten 10 Sekunden zurücklegt. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abiaufgabe2004_Infini26.jpg]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''8 BE'''</i></div> | ||
| + | |||
| + | |||
| + | Ab dem Zeitpunkt t = 10 wird das Fahrzeug bis zum Stillstand abgebremst. Dabei wird die Abhängigkeit der Geschwindigkeit von der Zeit durch eine lineare Funktion beschrieben. | ||
| + | |||
| + | |||
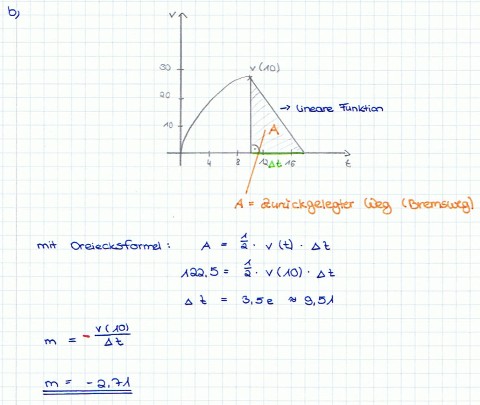
| + | b) Ermitteln Sie die Steigung dieser linearen Funktion, wenn der Bremsweg 122,5 Meter beträgt. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abiaufgabe2004_Infini27.jpg]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 15. April 2010, 16:33 Uhr
|
|
Gegeben ist die Schar der Funktionen
a) Bestimmen Sie für k < 0 und k > 0 jeweils die Definitionsmenge Dk. Untersuchen Sie für k
In der letzten Zeile muss es statt y=... x=+/-
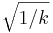 heißen, da diejenigen Stellen beschrieben werden, an denen senkrechte Asymptoten auftreten. heißen, da diejenigen Stellen beschrieben werden, an denen senkrechte Asymptoten auftreten.6 BE
5 BE
7 BE
3 BE
Zeigen Sie dann, dass durch jeden beliebigen Punkt, der nicht auf einer der Koordinatenachsen liegt, genau ein Graph Gk verläuft.
6 BE
|
Das nebenstehende Diagramm zeigt, wie die Geschwindigkeit eines Fahrzeugs von der Zeit abhängt; der zugehörige Funktionsterm für 0 Dabei bezeichnet v die Maßzahl der in Metern pro Sekunde gemessenen Geschwindigkeit, t die Maßzahl der in Sekunden gemessenen Zeit. Der Inhalt der Fläche zwischen dem Graphen, der t-Achse und der Geraden t = t0 entspricht dem während der ersten t0 Sekunden zurückgelegten Weg (in Metern).
8 BE
5 BE
|
 mit der maximalen Definitionsmenge Dk und k
mit der maximalen Definitionsmenge Dk und k  IR. Gk bezeichnet den Graphen von fk.
IR. Gk bezeichnet den Graphen von fk.
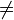 0 das Verhalten von fk für
0 das Verhalten von fk für 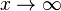 und
und 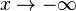 . Geben Sie die Gleichungen aller Asymptoten an.
. Geben Sie die Gleichungen aller Asymptoten an.

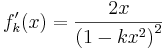 .
.

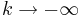 und
und 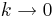 jeweils verändert.
jeweils verändert.


 t
t 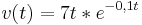 .
.