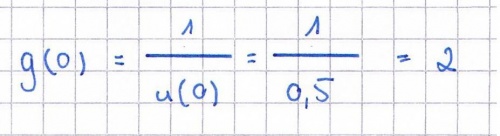2005 II: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(Aufgabe 1e Lösung anzeigen zweimal entfernt) |
(Bemerkungen verändert) |
||
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 96: | Zeile 96: | ||
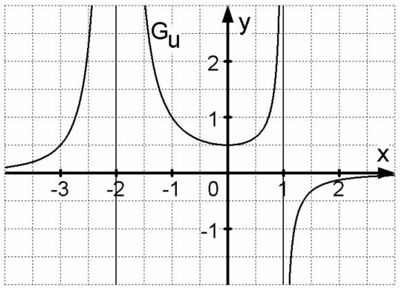
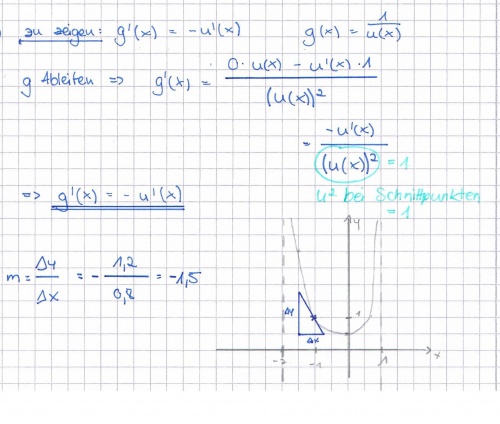
c) Zeigen Sie, dass für alle Schnittpunkte von G<sub>u</sub> und G<sub>g</sub> gilt: g' (x)= -u' (x). Ermitteln Sie g' (-1), indem Sie u' (-1) möglichst genau aus obiger Abbildung ablesen. (Entsprechende Hilfslinien sind einzuzeichnen.)<div align="right">''5 BE''</div> | c) Zeigen Sie, dass für alle Schnittpunkte von G<sub>u</sub> und G<sub>g</sub> gilt: g' (x)= -u' (x). Ermitteln Sie g' (-1), indem Sie u' (-1) möglichst genau aus obiger Abbildung ablesen. (Entsprechende Hilfslinien sind einzuzeichnen.)<div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt|1=[[Bild: | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_2c_Lös.jpg|500px]]}} |
d) Geben Sie g(0) an. Skizzieren Sie in obige Abbildung unter Berück-sichtigung der gewonnenen Ergebnisse einen möglichen Graphen G<sub>g</sub>.<div align="right">''3 BE''</div> | d) Geben Sie g(0) an. Skizzieren Sie in obige Abbildung unter Berück-sichtigung der gewonnenen Ergebnisse einen möglichen Graphen G<sub>g</sub>.<div align="right">''3 BE''</div> | ||
| − | :{{Lösung versteckt|1=[[Bild: | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_2d_Lös.jpg|500px]]}} |
Aktuelle Version vom 30. März 2010, 10:57 Uhr
|
|
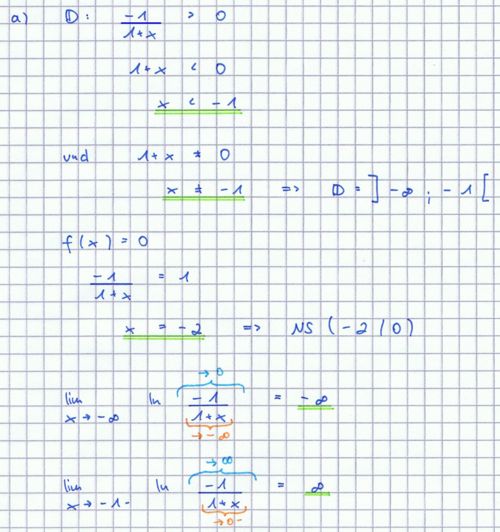
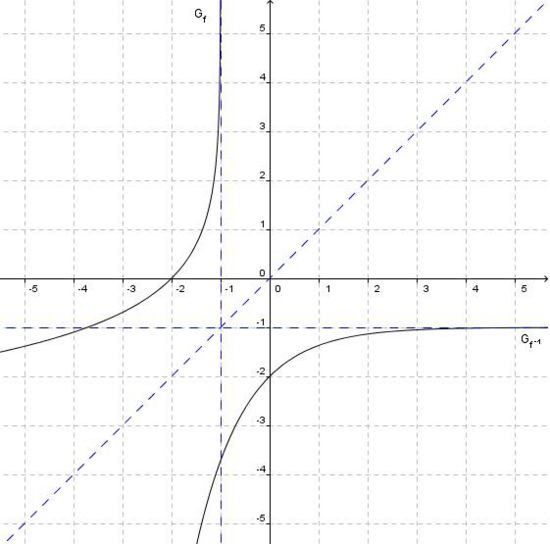
Gegeben ist die Funktion
4 BE
4 BE
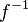 an und ermitteln Sie den Funktionsterm an und ermitteln Sie den Funktionsterm 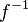 (x). (x).5 BE
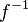 in ein Koordinatensystem. Tragen Sie dazu auch alle Asymptoten sowie die Schnittpunkte mit den Koordinatenachsen ein. in ein Koordinatensystem. Tragen Sie dazu auch alle Asymptoten sowie die Schnittpunkte mit den Koordinatenachsen ein.5 BE
4 BE
1. Lösung (einfacher) 2. Lösung (zeitaufwändiger und komplizierter)
|
Es sei g eine in IR differenzierbare Funktion mit dem Graphen Gg. Die Abbildung zeigt den Graphen Gu der in IR\{-2;1} definierten Funktion
5 BE
5 BE
5 BE
3 BE
|
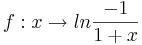 mit dem maximal möglichen Definitionsbereich D. Der Graph von f wird mit Gf bezeichnet.
mit dem maximal möglichen Definitionsbereich D. Der Graph von f wird mit Gf bezeichnet.



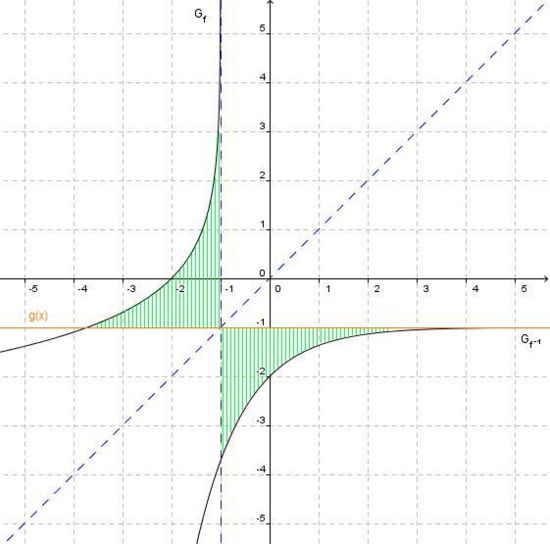

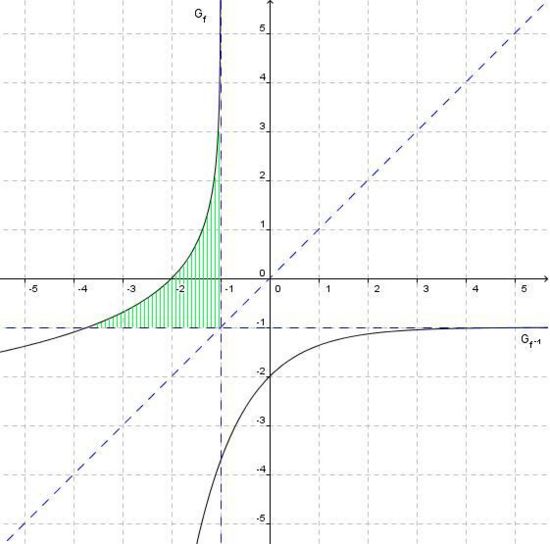
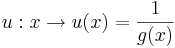 . Die x-Achse und die Geraden x= –2 und x=1 sind Asymptoten von Gu.
. Die x-Achse und die Geraden x= –2 und x=1 sind Asymptoten von Gu.