2004 I: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
K (abi_2004) |
(Verbesserung 3c hinzugefügt) |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
<center><big>'''Infinitestimalrechnung I'''</big></center> | <center><big>'''Infinitestimalrechnung I'''</big></center> | ||
| + | [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=3b6f5b35e5627e5c952006db5cc4aa9d'''Download der Originalaufgaben: Abitur 2005 LK Mathematik Bayern'''] | ||
| + | <br><br>[[Media:gesamt_2004_abi.doc|gesamte Lösung]] | ||
| + | <br><br>Ruth, Vroni, Julian | ||
| Zeile 22: | Zeile 25: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| + | <div align="left"> | ||
| + | Gegeben ist die in IR definierte Funktion f mit <math>f_k:x\rightarrow 10(e^{-0,5x}-e^{-x})</math>. | ||
| + | Der zugehörige Graph ist nebenstehend skizziert. <br><br><br> | ||
| + | [[Bild:grafik_2004_abi.jpg]] | ||
| − | + | ;Aufgabe 1. | |
| − | + | Untersuchen Sie durch Rechnung | |
| + | a) das Verhalten von <math>f\,</math> für <math>x \rightarrow +\infty</math> und <math>x \rightarrow -\infty</math> | ||
| + | <div align="right">3BE</div> | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi_2004_1_a.jpg|750px]] | ||
| + | }} | ||
| − | |||
| − | |||
b) in welchen Intervallen die Funktionswerte von f positiv bzw. negativ sind, | b) in welchen Intervallen die Funktionswerte von f positiv bzw. negativ sind, | ||
| − | + | <div align="right">4BE</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_1_b.jpg|750px]] |
}} | }} | ||
| − | + | c) Lage und Art des Extrempunkts des Graphen von f. [Zur Kontrolle: H(2ln2/2.5)] | |
| − | + | <div align="right">6BE</div> | |
| − | + | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_1_c.jpg|750px]] |
}} | }} | ||
| − | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_1_c_2.jpg|750px]] |
}} | }} | ||
| Zeile 52: | Zeile 56: | ||
Einem Patienten wird zum Zeitpunkt x=0 eine bestimmte Menge eines Medikamentes verabreicht. | Einem Patienten wird zum Zeitpunkt x=0 eine bestimmte Menge eines Medikamentes verabreicht. | ||
Der obige Term f(x) beschreibt die Konzentration dieses Medikaments (Anzahl der Milliliter pro Liter Blut) nach x Stunden. <br>Berechnen sie den Zeitpunkt, zu dem die Konzentration auf 75% ihres Höchstwerts abgesunken ist. | Der obige Term f(x) beschreibt die Konzentration dieses Medikaments (Anzahl der Milliliter pro Liter Blut) nach x Stunden. <br>Berechnen sie den Zeitpunkt, zu dem die Konzentration auf 75% ihres Höchstwerts abgesunken ist. | ||
| − | + | <div align="right">7BE</div> | |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_2_a.jpg|750px]] |
}} | }} | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| − | Nun werden die in IR definierten Integralfunktionen | + | Nun werden die in IR definierten Integralfunktionen <math>F a(x)=\int_{a}^{x} f (t)\,dt</math>, a ∈ IR. betrachtet. |
| + | Der Graph vob F<sub>a </sub> wird mit G<sub>a</sub> bezeichnet. | ||
| + | |||
| + | ;a) | ||
| + | Bestimmen Sie das Monotonie- und das Krümmungsverhalten von G<sub>a</sub> ohne Ausführung der Integration (kurze Begründung). | ||
| + | <div align="right">4BE</div> | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi_2004_3_a.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | ;b) | ||
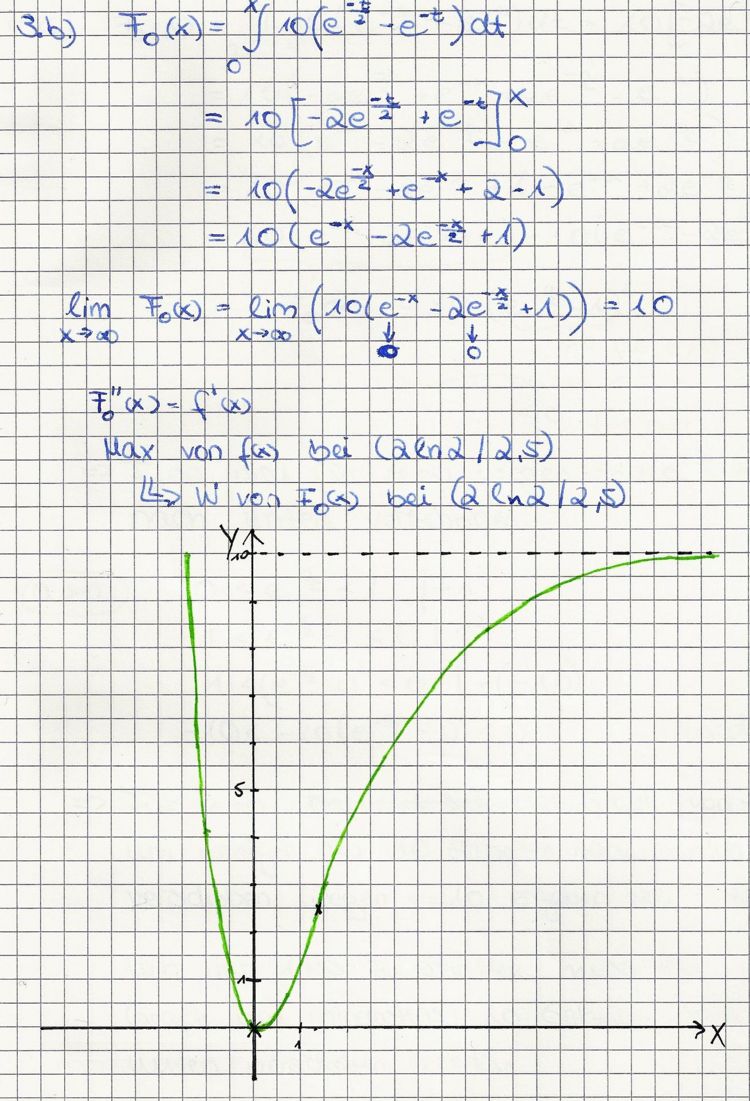
| + | Bestimmen Sie eine integralfreie Darstellung von F<sub>0</sub>(x) und zeigen Sie, dass gilt: | ||
| + | <math>\lim_{x \to \infty} \ </math> F<sub>0</sub> (x) = 10 | ||
| + | <div align="right">9BE</div> | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi_2004_3_b.jpg|750px]] | ||
| + | }} | ||
| + | Berechnen Sie die Koordinaten des Wendepunkts von G<sub>0</sub>. | ||
| + | Skizzieren Sie G<sub>0</sub> unter Verwendung der bisherigen Ergebnisse. | ||
| + | |||
| + | ;c) | ||
| + | Erklären Sie, warum jede Funktion F<sub>a</sub> mit a>0 genau zwei Nullstellen hat. | ||
| + | (explizite Berechnung der Nullstellen nicht verlangt) | ||
| + | Erläutern Sie, warum es Funktionen F<sub>a</sub> mit a<0 gibt, die genau eine Nullstelle haben. | ||
| + | <div align="right">7BE</div> | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Abi_2004_3_c.jpg|750px]]<br /> | ||
| + | '''Kleine Verbesserung:'''<br /> | ||
| + | Bei a>0 muss die 3. Zeile statt <math>1<(e^{-a/2}-1)^2<0</math> wie folgt heißen, da ja 1 nicht kleiner als 0 sein kann:<br /> | ||
| + | <math>1>(e^{-a/2}-1)^2>0</math> .<br /> | ||
| + | Die 4. Zeile stimmt dann wieder, da durch die Multiplikation mit (-10) ein Zeichenwechsel erfolgen muss. | ||
| + | }} | ||
| + | </div> | ||
Aktuelle Version vom 15. April 2010, 16:11 Uhr
|
Download der Originalaufgaben: Abitur 2005 LK Mathematik Bayern
|
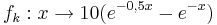 .
Der zugehörige Graph ist nebenstehend skizziert.
.
Der zugehörige Graph ist nebenstehend skizziert. 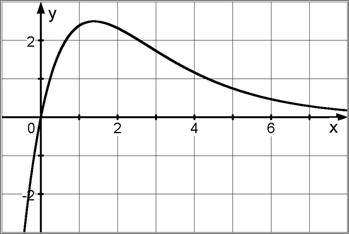
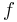 für
für 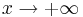 und
und 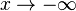
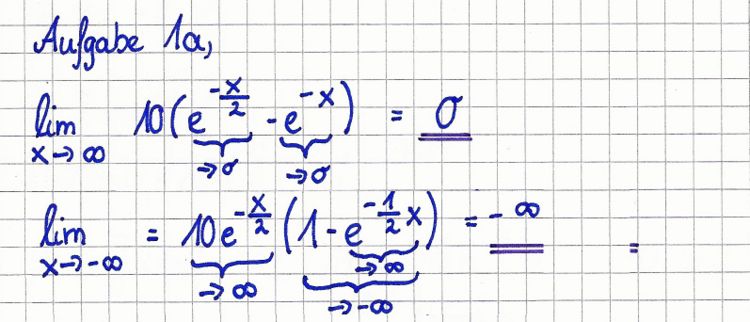
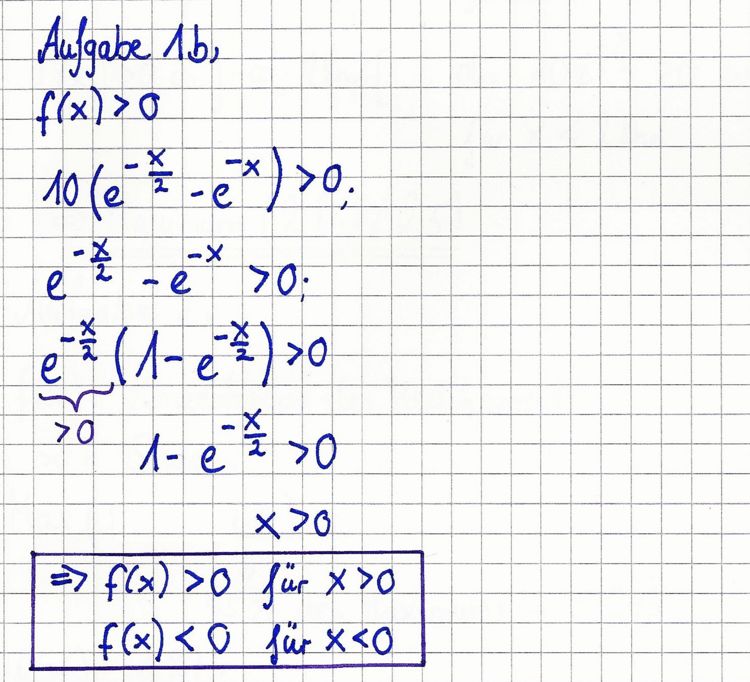
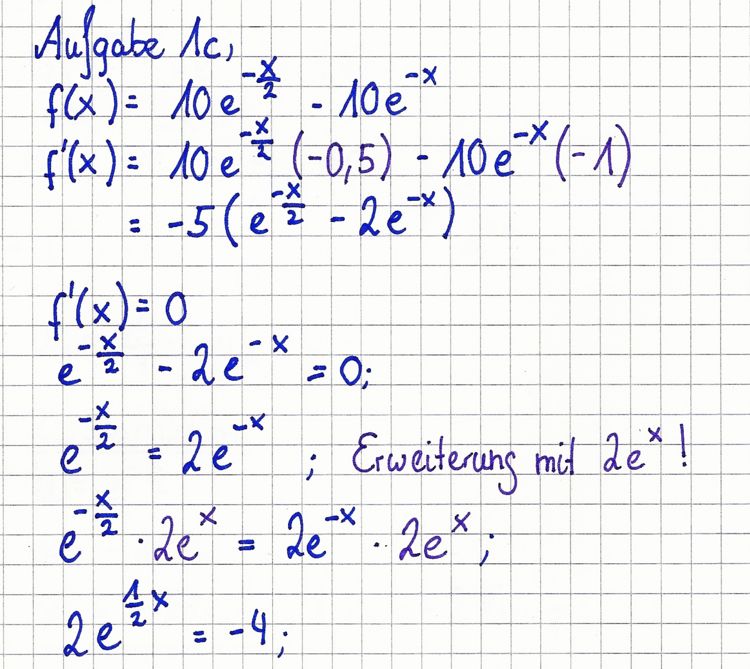


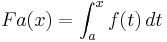 , a ∈ IR. betrachtet.
Der Graph vob Fa wird mit Ga bezeichnet.
, a ∈ IR. betrachtet.
Der Graph vob Fa wird mit Ga bezeichnet.

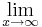 F0 (x) = 10
F0 (x) = 10

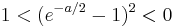 wie folgt heißen, da ja 1 nicht kleiner als 0 sein kann:
wie folgt heißen, da ja 1 nicht kleiner als 0 sein kann: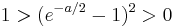 .
.
