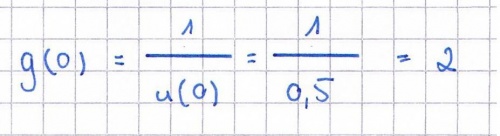2005 II: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(komplette Angabe ohne Lösungen) |
(Bemerkungen verändert) |
||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID= | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=41250891258e7bfb9e5538af466f1380'''Download der Originalaufgaben: Abitur 2005 LK Mathematik Bayern'''] - [[Media:LKM Abi 2005 II lös.doc|Lösungen zum Ausdrucken]] |
<br> | <br> | ||
Lösungen erstellt von: Sara Schirmer und Melissa Gehrig</center> | Lösungen erstellt von: Sara Schirmer und Melissa Gehrig</center> | ||
| Zeile 27: | Zeile 27: | ||
Gegeben ist die Funktion <math>f:x \rightarrow ln {-1 \over 1+x} </math> mit dem maximal möglichen Definitionsbereich D. Der Graph von f wird mit G<sub>f</sub> bezeichnet. | Gegeben ist die Funktion <math>f:x \rightarrow ln {-1 \over 1+x} </math> mit dem maximal möglichen Definitionsbereich D. Der Graph von f wird mit G<sub>f</sub> bezeichnet. | ||
| − | |||
| − | |||
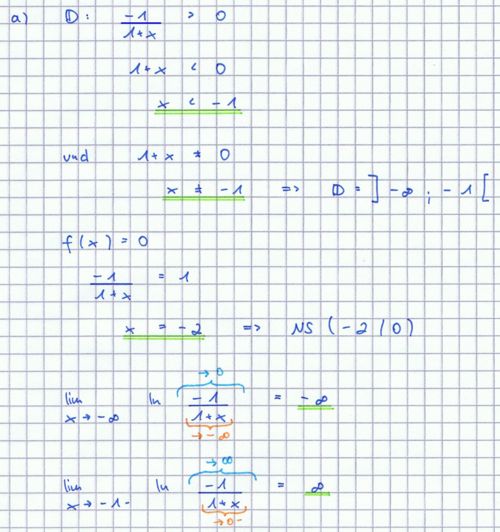
a) Bestimmen Sie D, die Nullstelle von f sowie das Verhalten von f an den Rändern von D.<div align="right">''4 BE''</div> | a) Bestimmen Sie D, die Nullstelle von f sowie das Verhalten von f an den Rändern von D.<div align="right">''4 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_1a_Lös.jpg|500px]]}} |
| − | + | ||
| − | [[Bild:ABI_2005_II_1a_Lös.jpg|500px]] | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
b) Untersuchen Sie das Monotonieverhalten von f.<div align="right">''4 BE''</div> | b) Untersuchen Sie das Monotonieverhalten von f.<div align="right">''4 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_1b_Lös.jpg|550px]]}} |
| − | + | ||
| − | [[Bild:ABI_2005_II_1b_Lös.jpg| | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
c) Warum besitzt f eine Umkehrfunktion? Geben Sie die Definitionsmenge der Umkehrfunktion <math>f^{-1}</math> an und ermitteln Sie den Funktionsterm <math>f^ {-1}</math>(x).<div align="right">''5 BE''</div> | c) Warum besitzt f eine Umkehrfunktion? Geben Sie die Definitionsmenge der Umkehrfunktion <math>f^{-1}</math> an und ermitteln Sie den Funktionsterm <math>f^ {-1}</math>(x).<div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_1c_Lös.jpg|550px]]}} |
| − | + | ||
| − | [[Bild:ABI_2005_II_1c_Lös.jpg| | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
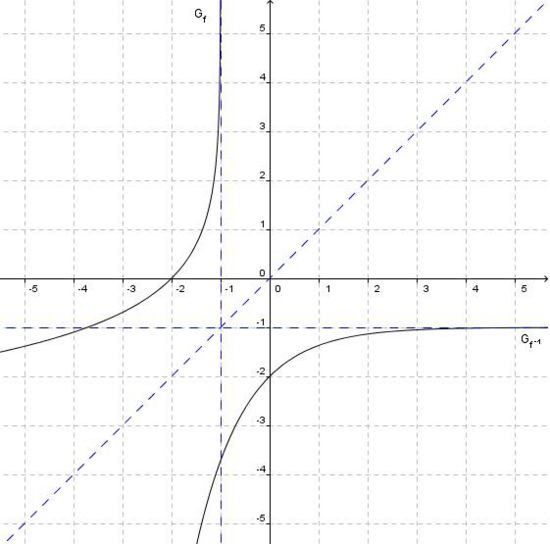
d) Skizzieren Sie unter Berücksichtigung der bisherigen Ergebnisse die Graphen der Funktionen f und <math>f^ {-1}</math> in ein Koordinatensystem. Tragen Sie dazu auch alle Asymptoten sowie die Schnittpunkte mit den Koordinatenachsen ein.<div align="right">''5 BE''</div> | d) Skizzieren Sie unter Berücksichtigung der bisherigen Ergebnisse die Graphen der Funktionen f und <math>f^ {-1}</math> in ein Koordinatensystem. Tragen Sie dazu auch alle Asymptoten sowie die Schnittpunkte mit den Koordinatenachsen ein.<div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_1d_Lös.jpg|550px]]}} |
| − | |||
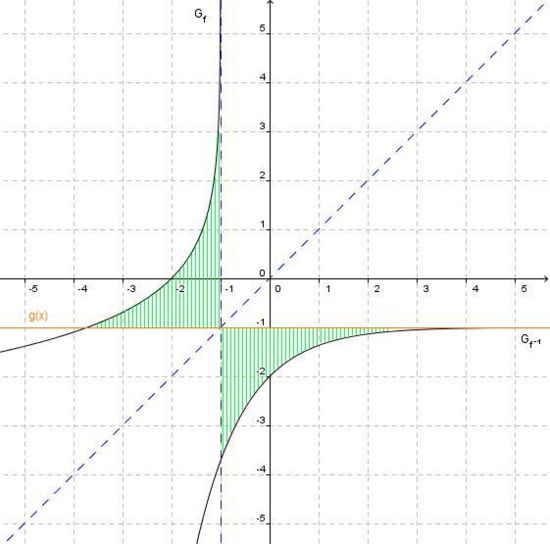
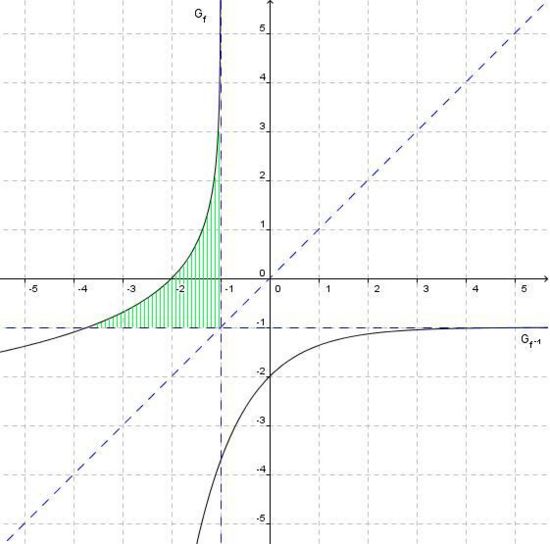
| − | + | e) Der Graph G<sub>f</sub> die x-Achse und die Gerade x= –1 schließen im zweiten Quadranten ein sich ins Unendliche erstreckendes Flächenstück mit endlichem Inhalt ein. Berechnen Sie den Inhalt dieses Flächenstücks.<div align="right">''4 BE''</div> | |
| + | 1. Lösung (einfacher) | ||
| + | <popup name="Tipp"> | ||
| + | mit Hilfe der Umkehrfunktion | ||
| + | </popup> | ||
| − | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_1e_Lös.jpg|550px]] | |
| − | :{{Lösung versteckt|1= | + | [[Bild:ABI_2005_II_1e_Lös veranschaulicht.jpg|550px]]}} |
| − | + | 2. Lösung (zeitaufwändiger und komplizierter) | |
| − | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_1e_Lös2.jpg|550px]] | |
| − | }} | + | [[Bild:ABI_2005_II_1e_Lös2 veranschaulicht.jpg|550px]]}} |
| Zeile 92: | Zeile 78: | ||
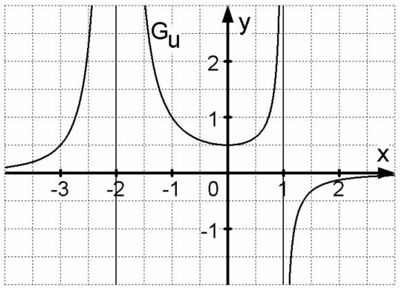
Es sei g eine in IR differenzierbare Funktion mit dem Graphen G<sub>g</sub>. Die Abbildung zeigt den Graphen G<sub>u</sub> der in IR\{-2;1} definierten Funktion <math>u:x \rightarrow u(x)={1 \over g(x)}</math>. Die x-Achse und die Geraden x= –2 und x=1 sind Asymptoten von G<sub>u</sub>. | Es sei g eine in IR differenzierbare Funktion mit dem Graphen G<sub>g</sub>. Die Abbildung zeigt den Graphen G<sub>u</sub> der in IR\{-2;1} definierten Funktion <math>u:x \rightarrow u(x)={1 \over g(x)}</math>. Die x-Achse und die Geraden x= –2 und x=1 sind Asymptoten von G<sub>u</sub>. | ||
| − | [[Bild:ABI_2005_II_Grafik_A2.jpg|center]] | + | [[Bild:ABI_2005_II_Grafik_A2.jpg|400px|center]] |
| Zeile 100: | Zeile 86: | ||
a) Geben Sie die Nullstellen von g an. Ermitteln Sie die Koordinaten der Schnittpunkte von G<sub>u</sub> und G<sub>g</sub>.<div align="right">''5 BE''</div> | a) Geben Sie die Nullstellen von g an. Ermitteln Sie die Koordinaten der Schnittpunkte von G<sub>u</sub> und G<sub>g</sub>.<div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_2a_Lös.jpg|500px]]}} |
| − | + | ||
| − | [[Bild:ABI_2005_II_2a_Lös.jpg|500px]] | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
b) Begründen Sie, dass G<sub>g</sub> in x= – 2 und x=0 waagrechte Tangenten hat.<div align="right">''5 BE''</div> | b) Begründen Sie, dass G<sub>g</sub> in x= – 2 und x=0 waagrechte Tangenten hat.<div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_2b_Lös.jpg|500px]]}} |
| − | + | ||
| − | [[Bild:ABI_2005_II_2b_Lös.jpg|500px]] | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
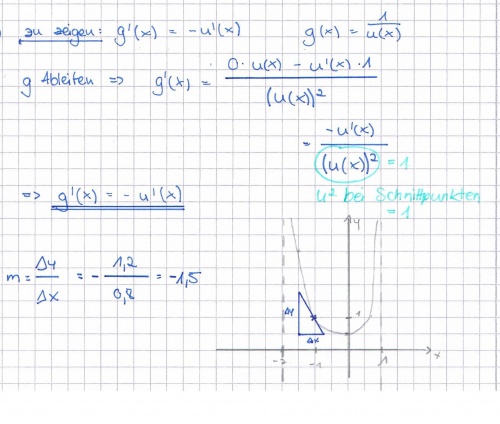
c) Zeigen Sie, dass für alle Schnittpunkte von G<sub>u</sub> und G<sub>g</sub> gilt: g' (x)= -u' (x). Ermitteln Sie g' (-1), indem Sie u' (-1) möglichst genau aus obiger Abbildung ablesen. (Entsprechende Hilfslinien sind einzuzeichnen.)<div align="right">''5 BE''</div> | c) Zeigen Sie, dass für alle Schnittpunkte von G<sub>u</sub> und G<sub>g</sub> gilt: g' (x)= -u' (x). Ermitteln Sie g' (-1), indem Sie u' (-1) möglichst genau aus obiger Abbildung ablesen. (Entsprechende Hilfslinien sind einzuzeichnen.)<div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_2c_Lös.jpg|500px]]}} |
| − | + | ||
| − | [[Bild: | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
d) Geben Sie g(0) an. Skizzieren Sie in obige Abbildung unter Berück-sichtigung der gewonnenen Ergebnisse einen möglichen Graphen G<sub>g</sub>.<div align="right">''3 BE''</div> | d) Geben Sie g(0) an. Skizzieren Sie in obige Abbildung unter Berück-sichtigung der gewonnenen Ergebnisse einen möglichen Graphen G<sub>g</sub>.<div align="right">''3 BE''</div> | ||
| − | :{{Lösung versteckt|1= | + | :{{Lösung versteckt|1=[[Bild:ABI_2005_II_2d_Lös.jpg|500px]]}} |
| − | + | ||
| − | [[Bild: | + | |
| − | + | ||
| − | + | ||
| − | }} | + | |
| − | + | ||
| − | + | ||
| − | + | ||
Aktuelle Version vom 30. März 2010, 10:57 Uhr
|
|
Gegeben ist die Funktion
4 BE
4 BE
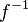 an und ermitteln Sie den Funktionsterm an und ermitteln Sie den Funktionsterm 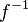 (x). (x).5 BE
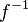 in ein Koordinatensystem. Tragen Sie dazu auch alle Asymptoten sowie die Schnittpunkte mit den Koordinatenachsen ein. in ein Koordinatensystem. Tragen Sie dazu auch alle Asymptoten sowie die Schnittpunkte mit den Koordinatenachsen ein.5 BE
4 BE
1. Lösung (einfacher) 2. Lösung (zeitaufwändiger und komplizierter)
|
Es sei g eine in IR differenzierbare Funktion mit dem Graphen Gg. Die Abbildung zeigt den Graphen Gu der in IR\{-2;1} definierten Funktion
5 BE
5 BE
5 BE
3 BE
|
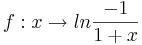 mit dem maximal möglichen Definitionsbereich D. Der Graph von f wird mit Gf bezeichnet.
mit dem maximal möglichen Definitionsbereich D. Der Graph von f wird mit Gf bezeichnet.




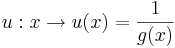 . Die x-Achse und die Geraden x= –2 und x=1 sind Asymptoten von Gu.
. Die x-Achse und die Geraden x= –2 und x=1 sind Asymptoten von Gu.