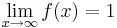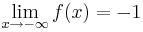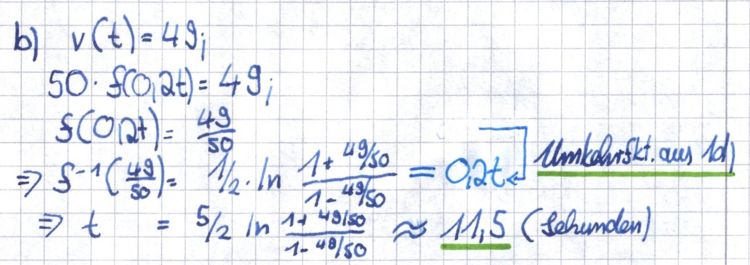2007 I: Unterschied zwischen den Versionen

Aktuelle Version vom 24. Februar 2010, 08:12 Uhr

Leistungskurs Mathematik (Bayern): Abiturprüfung 2007 Infinitesimalrechnung I

Lösungen erstellt von: Jan Kapar, Mark-André Baumer

Definitionsmenge der Umkehrfunktion: D_f^-1 = W_f = ]-1;1[, da

@@ Zeile 7: / Zeile 7: @@
 <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2007'''</big></center>
-<center><big>'''Infinitesimalrechnung II'''</big></center>
+<center><big>'''Infinitesimalrechnung I'''</big></center>
@@ Zeile 24: / Zeile 24: @@
 <tr><td  width="800px" valign="top">
-[[Bild:A1a.jpg|750px]]
+[[Bild:A1a1.jpg|750px]]
 :{{Lösung versteckt|
-[[Bild:1a.jpg|750px]]
+[[Bild:1aa.jpg|750px]]
 }}
@@ Zeile 40: / Zeile 40: @@
 :{{Lösung versteckt|
-[[Bild:1c.jpg|750px]]
+[[Bild:1cc.jpg|750px]]
 }}
 [[Bild:A1d.jpg|750px]]
-:{{Lösung versteckt|
+:{{Lösung versteckt|1=
-[[Bild:1d.jpg|750px]]
+'''Definitionsmenge der Umkehrfunktion:''' D<sub>f<sup>-1</sup></sub> = W<sub>f</sub> = ]-1;1[, da <br />
+* <math> \lim_{x\to\infty} f(x)=1 </math>
+* <math> \lim_{x\to -\infty} f(x)=-1 </math>
+* f(x) stetig ist (da aus stetigen Funktionen zusammengesetzt)
+[[Bild:1da.jpg|750px]]
 }}
 </td></tr></table></center>
@@ Zeile 63: / Zeile 68: @@
 :{{Lösung versteckt|
-[[Bild:2a.jpg|750px]]
+[[Bild:2aa.jpg|750px]]
 }}