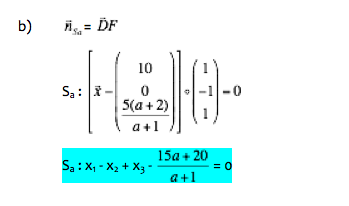2006 VI: Unterschied zwischen den Versionen
(musterseite eingefügt) |
K (Bemerkung zu Aufgabe 2a) |
||
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2006'''</big></center> | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2006'''</big></center> | ||
| − | <center><big>''' | + | <center><big>'''Analytische Geometrie VI'''</big></center> |
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media:LKM Abi 2006 | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media:LKM Abi 2006 VI lös.doc|Lösung gesamt]]</center> |
| − | <center>Erarbeitet von </center> | + | <center>Erarbeitet von Lisa Köhler, Sebastian Schirmer</center> |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 25: | Zeile 25: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | |||
| + | Gegeben ist eine Kugel K mit dem Radius 5, die in eine im Koordinatensystem stehende würfelförmige Schachtel ABCDEFGH mit der Kantenlänge 10 (siehe Abbildung) verpackt ist, sowie die Punkteschar | ||
| + | Pa(10|0|<math>\textstyle\frac{5(a+2)}{a+1}</math> ) mit dem Parameter a ∈ IR<sub>0</sub><sup>+</sup>. <br /><br /> | ||
| + | |||
| + | [[Bild:Abbildung.png]]<br /><br /> | ||
| + | |||
| + | <br /> | ||
| + | a) Wie viel Prozent des Schachtelvolumens füllt die Kugel aus? (2 BE)<br /><br /> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,1a.png|600px]] | ||
| + | }}<br /> | ||
| + | b) Berechnen Sie die Koordinaten der Punkte Z1 und Z2 , in denen die Gerade DF die Kugel schneidet. (5 BE)<br /> | ||
| + | [Zur Kontrolle: Z1(5+<math>\textstyle\frac{5}{3} </math><math>\sqrt{3}</math> |5-<math>\textstyle\frac{5}{3} </math><math>\sqrt{3}</math>|5+<math>\textstyle\frac{5}{3} </math><math>\sqrt{3}</math>)]<br /><br /> | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,1b.png|600px]]<br /> | ||
| + | [[Bild:Abi2006,1b.png|600px]] | ||
| + | }}<br /> | ||
| + | |||
| + | c) Geben Sie die kürzeste Strecke an, auf der sich der Punkt Pa bewegt, | ||
| + | wenn a das Intervall [0;∞[ durchläuft. Begründen Sie Ihre Antwort. (5 BE) | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,1c.png|600px]] | ||
}} | }} | ||
| Zeile 45: | Zeile 70: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Um diese Verpackung attraktiver zu gestalten, werden durch Ebenen, die senkrecht zu den Raumdiagonalen des Würfels verlaufen, an allen seinen Ecken kongruente dreiseitige Pyramiden abgeschnitten.<br /><br /> | ||
| + | a) Um welche besonderen Dreiecke handelt es sich bei der Grundfläche (Schnittfläche) und den Seitenflächen der abgeschnittenen Pyramiden? (3 BE)<br /><br /> | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,2a.png|600px]] | ||
| + | '''Bemerkung'''<br> | ||
| + | Die Seitenflächen sind rechtwinklig und gleichschenklig und nicht rechtwinklig und gleichseitig. | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | b) Bestimmen Sie eine Gleichung derjenigen Ebene Sa in Normalenform, die senkrecht zu DF liegt und den Punkt Pa enthält. (5 BE)<br /> | ||
| + | [mögliches Ergebnis: Sa : x1 − x2 + x3 − <math>\textstyle\frac{15a+20}{a+1}</math> = 0] | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,2b.png|600px]] | ||
| + | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
| + | |||
| + | Im Folgenden sei a = 4.<br /><br /> | ||
| + | |||
| + | a) Zeigen Sie durch Rechnung, dass die Ebene S4 die Kugel nicht | ||
| + | schneidet. (5 BE)<br /><br /> | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,3a.png|600px]] | ||
| + | }} | ||
| + | |||
| + | |||
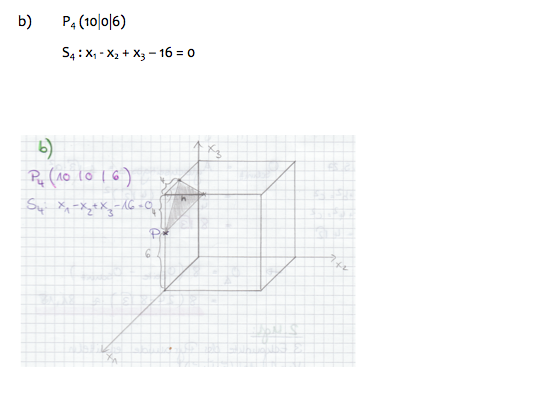
| + | b) Zeichnen Sie den Würfel, den Punkt P4 und die Schnittfläche der Ebene S4 mit dem Würfel in ein Koordinatensystem (Orientierung wie in obiger Abbildung) ein. (5 BE)<br /><br /> | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,3b.png|600px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | c) Berechnen Sie die Volumenverkleinerung der Schachtel und die Ober- flächenabnahme der Schachtel, wenn in gleicher Weise wie durch S4 | ||
| + | an der Ecke F an allen Würfelecken Pyramiden abgeschnitten werden. (6 BE)<br /><br /> | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,3c.png|600px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | d) Die Ebene S4 und die drei entsprechenden Ebenen, die die oberen | ||
| + | Ecken E, G und H des Würfels abschneiden, haben genau einen Punkt W gemeinsam (Nachweis nicht erforderlich). Berechnen Sie die Koordinaten von W. (5 BE) | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,3d.png|600px]] | ||
| + | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 16. Mai 2010, 17:25 Uhr
|
|
Gegeben ist eine Kugel K mit dem Radius 5, die in eine im Koordinatensystem stehende würfelförmige Schachtel ABCDEFGH mit der Kantenlänge 10 (siehe Abbildung) verpackt ist, sowie die Punkteschar
Pa(10|0|
b) Berechnen Sie die Koordinaten der Punkte Z1 und Z2 , in denen die Gerade DF die Kugel schneidet. (5 BE)
c) Geben Sie die kürzeste Strecke an, auf der sich der Punkt Pa bewegt, wenn a das Intervall [0;∞[ durchläuft. Begründen Sie Ihre Antwort. (5 BE)
|
Um diese Verpackung attraktiver zu gestalten, werden durch Ebenen, die senkrecht zu den Raumdiagonalen des Würfels verlaufen, an allen seinen Ecken kongruente dreiseitige Pyramiden abgeschnitten. a) Um welche besonderen Dreiecke handelt es sich bei der Grundfläche (Schnittfläche) und den Seitenflächen der abgeschnittenen Pyramiden? (3 BE)
Bemerkung
|
Im Folgenden sei a = 4. a) Zeigen Sie durch Rechnung, dass die Ebene S4 die Kugel nicht
schneidet. (5 BE)
|
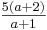 ) mit dem Parameter a ∈ IR0+.
) mit dem Parameter a ∈ IR0+. 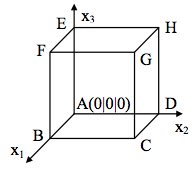

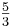
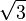 |5-
|5-


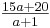 = 0]
= 0]