2009 III: Unterschied zwischen den Versionen
(Aufgabe eingefügt) |
|||
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | __NOTOC__ | |
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2009'''</big></center> | ||
| + | <center><big>'''Wahrscheinlichkeitsrechnung/Statistik III'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=79e69371e73c4c671417483e9427e728 '''Download der Originalaufgaben: Abitur 2009 LK Mathematik Bayern'''] - [[Media:LKM Abi 2009 III lös.doc|Lösungen zum Ausdrucken]]<br />Lösungen von Daniel Greb</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
Eine kleine Pension mit 5 Gästezimmern im ersten Stock und 4 weiteren im zweiten Stock wird renoviert. Die individuell gestalteten Zimmer unterscheiden sich durch Lage, Größe und Ausstattung. | Eine kleine Pension mit 5 Gästezimmern im ersten Stock und 4 weiteren im zweiten Stock wird renoviert. Die individuell gestalteten Zimmer unterscheiden sich durch Lage, Größe und Ausstattung. | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| − | + | ;Aufgabe 1 | |
Für die Bäderrenovierung der Gästezimmer bestellt der Pensionsinhaber 2500 Fliesen. Aus Kostengründen entscheidet er sich für Fliesen II. Wahl, wobei der Verkäufer versichert, dass höchstens 10 % derartiger Fliesen fehlerhaft sind. Die Fliesen werden in Kartons zu je 50 Stück geliefert. | Für die Bäderrenovierung der Gästezimmer bestellt der Pensionsinhaber 2500 Fliesen. Aus Kostengründen entscheidet er sich für Fliesen II. Wahl, wobei der Verkäufer versichert, dass höchstens 10 % derartiger Fliesen fehlerhaft sind. Die Fliesen werden in Kartons zu je 50 Stück geliefert. | ||
| Zeile 43: | Zeile 68: | ||
}} | }} | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| − | == | + | |
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
Nach der Renovierung kommen die ersten 5 Übernachtungsgäste gleichzeitig an: 3 Frauen und 2 Männer. Jeder Gast möchte ein eigenes Zimmer. | Nach der Renovierung kommen die ersten 5 Übernachtungsgäste gleichzeitig an: 3 Frauen und 2 Männer. Jeder Gast möchte ein eigenes Zimmer. | ||
| Zeile 60: | Zeile 92: | ||
}} | }} | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| − | == | + | |
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
Eine Zufallsgröße X mit der Wertemenge {0;1;2;3} und Erwartungswert 1 hat folgende Verteilung: | Eine Zufallsgröße X mit der Wertemenge {0;1;2;3} und Erwartungswert 1 hat folgende Verteilung: | ||
| Zeile 76: | Zeile 115: | ||
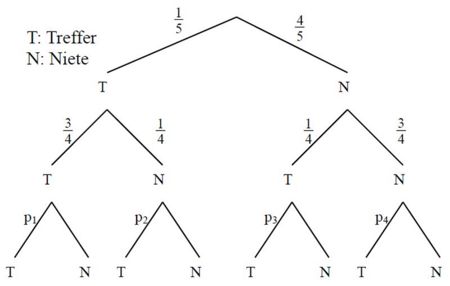
c) Die Zufallsgröße X gibt die Anzahl der Treffer bei einem dreistufigen Zufallsexperiment an. Dieses Zufallsexperiment wird durch das unten stehende Baumdiagramm beschrieben. Berechnen Sie p<sub>1</sub> und p<sub>4</sub> und ermitteln Sie je einen möglichen Wert für p<sub>2</sub> und p<sub>3</sub> so, dass sich mit diesen vier Werten die Verteilung der Zufallsgröße X ergibt. | c) Die Zufallsgröße X gibt die Anzahl der Treffer bei einem dreistufigen Zufallsexperiment an. Dieses Zufallsexperiment wird durch das unten stehende Baumdiagramm beschrieben. Berechnen Sie p<sub>1</sub> und p<sub>4</sub> und ermitteln Sie je einen möglichen Wert für p<sub>2</sub> und p<sub>3</sub> so, dass sich mit diesen vier Werten die Verteilung der Zufallsgröße X ergibt. | ||
| + | |||
| + | [[Bild:ABI 2009 III Grafik A3.jpg|450px|center]] | ||
| + | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
[[Bild:ABI_2009_III_3_Lös.jpg|750px]] | [[Bild:ABI_2009_III_3_Lös.jpg|750px]] | ||
}} | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 10. Februar 2010, 10:56 Uhr
|
Lösungen von Daniel Greb |
|
Eine kleine Pension mit 5 Gästezimmern im ersten Stock und 4 weiteren im zweiten Stock wird renoviert. Die individuell gestalteten Zimmer unterscheiden sich durch Lage, Größe und Ausstattung. |
Für die Bäderrenovierung der Gästezimmer bestellt der Pensionsinhaber 2500 Fliesen. Aus Kostengründen entscheidet er sich für Fliesen II. Wahl, wobei der Verkäufer versichert, dass höchstens 10 % derartiger Fliesen fehlerhaft sind. Die Fliesen werden in Kartons zu je 50 Stück geliefert.
|
Nach der Renovierung kommen die ersten 5 Übernachtungsgäste gleichzeitig an: 3 Frauen und 2 Männer. Jeder Gast möchte ein eigenes Zimmer.
|
Eine Zufallsgröße X mit der Wertemenge {0;1;2;3} und Erwartungswert 1 hat folgende Verteilung:
|


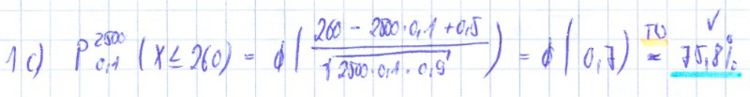


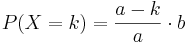 mit k ∈ {0; 1; 2; 3} und a,b ∈ IR+ .
mit k ∈ {0; 1; 2; 3} und a,b ∈ IR+ .