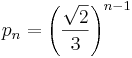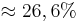2009 IV: Unterschied zwischen den Versionen
K (Bemerkung zu Aufgabe 3c) |
|||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | |
| − | + | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2009'''</big></center> | ||
| + | <center><big>'''Wahrscheinlichkeitsrechnung/Statistik IV'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=79e69371e73c4c671417483e9427e728 '''Download der Originalaufgaben: Abitur 2009 LK Mathematik Bayern'''] - [[Media:LKM Abi 2009 IV lös.doc|Lösungen zum Ausdrucken]]</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
Die folgenden Angaben zum Rauchverhalten beziehen sich auf den Drogen- und Suchtbericht der Bundesregierung aus dem Jahr 2008. Personen, die regelmäßig rauchen, werden unabhängig vom Geschlecht als Raucher bezeichnet. Die anderen Personen werden als Nichtraucher bezeichnet. | Die folgenden Angaben zum Rauchverhalten beziehen sich auf den Drogen- und Suchtbericht der Bundesregierung aus dem Jahr 2008. Personen, die regelmäßig rauchen, werden unabhängig vom Geschlecht als Raucher bezeichnet. Die anderen Personen werden als Nichtraucher bezeichnet. | ||
| Zeile 8: | Zeile 27: | ||
Ein Drittel der Erwachsenen in Deutschland sind Raucher. | Ein Drittel der Erwachsenen in Deutschland sind Raucher. | ||
| + | |||
a) Mit welcher Wahrscheinlichkeit sind unter 15 zufällig ausgewählten Erwachsenen mehr als die Hälfte Nichtraucher? | a) Mit welcher Wahrscheinlichkeit sind unter 15 zufällig ausgewählten Erwachsenen mehr als die Hälfte Nichtraucher? | ||
| − | b) Es werden zufällig nacheinander n Erwachsene befragt. Die Wahrscheinlichkeit dafür, dass bei der Befragung Raucher und Nichtraucher einander immer abwechseln, werde mit bezeichnet, wobei der erste Befragte Raucher oder Nichtraucher sein kann. Zeigen Sie, dass für eine ungerade Anzahl gilt: | + | |
| + | b) Es werden zufällig nacheinander n Erwachsene befragt. Die Wahrscheinlichkeit dafür, dass bei der Befragung Raucher und Nichtraucher einander immer abwechseln, werde mit bezeichnet, wobei der erste Befragte Raucher oder Nichtraucher sein kann. Zeigen Sie, dass für eine ungerade Anzahl n <math>\ge </math> 3 gilt: | ||
| + | |||
| + | :<math>p_n = \left( \frac {\sqrt{2}}{3} \right)^{n-1}</math> | ||
| + | |||
| + | |||
c) Ab welcher Anzahl n ist die Wahrscheinlichkeit aus Teilaufgabe 1b kleiner als ein Milliardstel? | c) Ab welcher Anzahl n ist die Wahrscheinlichkeit aus Teilaufgabe 1b kleiner als ein Milliardstel? | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI_2009_4_A1_Lös.jpg|800px]] | ||
| + | }} | ||
| − | == | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
Im Jahr 2005 waren 20% der 12- bis 17-jährigen Jugendlichen Raucher. Es wird vermutet, dass durch diverse Kampagnen diese Raucherquote auf 18% gesenkt werden konnte. Um diese Vermutung zu testen, werden 500 Jugendliche dieser Altersgruppe anonym befragt. Die Nullhypothese ''Mindestens 20% der Jugendlichen sind Raucher'' wird abgelehnt, wenn weniger als 19% der Befragten regelmäßig rauchen. Berechnen Sie unter der Annahme, dass die Kampagnen so erfolgreich waren wie vermutet, die Wahrscheinlichkeit für den Fehler 2. Art. Verwenden Sie die Normalverteilung als Näherung. | Im Jahr 2005 waren 20% der 12- bis 17-jährigen Jugendlichen Raucher. Es wird vermutet, dass durch diverse Kampagnen diese Raucherquote auf 18% gesenkt werden konnte. Um diese Vermutung zu testen, werden 500 Jugendliche dieser Altersgruppe anonym befragt. Die Nullhypothese ''Mindestens 20% der Jugendlichen sind Raucher'' wird abgelehnt, wenn weniger als 19% der Befragten regelmäßig rauchen. Berechnen Sie unter der Annahme, dass die Kampagnen so erfolgreich waren wie vermutet, die Wahrscheinlichkeit für den Fehler 2. Art. Verwenden Sie die Normalverteilung als Näherung. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI_2009_4_A2_Lös.jpg|800px]] | ||
| + | }} | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
| − | |||
Im Folgenden werden ausschließlich Schülerinnen und Schüler der Sekundarstufe I, die die Jahrgangsstufen 5-10 umfasst, betrachtet. Von diesen besuchen in Bayern jeweils 35 % eine Hauptschule beziehungsweise ein Gymnasium. Vereinfachend werde angenommen, dass die Übrigen eine Realschule besuchen. | Im Folgenden werden ausschließlich Schülerinnen und Schüler der Sekundarstufe I, die die Jahrgangsstufen 5-10 umfasst, betrachtet. Von diesen besuchen in Bayern jeweils 35 % eine Hauptschule beziehungsweise ein Gymnasium. Vereinfachend werde angenommen, dass die Übrigen eine Realschule besuchen. | ||
Es soll angenommen werden, dass die folgenden Raucherquoten aus dem Bericht der Bundesregierung auch für Bayern gelten: In der Sekundarstufe I sind insgesamt 16% Raucher; an Hauptschulen ist die Quote der Raucher mit 24% mehr als dreimal so hoch wie an Gymnasien mit 7%. | Es soll angenommen werden, dass die folgenden Raucherquoten aus dem Bericht der Bundesregierung auch für Bayern gelten: In der Sekundarstufe I sind insgesamt 16% Raucher; an Hauptschulen ist die Quote der Raucher mit 24% mehr als dreimal so hoch wie an Gymnasien mit 7%. | ||
| Zeile 28: | Zeile 77: | ||
a) Wie groß ist die Raucherquote an Realschulen? Mit welcher Wahrscheinlichkeit besucht ein aus der Sekundarstufe I zufällig ausgewählter Raucher ein Gymnasium? [Teilergebnis: Raucherquote an Realschulen: 17%] | a) Wie groß ist die Raucherquote an Realschulen? Mit welcher Wahrscheinlichkeit besucht ein aus der Sekundarstufe I zufällig ausgewählter Raucher ein Gymnasium? [Teilergebnis: Raucherquote an Realschulen: 17%] | ||
| + | |||
b) Mit welcher Wahrscheinlichkeit besuchen 2 aus der Sekundarstufe I zufällig ausgewählte Personen die gleiche Schulart und mindestens eine der beiden Personen raucht regelmäßig? | b) Mit welcher Wahrscheinlichkeit besuchen 2 aus der Sekundarstufe I zufällig ausgewählte Personen die gleiche Schulart und mindestens eine der beiden Personen raucht regelmäßig? | ||
| + | |||
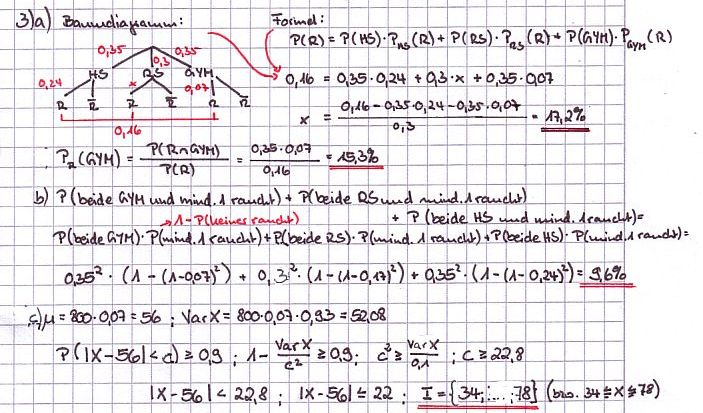
c) An einem Gymnasium besuchen 800 Schüler die Klassen 5 bis 10, von denen jeder mit einer Wahrscheinlichkeit von 7 % regelmäßig raucht. Geben Sie mit Hilfe der Ungleichung von Tschebyschow ein möglichst kleines Intervall symmetrisch um den Erwartungswert an, in dem die Zahl der regelmäßigen Raucher der Sekundarstufe I mit einer Wahrscheinlichkeit von mindestens 90% liegt. | c) An einem Gymnasium besuchen 800 Schüler die Klassen 5 bis 10, von denen jeder mit einer Wahrscheinlichkeit von 7 % regelmäßig raucht. Geben Sie mit Hilfe der Ungleichung von Tschebyschow ein möglichst kleines Intervall symmetrisch um den Erwartungswert an, in dem die Zahl der regelmäßigen Raucher der Sekundarstufe I mit einer Wahrscheinlichkeit von mindestens 90% liegt. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI_2009_4_A3_Lös.jpg|800px]] | ||
| + | }} | ||
| + | |||
| + | <popup name="Bemerkung"> | ||
| + | '''zu c)''' Da c<math>\ge</math>22,82 und damit c<math>\ge</math>23 ist das Intervall I={33;...;79}. | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 4 | ||
| − | |||
a) An einem Gymnasium werden die 38 Interessenten am Grundkurs Physik, von denen 12 regelmäßig rauchen, auf 2 Kurse mit 18 beziehungsweise 20 Teilnehmern zufällig verteilt. Mit welcher Wahrscheinlichkeit sind in jedem der beiden Kurse gleich viele Raucher? | a) An einem Gymnasium werden die 38 Interessenten am Grundkurs Physik, von denen 12 regelmäßig rauchen, auf 2 Kurse mit 18 beziehungsweise 20 Teilnehmern zufällig verteilt. Mit welcher Wahrscheinlichkeit sind in jedem der beiden Kurse gleich viele Raucher? | ||
| + | |||
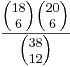
b) Für die K12 eines Gymnasiums sind im Fach Geschichte 4 Kurse mit jeweils mindestens 20 Teilnehmern eingerichtet worden. Wie viele verschiedene Aufteilungen der 20 Raucher der K12 auf diese 4 Kurse sind prinzipiell möglich, wenn nur zwischen Rauchern und Nichtrauchern unterschieden wird? | b) Für die K12 eines Gymnasiums sind im Fach Geschichte 4 Kurse mit jeweils mindestens 20 Teilnehmern eingerichtet worden. Wie viele verschiedene Aufteilungen der 20 Raucher der K12 auf diese 4 Kurse sind prinzipiell möglich, wenn nur zwischen Rauchern und Nichtrauchern unterschieden wird? | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI_2009_4_A4_Lös.jpg|800px]]<br /> | ||
| + | '''Alternativlösung''' zur Teilaufgabe a):<br /> | ||
| + | Man betrachtet beide Kurse, wobei in jedem 6 Raucher sein sollen (ebenfalls Urnenmodell ohne Zurücklegen):<br /> | ||
| + | P(X=6) = <math>\frac{{18 \choose 6}{20 \choose 6}}{{38 \choose 12}}</math> <math>\approx 26,6%</math> | ||
| + | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 6. April 2010, 10:52 Uhr
|
|
Die folgenden Angaben zum Rauchverhalten beziehen sich auf den Drogen- und Suchtbericht der Bundesregierung aus dem Jahr 2008. Personen, die regelmäßig rauchen, werden unabhängig vom Geschlecht als Raucher bezeichnet. Die anderen Personen werden als Nichtraucher bezeichnet. Ein Drittel der Erwachsenen in Deutschland sind Raucher.
c) Ab welcher Anzahl n ist die Wahrscheinlichkeit aus Teilaufgabe 1b kleiner als ein Milliardstel? |
Im Jahr 2005 waren 20% der 12- bis 17-jährigen Jugendlichen Raucher. Es wird vermutet, dass durch diverse Kampagnen diese Raucherquote auf 18% gesenkt werden konnte. Um diese Vermutung zu testen, werden 500 Jugendliche dieser Altersgruppe anonym befragt. Die Nullhypothese Mindestens 20% der Jugendlichen sind Raucher wird abgelehnt, wenn weniger als 19% der Befragten regelmäßig rauchen. Berechnen Sie unter der Annahme, dass die Kampagnen so erfolgreich waren wie vermutet, die Wahrscheinlichkeit für den Fehler 2. Art. Verwenden Sie die Normalverteilung als Näherung. |
Im Folgenden werden ausschließlich Schülerinnen und Schüler der Sekundarstufe I, die die Jahrgangsstufen 5-10 umfasst, betrachtet. Von diesen besuchen in Bayern jeweils 35 % eine Hauptschule beziehungsweise ein Gymnasium. Vereinfachend werde angenommen, dass die Übrigen eine Realschule besuchen. Es soll angenommen werden, dass die folgenden Raucherquoten aus dem Bericht der Bundesregierung auch für Bayern gelten: In der Sekundarstufe I sind insgesamt 16% Raucher; an Hauptschulen ist die Quote der Raucher mit 24% mehr als dreimal so hoch wie an Gymnasien mit 7%.
|
a) An einem Gymnasium werden die 38 Interessenten am Grundkurs Physik, von denen 12 regelmäßig rauchen, auf 2 Kurse mit 18 beziehungsweise 20 Teilnehmern zufällig verteilt. Mit welcher Wahrscheinlichkeit sind in jedem der beiden Kurse gleich viele Raucher?
|
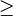 3 gilt:
3 gilt: