Versuchsprotokolle: Unterschied zwischen den Versionen
(→Franziska, Pia, Stefanie, Tonja: Daten in Tabelle formatiert, Inhalt übersichtlich gestaltet) |
(Ausdruck verbessert) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 160: | Zeile 160: | ||
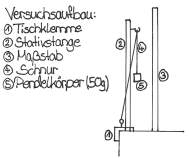
'''Versuchsablauf:'''<br> | '''Versuchsablauf:'''<br> | ||
| − | Der Pendelkörper | + | Der Pendelkörper wird mit einer beliebigen Schnur- bzw. Pendellänge, die mit Hilfe des Maßstabs (oder Lineal) bestimmt wird, in einem beliebigen Winkel (im Verhältnis zur Stativstange) ausgelenkt und dann losgelassen. |
| + | Die Zeit, die der Körper für zehn komplette Schwingungen benötigt, wird mit Hilfe einer Stoppuhr gemessen. | ||
| + | Für jede Pendellänge werden zwei Messungen durchgeführt. Aus den sich ergebenden Werten wird ein Mittelwert für die Zeit errechnet. | ||
| + | Die darauffolgenden Messdurchgänge werden auf die gleiche Weise durchgeführt, allerdings jedes Mal mit einer anderen Pendellänge. | ||
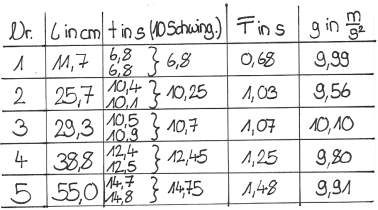
'''Messwerte:'''<br> | '''Messwerte:'''<br> | ||
[[Bild:MesswertezuPendelversuchPR.jpg]] | [[Bild:MesswertezuPendelversuchPR.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | '''Auswertung'''<br> | ||
| + | Der errechnete Mittelwert für die Zeit wird nun durch die Anzahl der Schwingungen geteilt, um die Schwingungsdauer T zu erhalten. Man misst dafür nicht nur direkt die Zeit für eine Schwingung, sonderm z.B. für zehn, da das Ergebnis so genauer ist. | ||
| + | Mit Hilfe der Formel <math>T=2\pi\sqrt{\frac{l}{g}}</math><br>kann nun durch Umstellen der Ortsfaktor g errechnet werden. | ||
| + | Die Formel lautet dann: <math>g=\frac{l(2\pi)^2}{T^2}</math> | ||
| Zeile 187: | Zeile 197: | ||
| − | '''Messabweichungen | + | '''Ursachen für Messabweichungen:''' |
| − | <br> - | + | <br> - Auslenkungswinkel nicht genau gleich bei den verschiedenen Messungen |
| − | <br> - | + | <br> - Länge des Fadenpendels nicht exakt abgelesen |
| + | <br> - ungenaue Zeitmessung durch Reaktionszeit | ||
| + | <br> - Reibung wurde nicht berücksichtigt | ||
Aktuelle Version vom 27. Januar 2010, 22:00 Uhr
Schülerversuch: Zusammenhang zwischen der Pendellänge und der Periodendauer beim Fadenpendel
Hinweis: Gruppe 1 ist die Gruppe, die sich zuerst einträgt usw.
Inhaltsverzeichnis |
Tina, Elena, Sebastian, Thomas
Materialen, die man für diesen Versuch benötigt:
- Gestell
- Gewichtsstück (50g)
- Metermaß
- Schnur
- Haken zum Befestigen des Gewichtstückes
- Stoppuhr
Versuchsaufbau
Der Faden, an dem das Gewichtstück befestigt worden ist, wird an dem Haken am Gestell befestigt.
Durchführung
Der Versuch wird jeweils bei unterschiedlicher Schnurlänge durchgeführt. Zuerst wird das Gewichtstück um einen bestimmtem Winkel ausgelenkt, was bei unserem Versuch 20 Grad war. Wir haben jeweils 10 Schwingungen gemessen und davon die Zeit gemessen. Diesen Vorgang haben wir dann öfter durchgeführt, um einen Durchschnittswert von den Messungen zu bekommen, um auf diese Weise genauere Werte zu erhalten.
Markus , Julian, Felix G., Felix F.
Benötigte Materialien:
- -Metermaß
- -Schnur
- -Gewichtsstück(e)
- -Stopuhr
- -Haken zum Befestigen
Durchführung:
Man hängt eine Schnur mit einem Gewichtsstück an den Haken vom Stab. Anschließend misst man 10cm Schnurlänge.
Das Fadenpendel wird um einen bestimmten Winkel (z.B. 20°) in Schwingung gesetzt.
Nun wird die Zeit von 10 Schwingungen gemessen.
Das gleiche macht man mit einer Schnurlänge von 20cm, 30cm, 40cm und 50cm.
Die Masse des Gewichts, das an der Schnur hängt, ist egal.
Messwerte:
| Pendellänge l in cm | Schwingungsdauer T in s |
| 10 | 6,3 |
| 20 | 9,0 |
| 30 | 11,0 |
| 40 | 12,6 |
| 50 | 14,2 |
Daraus ergibt sich pro Schwingung eine Zeit von:
- Für 10 cm: 0,63s
- Für 20 cm: 0,90s
- Für 30 cm: 1,10s
- Für 40 cm: 1,26s
- Für 50 cm: 1,42s
Anmerkungen:
Für 10 cm: Fallbeschleunigung g = 9,95 m/s2
Für 20 cm: Fallbeschleunigung g = 9,74 m/s2
Für 30 cm: Fallbeschleunigung g = 9,79 m/s2
Für 40 cm: Fallbeschleunigung g = 9,95 m/s2
Für 50 cm: Fallbeschleunigung g = 9,79 m/s2
Abweichungen durch folgende Gründe:
- -Luftwiderstand
- -Keine exakte Pendellänge
- -Reaktion an der Stopuhr
- -Reibung an Schwingungsursprung
Grafische Darstellung:
Albin, Patrik, Dominik, Christoph
Verwendete Materialien
- Schnur
- Gewichte
- Gestell
- Haken zum Halten des Gewichts
- Stoppuhr
Versuchsaufbau
Das Gewicht mit dem Faden und dem Haken am Gestell befestigen. Siehe Bild (kommt noch):
Durchführung
Das Gewicht mit einer bestimmten Schnurlänge um einen gewissen Winkel auslenken, die Schwinungsdauer mit der Stoppuhr messen. Damit die Messung genauer wird, misst man statt einer Schwingung zehn und teilt die Zeit dann durch zehn. In den nächsten Messdurchgängen variiert man entweder Pendelänge, Auslenkung oder beides. Man notiert jeweils die Ergebnisse.
Aus den Werten für Pendellänge l und Schwinungsdauer T kann man mit der Formel
=> 
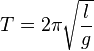
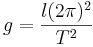den Ortsfaktor für die jeweiligen Schwinungen berechnen. Die Abweichung zum tatsächlichen Ortsfaktor (
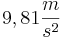) ergibt sich durch Ungenauigkeiten beim Stoppen der Zeit und beim Abmessen der Pendellänge.
Katharina, Julia, Christian, Anna, Nicole
Gemessen:
-Pendellänge nach Einstellen des Pendels
-für 25 Schwingungen benötgte Zeit gemessen
- 3 Durchgänge pro Pendellänge
| Auslenkung | Pendellänge | Durchschnittliche Schwingungsdauer | Fallbeschleunigung g (Abweichung) |
| 20° | 18,5 cm | 0,88 s | 9,43 m/s² (3,9%) |
| 20° | 26,0 cm | 1,07 s | 8,97 m/s² (8,6%) |
| 20° | 35,0 cm | 1,22 s | 9,28 m/s² (5,4%) |
| 20° | 47,0 cm | 1,36 s | 9,94 m/s² (1,3%) |
Durch die Messfehler bei der Zeitmessung ergeben sich Ungenauigkeiten, weil man nie genau am Ende der Schwingung die Zeit stoppen kann.
Max Welsch, Maximilian Werb, Christopher Scholl, Johannes Bettinger
Simon, Felix K., Barbara, Lea
Franziska, Pia, Stefanie, Tonja
Versuchsablauf:
Der Pendelkörper wird mit einer beliebigen Schnur- bzw. Pendellänge, die mit Hilfe des Maßstabs (oder Lineal) bestimmt wird, in einem beliebigen Winkel (im Verhältnis zur Stativstange) ausgelenkt und dann losgelassen.
Die Zeit, die der Körper für zehn komplette Schwingungen benötigt, wird mit Hilfe einer Stoppuhr gemessen.
Für jede Pendellänge werden zwei Messungen durchgeführt. Aus den sich ergebenden Werten wird ein Mittelwert für die Zeit errechnet.
Die darauffolgenden Messdurchgänge werden auf die gleiche Weise durchgeführt, allerdings jedes Mal mit einer anderen Pendellänge.
Messwerte:
Auswertung
Der errechnete Mittelwert für die Zeit wird nun durch die Anzahl der Schwingungen geteilt, um die Schwingungsdauer T zu erhalten. Man misst dafür nicht nur direkt die Zeit für eine Schwingung, sonderm z.B. für zehn, da das Ergebnis so genauer ist.
Mit Hilfe der Formel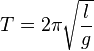
kann nun durch Umstellen der Ortsfaktor g errechnet werden.
Die Formel lautet dann: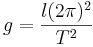
Abweichungen der erhaltenen Werte für g (in m/s²):
| errechneter Wert für g | Prozentuale Abweichung* |
| 9,99 | 1,8 % |
| 9,56 | 2,5 % |
| 10,10 | 3,0 % |
| 9,80 | 0,01 % |
| 9,91 | 0,10 % |
| → Ø Abweichung: | 0,06 % |
* Prozentuale Abweichung: Es wurde g=9,81m/s² als Normalwert angenommen.
Ursachen für Messabweichungen:
- Auslenkungswinkel nicht genau gleich bei den verschiedenen Messungen
- Länge des Fadenpendels nicht exakt abgelesen
- ungenaue Zeitmessung durch Reaktionszeit
- Reibung wurde nicht berücksichtigt
