Aktuelle Version vom 27. Januar 2010, 15:59 Uhr

Inhaltsverzeichnis

1 Verschieben von Funktionsgraphen

Verschieben von Funktionsgraphen

1.Verschiebung nach oben/unten

Problemstellung:


Im nebenstehenden Applet siehst du den Funktionsgraphen f der Funktion f(x)=x³. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt.

Erklärung:
Der Graph f gehört zu dem Funktionsterm f(x)=x³. Der rote Graph g liegt jeweils so viele Einheiten über bzw. unter dem Graphen f, wie der Regler anzeigt.
Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet bespielsweise für a=3, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings um a Einheiten nach oben (in positiver y-Richtung) bzw. nach unten (in negativer y-Richtung) verschoben.

Für den Funktionsterm g(x) gilt somit: g(x)=f(x)+a.

Beispiel: f(x)=x³

f(1)=1

Verschiebung um 3 Einheiten nach oben → g(x)=f(x)+3

g(1)=f(1)+3

g(1)=1+3

g(1)=4

Merke:

Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x)+a entsteht der Graph g durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung.

Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten).

2.Verschiebung nach rechts/links

Problemstellung:
Im untenstehenden Applet siehst du den Graphen f mit x→x³+2x² und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst.
Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauszufinden.

Erklärung:
Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben
nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings um b Einheiten nach rechts bzw. links verschoben. Somit entspricht
der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.
Das bedeutet für den funktionellen Zusammenhang: g(x)=f(x-3).

Beispiel: f(x)=x³+2x²

x=1 → f(1)=3

Verschiebung um 3 Einheiten nach rechts:

g(x)=f(x-3)

g(x)=(x-3)³+2(x-3)²

g(4)=(4-3)³+2(4-3)²

g(4)=1+2=3=f(1)

Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von g(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.

Merke:
Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).

3.Beispielaufagben

Aufgabe 1:
Gegeben ist die Funktion f(x)=x³+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.

Lösung anzeigen

Aufgabe 2:
Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x³ hervorgegangen sind.

Ausgangsfunktion:

a)

b)

c)

Lösung anzeigen

Aufgabe 3:

Kreuze an, was stimmt. Es können mehrere Antwortmöglichkeiten richtig sein.

Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen

Zurück zur Übersicht

@@ Zeile 1: / Zeile 1: @@
+{|
+! width="910" |
+|-
+| valign="top" |
 = <span style="color: blue">Verschieben von Funktionsgraphen</span> =
 ==<span style="color: blue">1.Verschiebung nach oben/unten</span> ==
-'''<span style="color: blue">Problemstellung:</span>'''
+'''<span style="color: blue">Problemstellung:</span>''' <br />
-<ggb_applet width="892" height="512"  version="3.2" ggbBase64="UEsDBBQACAAIAAORMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vffb9s2EH5e/wpCTy2GxJI8Fw1gpUg6FAiQNQPcdUAfBlDSWeJMkRpJOXL++h2PkuMfXeCs3QbsieLxdLr77uNHav62byRbg7FCqyxKzuOIgSp0KVSVRZ1bnr2J3l6+mFegK8gNZ0ttGu6yaHqeRt7eicsX381tre8Zl+TyScB9FjnTQcRsa4CXtgZwwbzk0qKdd72QgpvNXf47FM4+LoQYN6rt3BikaMpbYcfphL7XSuF+FGtRgmFSF1n0eoaZ49MnME4UXGbRD3GwpFmUHiyiaepXa23Eg1bOuz8GX6KFMSseAAFJvW0+oTrn0BVSlIIrXwzlgU6M3YvS1ZjC9DWGBFHVmOssiUO0QmtTLjbWQcP6z2A0ppPMPM6bMJuGmcW88IOzmJZ2ZxQG1gtwDrtiGe/BjthURpS7zzf2WstyC2erhXLveOs6Qw2dDqaF2/jw+CXj071SlYTBliLgNRSrXPeLAME0hP64aekVSiev3mmpDTMe3Bk6DGMeRvLxeW69YvKJyWOI4YNu15OLlDxozMNIXlKokNpQdzIWPQLMe2GZN3gQkYcjHJLngH2NWKeEux0n2P/VUGkS/D90TY7832XANmTyjULOJwfUma/AKJCBIAr72unOsrUnYmgd5VFCIRqchoUBEO6b9QsmEKwlVAbGvMPuCXDR6h4JD8zzyZiEz8FiroVDFcB6nK8FN4stagE5KLZG8/tOrfy6rQxva1B+FzvcQVn0HnuIlbFfhVxFrOQO3/biAD1uf+uVJSDHsDiUl77F8WX/imWs/+3l9Dx+RdmAhAZw5zni2bJTlM0W9GW0zwZXI+wKwxNl3S45SY00KctB5x5bjMt/wU3UoLbm+DRuPck3qDK7cFK0n3S5DzJX2CxCEDd76wN4OrQA5SCsY5KsxZC0H3d6fUJlyKKA0RFaqmvAiGJbJyewMLluSDE5/8bYJCdiM/hZSVLdCDxkzkjvGt6jvvknnlstOweLAomsbnVBII7ZDeKaxCSM+M6bC1JI1NvUPyxFD4+C92VFP4k1X9O+vc4csD6LqoH01R7p2feMR+wE5lf/HPNH7X4u9++WSwvOd+MsvaBmPLkznsntQjcNVyVTvMHln/2BRRAIfytgPPZiEErp3Gi5CkGGV49ApVNvC8ZVdATWwJ8n0UrSgBaNw0n3H6kFCbr1DUiG3UDjw85ODwe9v6DQZ6fPR7k6Qvn6OShf/w9RTr8O5QVU3n6A8xXWlwzg7sFdPg23HaKNeJb/zhH59xqSHEJ6NmIaH2J6UgXwhwo+Nly9RIP/BIVwWxClb+eNcniNARLU4/vVCqD119o79dFwZf2/TfDZubdtOznZvSTRP8HwT3T5J1BLBwgqgdzw+gMAAEUNAABQSwECFAAUAAgACAADkTI8KoHc8PoDAABFDQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAADQEAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
+{|
-Im nebenstehenden Koordinatensystem siehst du den Funktionsgraphen f der Funktion f(x)=x<sup>3</sup>. Der rote Graph h liegt 3 Einheiten über dem Graphen von f. Welcher formelle Zusammenhang besteht nun zwischen den beiden Graphen f und h? <br /> <br /> <br />
+! width="370" |
+! width="40" |
+|-
+| valign="top" |
+<br /> Im nebenstehenden Applet siehst du den Funktionsgraphen f der Funktion f(x)=x<sup>3</sup>. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben
+des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt. <br /> <br />
+|
+| valign="top" |
+<ggb_applet width="530" height="503"  version="3.2" ggbBase64="UEsDBBQACAAIAMmINzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Zdfb9s2EMCf109B6KnFEFt/4iAGrBRJhwIBsmaAuw7owwBaOsucJVIjKUfOp9/xSDm20wbJ2m3Anigdj6e73x2P1Oxt39RsA9oIJfMoGcURA1moUsgqjzq7PDmP3l68mlWgKlhozpZKN9zmUTZKIyfvxMWrH2Zmpe4Yr0nlk4C7PFry2kDETKuBl2YFYA/kvOtFLbje3i7+gMKahwlv5Fq2HX7F6g5lRVPeCDO8jumDbS3sT2IjStCsVkUenU3QdXz6BNqKgtd5dBp7SZpH6dEkijI3u1Ja3CtpnfqD8SVKGDPiHpDImZPNxhToDLqiFqXg0gVDfqASY3eitKs8mmTOJIhqhb5O4sRbK5TS5XxrLDSs/wxaOXemDvQ2vJ0TdoN+gVtHU+EtOx2dnWfx9HwyTSan03R65o3CZg7WYpIM4z2YgVSlRbn/fG2uVF3u4LZKSPuOt7bTlN8siOZ26z6G39XO+UtZ1RBkKeJfQbFeqH7ugWTe9MdtS0vInUX1TtVKM+1im6BCGBd+JB3n504rJp2YNIINZ3Q3n0xT0qBx4UfSqoX0roW4syHoJB4+IwxzAocUy3LAUfMFYJYj1klhb4YXrIZ1iDTx+h+6ZoHbYb8ediaT72RyNj4qpNkatITal4vEvHaqM2zjytKnjvwooRANvvqJAIS7ZP2KDnhpCZWGwW+/lzwumo33S/JIPBsPTjgfDPpaWGwKGI91seDWMcVKwAIk26D4fSfXbt5UmrcrkG5PW9xPefQec4iRsd9EvY5YyS2udr0CemwGxjUaT45hcNht+hbH1/0blrP+99fZKH5D3kANDeA+tFRny06SNzvoy+iwGuwKsUs0j/s+CotCtNScFPWZo8w9pBinv1Kb2JHaFcenUTBX8y32nH2cZO1nVR5C5hKTRQRx67fOgCuHFqAMfXZwkrVokvbjXq6fERlWkWf0iJbsGtCi2MXJCRY61wUX09F3ZpM8k03QMzU17kbgmXMycTAa3mPvc098YVTdWZgXWMjyRhUEcfAutNokpjbp1pxRv0Q4tHopenhoeF/u719kmx5Vzbek7yAzR1WfR1Uo+uqg6NmPjEfsGZVf/XOVP/Tul9b+7XJpwLpsnKRTSsaTO+OFtV2opuGyZJI3OP2LO7AIgXB3BMZj1wx8KJ0dJJfeSFj6CCqdejsYl9EjWKF+nqSVpJ4WjeGk+4+6BTV04xKQhN1A470fScUf9O66Qp/NXk65ekT56iWUr/6HlLNvozyHysmPOF9ifEmAe4C7fBq3CdYGnuW/c0T+vYQkx0hP0sA0Dkx3Z9SzIoA/pdcx/uolGvxDKITdQaxdOq+lxWsMUEN9fL9aA7TuWnsrP2oujfvV8Tp797ZdJsf7lyT6Qwi/SBd/AVBLBwijdPZ9EgQAAFQNAABQSwECFAAUAAgACADJiDc8o3T2fRIEAABUDQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEwEAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br />
+|}
+'''<span style="color: blue">Erklärung:</span>''' <br />
+Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der rote Graph g liegt jeweils so viele Einheiten über bzw. unter dem Graphen f, wie der Regler anzeigt. <br />
+Man kann also sagen, dass der Graph g &nbsp; a Einheiten über dem Graphen f liegt. Das bedeutet bespielsweise für a=3, dass jeder Funktionswert g(x) an der Stelle x &nbsp; 3 Einheiten größer ist, als
+der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings <span style="color: blue">um a Einheiten nach oben (in positiver y-Richtung) bzw.
+nach unten (in negativer y-Richtung) verschoben</span>.  <br />
+:Für den Funktionsterm g(x) gilt somit: <span style="color: blue">g(x)=f(x)</span><span style="color: red">+a</span>.  <br /> <br />
+<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup>	<br />
+:::<span style="color: green">f(1)=1</span> <br />
+Verschiebung um <span style="color: red">3 Einheiten nach oben</span>   →  	 g(x)=f(x)+3	<br />
+::: g(1)=<span style="color: green">f(1)</span><span style="color: red">+3</span> <br />
+::: g(1)=<span style="color: green">1</span><span style="color: red">+3</span> <br />
+::: g(1)=4 </div> <br /> <br />
-'''<span style="color: blue">Erklärung:</span>''' Der Graph f gehört zu dem Funktionsterm f(x)=x<sup>3</sup>. Der Graph h liegt 3 Einheiten über dem Graphen f. Das bedeutet, dass jeder Funktionswert h(x) an der Stelle x 3 Einheiten größer ist, als der Funktionswert f(x). Dies fällt auch auf, wenn man die Graphen im Koordinatensystem betrachtet. Der rote Graph h verläuft über dem Graphen f, nimmt aber ansonsten den gleichen Verlauf. Er ist also um <span style="color: red">3 Einheiten in positiver y-Richtung (nach oben)</span> verschoben. <br /> Für den Funktionsterm h(x) gilt somit: h(x)=f(x)<span style="color: red">+3</span>. <br /> <br />
-<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup>	<br /> 	<br /> <br />
-:::<span style="color: green">f(2)=8</span> <br />
-Verschiebung um <span style="color: red">3 Einheiten nach oben</span>   <math>\rightarrow</math>  	 h(x)=f(x)+3	<br />
-::: h(2)=<span style="color: green">f(2)</span><span style="color: red">+3</span> <br />
-::: h(2)=<span style="color: green">8</span><span style="color: red">+3</span> <br />
-::: h(2)=11 </div> <br /> <br />
+<div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> <span style="color: red">'''Merke:'''</span>''' <br />
-<div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> '''<span style="color: red">Merke:</span>''' <br />
+Bei zwei gegebenen Funktionen f und g, für die gilt: '''g(x)=f(x)'''<span style="color: red">+a</span> entsteht der Graph g durch eine Verschiebung des Graphen f um <span style="color: red">a</span> Einheiten in y-Richtung.'''  <br />
-Bei zwei gegebenen Funktionen f und h, für die gilt: h(x)=f(x)<span style="color: red">+a</span> entsteht der Graph h durch eine Verschiebung des Graphen f um <span style="color: red">a</span> Einheiten in y-Richtung. Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives 	a in negativer y-Richtung (nach unten).</div> <br /> <br /> <br /> <br />
+Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten). </div> <br /> <br /> <br /> <br />
 == <span style="color: blue">2.Verschiebung nach rechts/links</span> ==
-'''<span style="color: blue">Problemstellung:</span>''' Nun entsteht der Graph j, indem der Graph von f mit x→x<sup>3</sup>+2x<sup>2</sup> um 3 Einheiten nach rechts verschoben wird. Welcher Zusammenhang besteht nun zwischen den Funktionen?
+'''<span style="color: blue">Problemstellung:</span>''' <br />
-<ggb_applet width="892" height="512"  version="3.2" ggbBase64="UEsDBBQACAAIANeQMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZRj9M4EH6GX2H5iQVtm6RN25WaRRwnJKTleOgdSDwgOck0MXXsyHa66f76G9tJ2+0d0iLgyfZ4Mv7mm5mvXb/uG0H2oA1XMqPxJKIEZKFKLquMdnZ7vaKvb5+vK1AV5JqRrdINsxmdTRLq7B2/ff5sbWp1T5jwLp843GfU6g4oMa0GVpoawAbzlgmDdtb1XHCmDx/zb1BYc7oIMd7LtrNjkKIp77gZj1P/Xiu4/ZPveQmaCFVkdJEictx9Am15wURG51GwJBlNLi7RNHO3tdL8QUnr3E/Bt2ghxPAHQEISZ1tPfZ5r6ArBS86kS8bjQCdC7nlpa4QwW2BI4FWNWNM4CtEKpXS5ORgLDem/gFbu7ZXj+TCckqU7GcSFD6bLySJaLW7SRZrEy9lNjH7j1Xwyj+PlYr6M0tUqmaXhAdhvwFqslyGsBzOyVmlenu/fmz+UKI9Et4pL+5a1ttO+1LPBtLEH9xYC0i6RN7ISMNgQSlFDsctVvwnkzELovw+t/8TDyau3SihNtKM9RYdhzcPqfRzOo1fkfSLvMcRwQY/38U3iPfyah9V7CS4DtCHveEx6pJ713BBncPRih450CJYDVpySTnJ7Nx6wM3anTJ3/X12T42Sc98YxZPyLQq6nF0213oGWIELrSKxrpzpD9q5FQ+k8jhIK3uAxXAyEMFesfxBAsJZQaRhxh7kKdPnbR+15YV5PRxAOg0GshUV9wHysywXHyBQ1hxwk2aP5XSd37t5UmrU1SDffFmcro++whpgZ+czFjpKSWfzayQb0KAzGaU5gjmByKDx9i+uL/opkpP/6YjaJrsgrkkwi8tKdcXPl0YGABnBGre+7bSc9umMRtvRxd9gayyDxOUfU8NGQvdct5TXoopKnkuP1d3oV1aqtGe4mQzjBDqhH5/T6aB9U+Zh0JrF4nlGUhdYFcO3RApSDBI8gSYsh/Xye1f4JmWFXBY7+w5bsGtC8OOaZe7IQXDdAjCe/mJv4idwMfkZ4UW84/hxdp46MhvUofm7HcqNEZ2FTYGPLO1V4Ekd0gwzHkasHwW/mXlgP7qfAbba8h5MA/r/2P6lrfqZ8jypzMQUZrYYhqMIQ4CyQa5JfUfKEtq9+X9uPQv7Tjf+DrTs9Vx//Mzz8Dbn9F1BLBwj6ycu4WwMAALgIAABQSwECFAAUAAgACADXkDI8+snLuFsDAAC4CAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJUDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />  <br /> <br />
+Im untenstehenden Applet siehst du den Graphen f mit x→x<sup>3</sup>+2x<sup>2</sup> und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst. <br />
+Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauszufinden. <br /> <br />
+<ggb_applet width="733" height="503"  version="3.2" ggbBase64="UEsDBBQACAAIABuJNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZNb9s4ED23v4LgKWkRW7IsOwGsFP1AgQLp7sHdLtDDApQ0llhTpEBSjpxf3yEp2Y63C6Ro9kRyOBq+eTPz7NWbvhFkB9pwJTMaTyJKQBaq5LLKaGc3V9f0ze3LVQWqglwzslG6YTajyWRGnb3jty9frEyt7gkT3uUrh/uMbpgwQIlpNbDS1AD2kZ11PRec6f2f+XcorDlehCCfZNvhK1Z3aCua8o6b8Tj1D7aC2w98x0vQRKgio4sUoePuK2jLCyYyOo+CZZbR2dklmhJ3WyvNH5S0zv0YfIMWQgx/AGRk4WyrqU90BV0heMmZdMl4HOhEyD0vbZ3RZZJgSOBVjVjTKA7RCqV0ud4bCw3pv4FW+PZy4YjeD6fkxp0M4sIH0+VkEV0vbtJFOouXyU2MfuPVfDKP4+VivozS6+tZkoYHYLcGa7FghrAezMhapXl5uv9k3ilRHohuFZf2PWttp32tk8G0tnv3FgLSLpG3shIw2BBKUUOxzVW/DuQkIfSXfes/8XDy6r0SShPtaE/RYVjzsHofh/PgFXmfyHsMMVzQw318M/Mefs3D6r0ElwHakHcyJh1H4zPcEGdw9GKLjnQIlgNWnJJOcns3HrAztsdMnf8fXZPjaJz2xiFk/EwhV9OzplptQUsQoXUk1rVTnSE716KhdB5HCQVv8BguBkKYK9ZfCCBYS6g0jLjDXAW6/G102p5n5tV0BOEwGMRaWBQIzMe6XHCMTFFzyEGSHZo/dnLr7k2lWVuDdPNtcbYy+hFriJmRv7nYUlIyi1873YAehcE40QnMEUwOladvcb3oL0lG+n8ukkl0SV6T2SQir9wZN5ceHQhoAGfU+r7bdNKjOxRhQx93h62xDBKfQ02gw0dD9l64lNegs0oeS47X/9GrqFZtzXA3GcIJtkc9OqXXR/usysekM4nF84yiLLQugGuPFqAcNHgESVoM6efzpPZPyAy7KnD0L7Zk14DmxSHP3JOF4LoBYjx5Zm7iJ3Iz+BnhRb3h+Ht0lToyGtaj+Lkdy40SnYV1gY0t71ThSRzRDTIcR64eBL+ZL73Mup8Ct9nwHo4C+HPt/ym3s7Ou+Z3yParM2RRktBqGoApDgLNArkh+SckT2r76/9p+FPLfbvxfbN3pqfr4n+Hhf8jtD1BLBwhQD2hSYQMAALkIAABQSwECFAAUAAgACAAbiTc8UA9oUmEDAAC5CAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJsDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />  <br /> <br />
-'''<span style="color: blue">Erklärung:</span>''' Eine Verschiebung des Graphen <span style="color: red">um 3 Einheiten in positiver x-Richtung</span> (also nach rechts) bedeutet, dass der Graph j 3 Einheiten weiter rechts verläuft, als der Graph f. Somit entspricht der Funktionswert von f an der Stelle x dem Funktionswert von j an der Stelle x+3.<br />  Somit ergibt sich der Zusammenhang j(x)=f(<span style="color: red">x-3</span>). <br /> <br />
+'''<span style="color: blue">Erklärung:</span>''' <br />
+Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben <br />
+nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings <span style="color: blue">um b Einheiten nach rechts bzw. links verschoben</span>. Somit entspricht <br />
+der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.<br />
+Das bedeutet für den funktionellen Zusammenhang: <span style="color: blue">g(x)=f</span>(<span style="color: red">x-3</span><span style="color: blue">)</span>. <br /> <br />
 <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>'''	f(x)=x<sup>3</sup>+2x<sup>2</sup>  <br />
-:::x=1 <math>\rightarrow</math>  f(1)=3   <br />    <br />
+:::x=1 →   f(1)=3   <br />    <br />
 	Verschiebung um <span style="color: red">3 Einheiten nach rechts</span>: <br />
-:::j(x)=f(x<span style="color: red">-3</span>) <br />
+:::g(x)=f(x<span style="color: red">-3</span>) <br />
-:::j(x)=(x-3)<sup>3</sup>+2(x-3)<sup>2</sup> <br />
+:::g(x)=(x-3)<sup>3</sup>+2(x-3)<sup>2</sup> <br />
-:::j(4)=(4-3)<sup>3</sup>+2(4-3)<sup>2</sup> <br />
+:::g(4)=(4-3)<sup>3</sup>+2(4-3)<sup>2</sup> <br />
-:::<span style="color: green">j(4)</span>=1+2=3=<span style="color: green">f(1)</span> </div> <br /> <br />
+:::<span style="color: green">g(4)</span>=1+2=3=<span style="color: green">f(1)</span> </div> <br /> <br />
-Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von j(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist. <br /> <br />
+Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von g(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist. <br /> <br />
 <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; ">'''<span style="color: red">Merke:</span>''' <br />
-Bei zwei gegebenen Funktionen f und j, für die gilt: j(x)=f(x<span style="color: red">-b</span>) entsteht der Graph j durch eine Verschiebung um <span style="color: red">b</span> Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).</div>
+Bei zwei gegebenen Funktionen f und g, für die gilt: '''g(x)=f(x'''<span style="color: red">-b</span>''')''' entsteht der Graph j durch eine Verschiebung um <span style="color: red">b</span> Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links). </div>
+<br /> <br />
 == <span style="color: blue">3.Beispielaufagben</span> ==
-''' <span style="color: blue">Aufgabe 1:</span>''' <br /> Gegeben ist die Funktion f(x)=x<sup>3</sup>+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.
+<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>''' <br /> Gegeben ist die Funktion f(x)=x<sup>3</sup>+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.
@@ Zeile 54: / Zeile 79: @@
 ::=x<sup>3</sup>-4x<sup>2</sup>+4x-2x²+8x-8+5x-20 <br />
 ::='''x<sup>3</sup>-6x<sup>2</sup>+17x-28'''
-</popup>
+</popup> </div>
-''' <span style="color: blue">Aufgabe 2:</span>''' <br /> Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x<sup>3</sup> hervorgegangen sind.
+<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 2:</span>''' <br /> Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x<sup>3</sup> hervorgegangen sind.
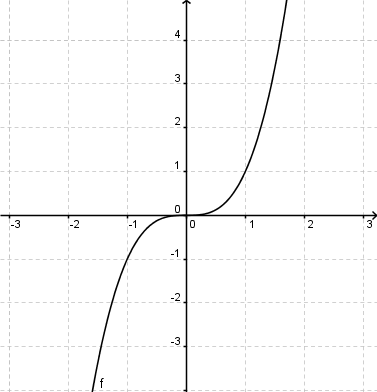
 Ausgangsfunktion: <br />
-[[Bild:Aufgabe 2 Verschiebungen 1.png|400px]] <br /> <br />
+[[Bild:Aufgabe 1.2 Verschiebungen 1.png|400px]] <br /> <br />
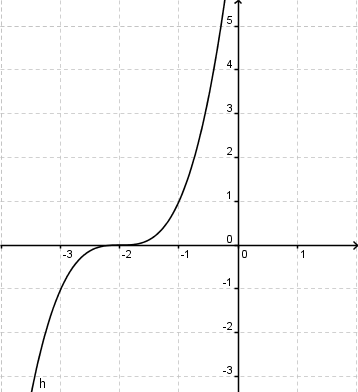
-a) [[Bild:Aufgabe 2 Verschiebungen 2.png|400px]] b) [[Bild:Aufgabe 2 Verschiebungen 3.png|400px]] c) [[Bild:Aufgabe 2 Verschiebungen 4.png|400px]] <br /> <br />
+a) [[Bild:Aufgabe 1.2 Verschiebungen 2.png|400px]] <br /> <br />
+b) [[Bild:Aufgabe 1.2 Verschiebungen 3.png|400px]] <br /> <br />
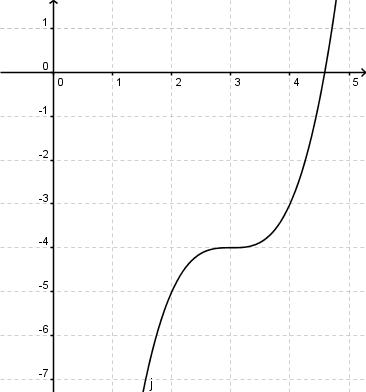
+c) [[Bild:Aufgabe 1.2 Verschiebungen 4.png|400px]] <br /> <br />
@@ Zeile 82: / Zeile 111: @@
 :::j(x)=x<sup>3</sup>-6x<sup>2</sup>+9x-3x<sup>2</sup>+18x-27-4 <br />
 :::'''j(x)=x<sup>3</sup>-9x<sup>2</sup>+27x-31'''
-</popup> <br /> <br />
+</popup> </div> <br /> <br />
-''' <span style="color: blue">Aufgabe 3:</span>''' <br />
+<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 3:</span>''' <br />
 Kreuze an, was stimmt. Es können mehrere Antwortmöglichkeiten richtig sein. <br /> <br />
 <quiz display="simple">
@@ Zeile 117: / Zeile 146: @@
 - nach unten
-</quiz>
+</quiz> </div>
+|} <br />
 [[Facharbeit Florian Wilk/Strecken und Spiegeln von Funktionsgraphen|Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen]]

Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen

Aktuelle Version vom 27. Januar 2010, 15:59 Uhr

Inhaltsverzeichnis

Verschieben von Funktionsgraphen

1.Verschiebung nach oben/unten

2.Verschiebung nach rechts/links

3.Beispielaufagben

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Hilfen

Oberstufe

Studien- und Berufsorientierung am RMG

Werkzeuge