Teilaufgabe b: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (Schützte „Facharbeit Andre Etzel/Teilaufgabe b“: Facharbeit [edit=sysop:move=sysop] [kaskadierend]) |
|||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | :1. Geben Sie aufgrund Ihrer Ergebnisse aus Teilaufgabe a)zwei Eigenschaften des Graphen einer Stammfunktion von | + | :1. Geben Sie aufgrund Ihrer Ergebnisse aus Teilaufgabe a) zwei Eigenschaften des Graphen einer Stammfunktion von <math>f_a\,</math> an! |
| − | :2. Bestimmen Sie durch partielle Integration eine Gleichung einer Stammfunktion von | + | :2. Bestimmen Sie durch partielle Integration eine Gleichung einer Stammfunktion von <math>f_a\,</math>! |
| − | :3. Die x-Achse und der Graph der Funktion | + | :3. Die x-Achse und der Graph der Funktion <math>f_2\,</math> begrenzen im I. Quadranten eine nach rechts ins Unendliche reichende Fläche. Berechnen sie deren Inhalt! |
::Hinweis: <math>\lim_{x\to\infty}x\cdot e^{-x} = 0 </math> | ::Hinweis: <math>\lim_{x\to\infty}x\cdot e^{-x} = 0 </math> | ||
[[Facharbeit Andre Etzel/Teilaufgabe b/Lösung von Teilaufgabe b|Lösung von Teilaufgabe b)]] | [[Facharbeit Andre Etzel/Teilaufgabe b/Lösung von Teilaufgabe b|Lösung von Teilaufgabe b)]] | ||
Aktuelle Version vom 30. Januar 2010, 10:19 Uhr
- 1. Geben Sie aufgrund Ihrer Ergebnisse aus Teilaufgabe a) zwei Eigenschaften des Graphen einer Stammfunktion von
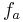 an!
an!
- 2. Bestimmen Sie durch partielle Integration eine Gleichung einer Stammfunktion von
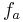 !
!
- 3. Die x-Achse und der Graph der Funktion
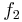 begrenzen im I. Quadranten eine nach rechts ins Unendliche reichende Fläche. Berechnen sie deren Inhalt!
begrenzen im I. Quadranten eine nach rechts ins Unendliche reichende Fläche. Berechnen sie deren Inhalt!
- Hinweis:
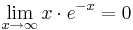
- Hinweis:

