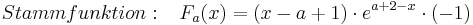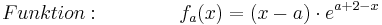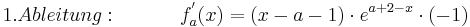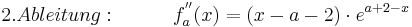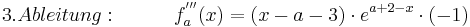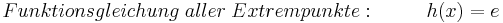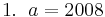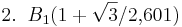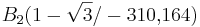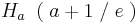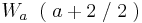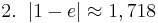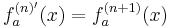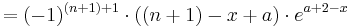Lösungsübersicht: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: == Funktion == Stammfunktion: <math> F_a (x) = ( x - a + 1 )\cdot (-e^{a + 2 - x}) </math> <br /> Funktion: <math> y = f_a (x) = ( x - a )\cdot e^{a + 2 - x}...)
 
(→‎Teilaufgabe a))
 
(21 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
== Funktion ==
 
== Funktion ==
  
−
Stammfunktion:     <math> F_a (x) = ( x - a + 1 )\cdot (-e^{a + 2 - x}) </math> <br />
+
:<math>Stammfunktion:    \;\;\; F_a (x) = ( x - a + 1 )\cdot e^{a + 2 - x}\cdot (-1) </math> <br />
−
Funktion:     <math> y = f_a (x) = ( x - a )\cdot e^{a + 2 - x} </math> <br />
+
 
−
1. Ableitung:     <math> f^{'}_a (x) = ( x - a - 1 )\cdot (-e^{a + 2 - x}) </math> <br />
+
:<math>Funktion:    \;\;\;\;\;\;\;\;\;\;\;\;\;\; f_a (x) = ( x - a )\cdot e^{a + 2 - x} </math> <br />
−
2. Ableitung:     <math> f^{''}_a (x) = ( x - a - 2 )\cdot e^{a + 2 - x} </math> <br />
+
 
−
3. Ableitung:     <math> f^{'''}_a (x) = ( x - a - 3 )\cdot (-e^{a + 2 - x}) </math> <br />
+
:<math>1. Ableitung:  \;\;\;\;\;\;\;\; \;\;\; f^{'}_a (x) = ( x - a - 1 )\cdot e^{a + 2 - x}\cdot (-1) </math> <br />
 +
 
 +
:<math>2. Ableitung:    \;\;\;\; \;\;\;\;\;\;f^{''}_a (x) = ( x - a - 2 )\cdot e^{a + 2 - x} </math> <br />
 +
 
 +
:<math>3. Ableitung:    \;\;\;\;\;\;\;\;\;\; f^{'''}_a (x) = ( x - a - 3 )\cdot e^{a + 2 - x}\cdot (-1) </math> <br />
 +
 
 +
Der Graph von <math>f_a(x)\,</math>
 +
<ggb_applet width="860" height="484"  version="3.2" ggbBase64="UEsDBBQACAAIAGW3NzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVfdb9s2EH9e/wpCT/YW2/q0JcBOsXV9KJB2Bbx1wB5W0NLZ5iKJAkklcv76HT8kO262Jksx5MEQdXc83v3ud0d5+bqrSnIDQjJer7xg6nsE6pwXrN6tvFZtJ6n3+vLVcgd8BxtByZaLiqqVF01DT8tbdvnqu6Xc81tCS2PyicHtylOiBY/IRgAt5B5AWfGWlhLltO1Yyag4/LL5C3Iljwrr413dtKp3klfFFZP968yc15RM/cxuWAGClDxfefMEI8fVJxCK5bRcebFvJeHKC4P4nhJFkdbuuWB3vFba/Oh8ixJCJLsDBCTUsuXM5LmENi9ZwWitkzFxoBEht6xQewwh1i6B7fYYa5yG1lvOuSjWB6mgIt0fIDiGE0bTIEnDLFr4KQY+98jBaaJkGmfJPM2yKMmSMEMIMV4MJIqmSZQlwTzzF4t0MU9wz1EVh1niJ3EUpME8WNiD4WYNSmEdJaEdyB7NnWDFALd+eSd/4uVR1HBWqze0Ua0wHIicaK0O+jBMUegMf6x3JThZiDXaQ3694d3aohZZ178eGrPFxLPZveElF0TghgTD37nnxj6NjQ50sPKNjW8snA/tdNAHWWgszHNjn8aqZLUNzSUe9FkHfn8Mk0QL0Lmmbo9NSTeAVPBIWzN11b8gZa5dpoG1/9BWG2yZU9IMLoNv5HI5O2Pb8hpEDaXlVI2FbXkryY3mri2diaOAnFX4ahUOEKqL9RsGYKUF7AT0cduGs3AZrX/K2zPxctYHoWOQGGuucHBgPkrnohtbYVPpVUGVluiuKaECbCll2FC3FQiWD8hQT5+GR7TuID2DZsNQ4WZAnKF5hB3V/8AXHCXNnuJqGjhW0AMOi9MUjbf3vOgPdseWZqpUDOfhJNEDsaLdyjMrupG8bBWscwSwvuI5VWZu2ujcHAh8X9t2esjoxQE3m8WWdXBstIeHz5G7ao8kqUFK02DqtJVojTU2wONYaWyOOGsBLP96W9JgzqaJB4Igq2w1vloXOK9LOF0EaZjqX5xkfpw8UCWX2v9RJgOmlZx0YX+v3Ffcy7rDO0nq664Pc/uZ4qXXNWY16sZkRUYdmRA6Jt8T+HNEyQ8knPoo6cYemX2B3LatTRd4pw4fXctvxXL/kfD5j+bZv6P2Ye1AG9ELgseP+73mtngIJ6c47n9u+ub6+K8AmPkmdZcGrklNj96dDCB77+kr3myMvg7K+uPnQw8Lursgk9EZi8ZPxcm4fCFI9eNsEuIqTZJonoX4zbGYz9PnIve2hw19IFLIKXgqUm9fCkyhg+nLiflMkH7/OPScZdOFodQTcUIvLwSoaADqiZ03O/36MN/n7v/J5d9QSwcI77bnGuwDAADRDAAAUEsBAhQAFAAIAAgAZbc3PO+25xrsAwAA0QwAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAAmBAAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
  
 
=== Teilaufgabe a) ===
 
=== Teilaufgabe a) ===
  
−
Nullstelle:                                 NS         ( a / 0 )
+
:<math>Nullstelle: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;NS \; ( \;a\;/ \;0 \;)\;</math>
−
Schnittpunkt mit der y-Achse:                SP<sub>y-Achse</sub> ( 0 / -a * e<sup>a + 2</sup>)
+
−
Extrempunkt:                                Max        ( 1 + a / e )
+
−
Wendepunkt:                                  WP        ( a + 2 / 2 )
+
 
   
 
   
−
  Funktionsgleichung aller Extrempunkte:       h (x) = e
+
:<math>Schnittpunkt\; mit \;der\; y-Achse: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;SP_{y-Achse} \;( \;0 \;/\; -a \cdot e^{a+2}\;)\;</math>
 +
   
 +
:<math>Extrempunkt:\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Max  \;  (\; 1 + a \;/\; e\; )\;</math>
 +
 +
:<math>Wendepunkt:  \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; WP \;    (\; a + 2 \;/ \;2 \;)\;</math>
 +
 +
:<math>Funktionsgleichung\; aller\; Extrempunkte: \;\;\;\;\;\;\;\;\;    h (x) = e\;</math>
  
 
=== Teilaufgabe b) ===
 
=== Teilaufgabe b) ===
  
−
1.
+
:<math>1.\;</math> Für <math>-\infty < x < a</math> ist der G<sub>F<sub>a</sub></sub> streng monoton fallend. <br />
−
  2. Stammfunktion:    <math> F_a (x) = ( x - a + 1 )\cdot (-e^{a + 2 - x}) </math> <br />
+
::  Für <math>a < x < \infty </math> ist der G<sub>F<sub>a</sub></sub> streng monoton steigend.<br />
−
3. Flächeninhalt zw. x-Achse und f<sub>2</sub>:    A = e<sup>2</sup>
+
::  Für <math>x = a\;</math> besitzt G<sub>F<sub>a</sub></sub> einen Tiefpunkt.<br />
−
 
+
   
 +
:<math>2.\;</math> Stammfunktion:    <math> F_a (x) = ( x - a + 1 )\cdot (-e^{a + 2 - x}) </math> <br />
 +
:<math>3.\;</math> Flächeninhalt zwischen der x-Achse und dem Graphen der Funktion f<sub>2</sub>:    <math>A = e^{2}\;</math>
  
 
=== Teilaufgabe c) ===
 
=== Teilaufgabe c) ===
  
−
  1. a = 2008
+
: <math>1.\;\;a = 2008\;</math>
−
  2. <math>B_1(1 + \sqrt{3} / 2,601)</math>
+
   
−
    <math> B_2(1 - \sqrt{3} / -310,164)</math>
+
: <math>2.\;\;B_1(1 + \sqrt{3} / 2{,}601)</math>
 +
 +
::  <math>\;\;\;\;\;\;\; B_2(1 - \sqrt{3} / -310{,}164)</math>
 +
 
  
  
 
=== Teilaufgabe d) ===
 
=== Teilaufgabe d) ===
  
 +
:<math>1.\;\;R_a \;\;(\; a\; /\; 0\; )\;</math><br />
 +
::<math>H_a \;\;(\; a + 1 \;/\; e\; )\;</math><br />
 +
::<math>W_a \;\;(\; a + 2 \;/\; 2 \;)\;</math><br />
 +
:Da sich die y-Werte dieser Punkte nicht verändern, haben diese immer denselben Abstand <br />  zueinander. Deshalb sind alle Dreiecke, die durch diese Punkte festgelegt sind, kongruent.
 +
 +
:<math>2. \;\;| 1 - e |  \approx 1,718</math>
  
  
  
 
=== Teilaufgabe e) ===
 
=== Teilaufgabe e) ===
 +
:<math>f_a^{(n)'}(x)= f_a^{(n+1)}(x)</math><br />
 +
 +
 +
::::<math>=(-1)^{(n+1)+1}\cdot((n+1)-x+a)\cdot e^{a+2-x}</math>
 +
 +
 +
 +
--[[Benutzer:Andre Etzel|Andre Etzel]] 23:18, 22. Jan. 2010 (UTC)

Aktuelle Version vom 26. Januar 2010, 21:38 Uhr

Inhaltsverzeichnis

Funktion

Stammfunktion: \;\;\; F_a (x) = ( x - a + 1 )\cdot e^{a + 2 - x}\cdot (-1)
Funktion: \;\;\;\;\;\;\;\;\;\;\;\;\;\; f_a (x) = ( x - a )\cdot e^{a + 2 - x}
1. Ableitung: \;\;\;\;\;\;\;\; \;\;\; f^{'}_a (x) = ( x - a - 1 )\cdot e^{a + 2 - x}\cdot (-1)
2. Ableitung: \;\;\;\; \;\;\;\;\;\;f^{''}_a (x) = ( x - a - 2 )\cdot e^{a + 2 - x}
3. Ableitung: \;\;\;\;\;\;\;\;\;\; f^{'''}_a (x) = ( x - a - 3 )\cdot e^{a + 2 - x}\cdot (-1)

Der Graph von 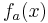f_a(x)\,

Teilaufgabe a)

Nullstelle: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;NS \; ( \;a\;/ \;0 \;)\;
Schnittpunkt\; mit \;der\; y-Achse: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;SP_{y-Achse} \;( \;0 \;/\; -a \cdot e^{a+2}\;)\;
Extrempunkt:\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Max \; (\; 1 + a \;/\; e\; )\;
Wendepunkt: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; WP \; (\; a + 2 \;/ \;2 \;)\;
Funktionsgleichung\; aller\; Extrempunkte: \;\;\;\;\;\;\;\;\; h (x) = e\;

Teilaufgabe b)

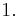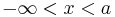1.\; Für -\infty < x < a ist der GFa streng monoton fallend.
Für 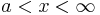a < x < \infty ist der GFa streng monoton steigend.
Für x = a\; besitzt GFa einen Tiefpunkt.
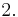2.\; Stammfunktion: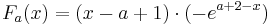 F_a (x) = ( x - a + 1 )\cdot (-e^{a + 2 - x})
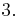3.\; Flächeninhalt zwischen der x-Achse und dem Graphen der Funktion f2: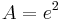 A = e^{2}\;

Teilaufgabe c)

1.\;\;a = 2008\;
2.\;\;B_1(1 + \sqrt{3} / 2{,}601)
\;\;\;\;\;\;\; B_2(1 - \sqrt{3} / -310{,}164)


Teilaufgabe d)

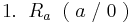
1.\;\;R_a \;\;(\; a\; /\; 0\; )\;
H_a \;\;(\; a + 1 \;/\; e\; )\;
W_a \;\;(\; a + 2 \;/\; 2 \;)\;
Da sich die y-Werte dieser Punkte nicht verändern, haben diese immer denselben Abstand
zueinander. Deshalb sind alle Dreiecke, die durch diese Punkte festgelegt sind, kongruent.
2. \;\;| 1 - e | \approx 1,718


Teilaufgabe e)

f_a^{(n)'}(x)= f_a^{(n+1)}(x)


=(-1)^{(n+1)+1}\cdot((n+1)-x+a)\cdot e^{a+2-x}


--Andre Etzel 23:18, 22. Jan. 2010 (UTC)

Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Lösungsübersicht&oldid=28322“