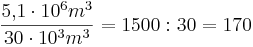BMT10 2008: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Aufgabe 1 Der größte Gletscher Bayerns, der Nördliche Schneeferner im Zugspitzgebiet, hat ein Volumen von 5,1 Millionen Kubikmetern und bedeckt eine Fläche von 30 ...)
 
 
(6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Aufgabe 1
+
__NOTOC__
 +
== '''Aufgabe 1'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 +
[[Bild:Zugspitzgletscher HQ.jpg|left|500px]]
  
 
Der größte Gletscher Bayerns, der Nördliche Schneeferner im Zugspitzgebiet, hat ein Volumen von 5,1 Millionen Kubikmetern und bedeckt eine Fläche von 30 ha. An einem heißen Tag verliert er 30000 m3 Eis durch Schmelzen und Verdunstung. Näherungsweise kann man davon ausgehen, dass sich dieser Verlust an Eis gleichmäßig über die gesamte Gletscherfläche verteilt.
 
Der größte Gletscher Bayerns, der Nördliche Schneeferner im Zugspitzgebiet, hat ein Volumen von 5,1 Millionen Kubikmetern und bedeckt eine Fläche von 30 ha. An einem heißen Tag verliert er 30000 m3 Eis durch Schmelzen und Verdunstung. Näherungsweise kann man davon ausgehen, dass sich dieser Verlust an Eis gleichmäßig über die gesamte Gletscherfläche verteilt.
 +
  
 
a) Wie viele heiße Tage müssten aufeinander folgen, bis der Gletscher unter den oben beschriebenen Bedingungen vollständig verschwunden ist?
 
a) Wie viele heiße Tage müssten aufeinander folgen, bis der Gletscher unter den oben beschriebenen Bedingungen vollständig verschwunden ist?
 +
 +
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:<math>\frac{5{,}1 \cdot 10^6m^3}{30 \cdot10^3 m^3}=1500:30 =170</math>
 +
 +
 +
}}
 +
</div>
  
 
b) Das Eisvolumen, das der Gletscher an einem heißen Tag verliert, soll durch einen Vergleich mit dem Volumen von Zimmern veranschaulicht werden. Geben Sie dazu sinnvolle Abmessungen eines Zimmers und die Anzahl dieser Zimmer an.
 
b) Das Eisvolumen, das der Gletscher an einem heißen Tag verliert, soll durch einen Vergleich mit dem Volumen von Zimmern veranschaulicht werden. Geben Sie dazu sinnvolle Abmessungen eines Zimmers und die Anzahl dieser Zimmer an.
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:z.B. 500 Zimmer mit 5 m Länge, 4 m Breite und 3 m Höhe
 +
:da 500 · 5 · 4 · 3 m³ = 30 000 m³
  
 +
}}
 +
</div>
 
c) Schätzen Sie durch Rechnung ab, um wie viele Zentimeter die Dicke des 30 ha großen Gletschers an einem heißen Tag durchschnittlich abnimmt.
 
c) Schätzen Sie durch Rechnung ab, um wie viele Zentimeter die Dicke des 30 ha großen Gletschers an einem heißen Tag durchschnittlich abnimmt.
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:30 000 m³ : 30 ha = 30 000 m³ : 300 000 m² = 0,1 m = 10cm
  
 +
}}
 +
</div>
 +
</div>
  
−
Aufgabe 2
+
== '''Aufgabe 2'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
Vereinfachen Sie die folgenden Terme jeweils so weit wie möglich.
 
Vereinfachen Sie die folgenden Terme jeweils so weit wie möglich.
 +
a)
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:*
 +
}}
 +
</div>
  
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:*
 +
}}
 +
</div>
  
−
Aufgabe 3
+
<div style="padding:1px;background:#ddeeff;border:1px groove;">
−
 
+
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:*
 +
}}
 +
</div>
 +
</div>
  
 +
== '''Aufgabe 3a''' ==
 +
<div class="multiplechoice-quiz">
 
a) Nebenstehende Skizze zeigt ein Steigungsdreieck mit der Steigung dh und dem Neigungswinkel α. Markieren Sie die richtige Beziehung für dieses Dreieck.
 
a) Nebenstehende Skizze zeigt ein Steigungsdreieck mit der Steigung dh und dem Neigungswinkel α. Markieren Sie die richtige Beziehung für dieses Dreieck.
 +
(!2023)  (!2023)  (!2023)  (2222) (!1987) (!14912)
 +
</div>
  
−
c) Welcher der folgenden Terme gibt an, wie viele Meter man auf der unteren Rossfeldstraße zurücklegen müsste, um einen Höhenunterschied von 100 m zu erzielen?
 
  
−
Aufgabe 4
+
==''' Aufgabe 3b''' ==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 +
Im unteren Teil hat die Straße von Berchtesgaden zum Rossfeld eine Steigung von 25 %.
 +
 
 +
Zeigen Sie, dass die Steigung von 25 % im abgebildeten Verkehrsschild nicht richtig dargestellt ist. Messen Sie dazu geeignete Strecken in einem Steigungsdreieck. Machen Sie im Bild kenntlich, welche Strecken Sie abgemessen haben.
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:*
 +
}}
 +
</div>
 +
</div>
 +
 
 +
== '''Aufgabe 3c''' ==
 +
<div class="multiplechoice-quiz">
 +
Welcher der folgenden Terme gibt an, wie viele Meter man auf der unteren Rossfeldstraße zurücklegen müsste, um einen Höhenunterschied von 100 m zu erzielen?
 +
 
 +
(!2023)  (!2023) (!1987) (!14912) (2222)
 +
</div>
 +
 
 +
== '''Aufgabe 4'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
Aus einer Urne mit 6 roten und 4 blauen Kugeln werden nacheinander 2 Kugeln gezogen. Zu diesem Zufallsexperiment gehört das nachstehende Baumdiagramm.
 
Aus einer Urne mit 6 roten und 4 blauen Kugeln werden nacheinander 2 Kugeln gezogen. Zu diesem Zufallsexperiment gehört das nachstehende Baumdiagramm.
  
 
a) Berechnen Sie die Wahrscheinlichkeit, mit der zwei verschiedenfarbige Kugeln gezogen werden.
 
a) Berechnen Sie die Wahrscheinlichkeit, mit der zwei verschiedenfarbige Kugeln gezogen werden.
 +
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:*
 +
}}
 +
</div>
  
 
b) Wurde in diesem Zufallsexperiment mit oder ohne Zurücklegen gezogen? Begründen Sie Ihre Entscheidung anhand des Baumdiagramms.
 
b) Wurde in diesem Zufallsexperiment mit oder ohne Zurücklegen gezogen? Begründen Sie Ihre Entscheidung anhand des Baumdiagramms.
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:*
 +
}}
 +
</div>
 +
</div>
  
  
−
Aufgabe 5
 
−
Von einem Punkt P aus soll das Lot
 
−
auf eine Gerade g gefällt werden.
 
−
Nebenstehende Abbildung zeigt eine
 
−
mögliche Konstruktion.
 
−
Erklären Sie in Worten,
 
−
wie dabei vorgegangen wurde.
 
  
 +
==''' Aufgabe 5'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 +
Von einem Punkt P aus soll das Lot auf eine Gerade g gefällt werden.
 +
Nebenstehende Abbildung zeigt eine mögliche Konstruktion.
 +
Erklären Sie in Worten, wie dabei vorgegangen wurde.
  
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:
 +
}}
 +
</div>
 +
</div>
  
−
Aufgabe 6
+
 
 +
 
 +
==''' Aufgabe 6'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
Geben Sie einen möglichen Funktionsterm für die Funktion f bzw. g an, die die jeweils angegebene Eigenschaft haben soll. Eine Definitionsmenge braucht nicht angegeben zu werden; es wird die für den jeweiligen Term maximal mögliche vorausgesetzt.
 
Geben Sie einen möglichen Funktionsterm für die Funktion f bzw. g an, die die jeweils angegebene Eigenschaft haben soll. Eine Definitionsmenge braucht nicht angegeben zu werden; es wird die für den jeweiligen Term maximal mögliche vorausgesetzt.
  
−
a) Die Funktion f hat genau die zwei Nullstellen 3 und 0. f(x) = ...........................................
+
a) Die Funktion f hat genau die zwei Nullstellen 3 und 0. f(x) = ..............
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:
 +
}}
 +
</div>
  
 
b) Die Funktion g ist bei x = 2 nicht definiert. g(x) = ..........................................
 
b) Die Funktion g ist bei x = 2 nicht definiert. g(x) = ..........................................
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:
 +
}}
 +
</div>
 +
</div>
  
−
 
+
−
Aufgabe 7
+
== '''Aufgabe 7'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
Ein gerader Kreiszylinder hat die Höhe h und den Radius r.
 
Ein gerader Kreiszylinder hat die Höhe h und den Radius r.
 
a) Erklären Sie, wie man die Formel M =rh2πfür den Inhalt der Mantelfläche des Zylinders herleiten kann.
 
a) Erklären Sie, wie man die Formel M =rh2πfür den Inhalt der Mantelfläche des Zylinders herleiten kann.
 +
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:
 +
}}
 +
</div>
  
 
b) Für den Inhalt O der Oberfläche des Zylinders gilt demnach:      Lösen Sie diese Formel nach der Höhe h auf.
 
b) Für den Inhalt O der Oberfläche des Zylinders gilt demnach:      Lösen Sie diese Formel nach der Höhe h auf.
  
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:
 +
}}
 +
</div>
 +
</div>
  
−
Aufgabe 8
+
 
 +
 
 +
 
 +
== '''Aufgabe 8'''==
 +
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
[AB] ist der Durchmesser des Halbkreises mit Mittelpunkt M. C
 
[AB] ist der Durchmesser des Halbkreises mit Mittelpunkt M. C
 
Der Eckpunkt C des Dreiecks ABC liegt auf diesem Halbkreis.
 
Der Eckpunkt C des Dreiecks ABC liegt auf diesem Halbkreis.
 
Beweisen Sie den Satz des Thales, indem Sie mit Hilfe von Winkelbetrachtungen zeigen, dass .
 
Beweisen Sie den Satz des Thales, indem Sie mit Hilfe von Winkelbetrachtungen zeigen, dass .
 +
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
:
 +
:
 +
:
 +
}}
 +
</div>
 +
</div>

Aktuelle Version vom 12. September 2009, 16:36 Uhr

Aufgabe 1

Zugspitzgletscher HQ.jpg

Der größte Gletscher Bayerns, der Nördliche Schneeferner im Zugspitzgebiet, hat ein Volumen von 5,1 Millionen Kubikmetern und bedeckt eine Fläche von 30 ha. An einem heißen Tag verliert er 30000 m3 Eis durch Schmelzen und Verdunstung. Näherungsweise kann man davon ausgehen, dass sich dieser Verlust an Eis gleichmäßig über die gesamte Gletscherfläche verteilt.


a) Wie viele heiße Tage müssten aufeinander folgen, bis der Gletscher unter den oben beschriebenen Bedingungen vollständig verschwunden ist?


\frac{5{,}1 \cdot 10^6m^3}{30 \cdot10^3 m^3}=1500:30 =170

b) Das Eisvolumen, das der Gletscher an einem heißen Tag verliert, soll durch einen Vergleich mit dem Volumen von Zimmern veranschaulicht werden. Geben Sie dazu sinnvolle Abmessungen eines Zimmers und die Anzahl dieser Zimmer an.

z.B. 500 Zimmer mit 5 m Länge, 4 m Breite und 3 m Höhe
da 500 · 5 · 4 · 3 m³ = 30 000 m³

c) Schätzen Sie durch Rechnung ab, um wie viele Zentimeter die Dicke des 30 ha großen Gletschers an einem heißen Tag durchschnittlich abnimmt.

30 000 m³ : 30 ha = 30 000 m³ : 300 000 m² = 0,1 m = 10cm

Aufgabe 2

Vereinfachen Sie die folgenden Terme jeweils so weit wie möglich. a)

Aufgabe 3a

a) Nebenstehende Skizze zeigt ein Steigungsdreieck mit der Steigung dh und dem Neigungswinkel α. Markieren Sie die richtige Beziehung für dieses Dreieck. (!2023) (!2023) (!2023) (2222) (!1987) (!14912)


Aufgabe 3b

Im unteren Teil hat die Straße von Berchtesgaden zum Rossfeld eine Steigung von 25 %.

Zeigen Sie, dass die Steigung von 25 % im abgebildeten Verkehrsschild nicht richtig dargestellt ist. Messen Sie dazu geeignete Strecken in einem Steigungsdreieck. Machen Sie im Bild kenntlich, welche Strecken Sie abgemessen haben.

Aufgabe 3c

Welcher der folgenden Terme gibt an, wie viele Meter man auf der unteren Rossfeldstraße zurücklegen müsste, um einen Höhenunterschied von 100 m zu erzielen?

(!2023) (!2023) (!1987) (!14912) (2222)

Aufgabe 4

Aus einer Urne mit 6 roten und 4 blauen Kugeln werden nacheinander 2 Kugeln gezogen. Zu diesem Zufallsexperiment gehört das nachstehende Baumdiagramm.

a) Berechnen Sie die Wahrscheinlichkeit, mit der zwei verschiedenfarbige Kugeln gezogen werden.

b) Wurde in diesem Zufallsexperiment mit oder ohne Zurücklegen gezogen? Begründen Sie Ihre Entscheidung anhand des Baumdiagramms.


Aufgabe 5

Von einem Punkt P aus soll das Lot auf eine Gerade g gefällt werden. Nebenstehende Abbildung zeigt eine mögliche Konstruktion. Erklären Sie in Worten, wie dabei vorgegangen wurde.


Aufgabe 6

Geben Sie einen möglichen Funktionsterm für die Funktion f bzw. g an, die die jeweils angegebene Eigenschaft haben soll. Eine Definitionsmenge braucht nicht angegeben zu werden; es wird die für den jeweiligen Term maximal mögliche vorausgesetzt.

a) Die Funktion f hat genau die zwei Nullstellen 3 und 0. f(x) = ..............

b) Die Funktion g ist bei x = 2 nicht definiert. g(x) = ..........................................


Aufgabe 7

Ein gerader Kreiszylinder hat die Höhe h und den Radius r. a) Erklären Sie, wie man die Formel M =rh2πfür den Inhalt der Mantelfläche des Zylinders herleiten kann.

b) Für den Inhalt O der Oberfläche des Zylinders gilt demnach: Lösen Sie diese Formel nach der Höhe h auf.



Aufgabe 8

[AB] ist der Durchmesser des Halbkreises mit Mittelpunkt M. C Der Eckpunkt C des Dreiecks ABC liegt auf diesem Halbkreis. Beweisen Sie den Satz des Thales, indem Sie mit Hilfe von Winkelbetrachtungen zeigen, dass .

Von „http://rmg.zum.de/index.php?title=BMT10_2008&oldid=19808“